Поняття випадкової величини

Поняття випадкової величини грає важливу роль у теорії статистичної радіотехніки, насамперед у зв'язку з тим, що дозволяє перейти від якісного опису характеристик випадкових подій до їхнього кількісного визначення.

Наприклад, подію, що складається у відмові радіостанції можна розглядати як випадкову величину , що дорівнює 1, якщо відмова відбувається, і дорівнює 0, якщо відмоване відбувається. У цьому випадку випадкова величина є скалярною й дискретною, приймаючою тільки два значення: 0 і 1.

Часто для обчислення ймовірності події виявляється зручним зв'язати її з якоюсь неперервною випадковою величиною (або системою неперервних величин), що приймає нескінченну кількість значень. Нехай, наприклад, виміряються координати повітряного судна, які відображаються на індикаторі наземної радіолокаційної станції. Подія 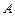полягає в тому, що похибка у визначенні місця знаходження повітряного судна не перевершить заданого значення 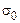. Для оцінки ймовірності 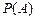запровадимо випадкові величини й , що характеризують похибки оцінки місця розташування по кожній із координатних площин. Очевидно, що для виконання події 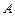повинна задовольнятися нерівність

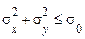Імовірність 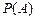у цьому випадку виражається через характеристики системи (вектора) двох неперервних випадкових величин і . Наведені приклади дозволяють дати загальне визначення випадкової величини.

Випадковою називається величина, яка у результаті досліду приймає те або інше значення, що заздалегідь передбачено бути не може.

Випадковою величиноюназивається числова функція, аргументом якої є наслідки випадкового досліду (події).

Співвідношення, що встановлює в тій або іншій формі залежність між можливими значеннями випадкової величини і їхніх ймовірностей, називається законом розподілу. Закон розподілу може бути заданий у формі ряду ймовірностей; функції розподілу або щільності ймовірності, кожна з яких забезпечує повний статистичний опис випадкової величини.

<== попередня сторінка	\|	наступна сторінка ==>
	\|

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.