Закон розподілу дискретної випадкової величини

Для опису дискретної випадкової величини використовуються ряд ймовірностей і функція розподілу.

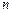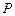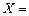
Позначимо дискретну випадкову величину через , а її можливі значення через . Поява кожного із цих значень можливе, але не вірогідне, тому величина може прийняти кожне з них із деякою ймовірністю. Позначимо відповідні ймовірності ( 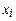) = . Оскільки розглянуті події несумісні й становлять повну групу, то сума ймовірностей всіх можливих значень випадкової величини дорівнює одиниці

Ця сумарна ймовірність розподілена між окремими значеннями певним чином, тому може бути заданий ряд розподілу.

Ряд розподілу дискретної випадкової величини можна задати графічно (рис. 1), у вигляді відповідної таблиці або аналітично у вигляді
( ) = .

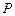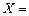
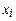Рис. 1. Графічне та табличне завдання ряду ймовірностей

Хоча ряд розподілу вичерпним образом описує випадкову величину, його застосування на практиці обмежено через труднощі, що виникають при описі великих масивів величин (наприклад, результатів тривалих експериментів). Більш зручною й розповсюдженою формою закону розподілу випадкової величини є функція розподілу.

Функцією розподілу випадкової величини називається функція 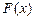, що визначає ймовірність того, що випадкова величина приймає значення, які менші 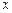(тобто з інтервалу від до ) :

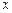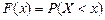. (1)

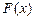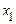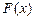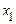Побудуємо функцію розподілу дискретної випадкової величини (рис. 2). Нехай імовірності окремих значень випадкової величини задані у вигляді графіка (рис. 1). Поки аргумент функції залишається менше , функція розподілу , дорівнює нулю, тому що немає жодного значення , що було б менше . У точці 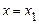відбувається розрив неперервності функції 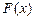. Її праве граничне значення дорівнює 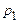, причому вона залишається постійною в інтервалі від 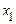до . У точці 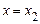функція 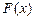знову терпить розрив неперервності. Тепер її праве граничне значення дорівнює 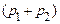. Дійсно, подія, що випадкова величина прийме значення, яке менше , де 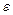> 0 – досить мале число, розпадається на дві неспільних події: прийняти з ймовірністю 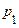значення 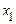й з ймовірністю 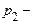значення .Аналогічним способом виконується побудова функції розподілу для інших значень 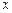. Коли поточна змінна 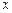проходить через яке-небудь із можливих значень дискретної величини , функція розподілу змінюється стрибкоподібно, причому величина стрибка дорівнює ймовірності цього значення.

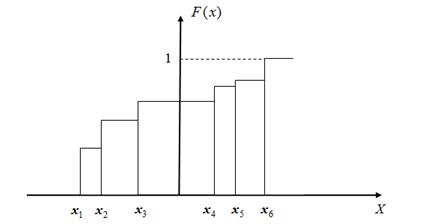
Рис. 2. Функція розподілу дискретної випадкової величини

Якщо загальне число можливих значень випадкової величини дорівнює 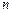, то

. (2)

Ця умова називається умовою нормування закону розподілу дискретної випадкової величини. Вона справедлива як для функції розподілу, так і для ряду ймовірностей.

Основні властивості функції розподілу.

1. Функція розподілу 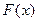є неспадаючою функцією свого аргументу, тобто при виконується .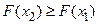

2. 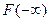= 0. Ця властивість відображає той факт, що немає значень випадкової величини , які були б менше, ніж негативна нескінченність.

3. 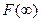= 1. Ця властивість відображає той факт, що подія, яка полягає в прийнятті випадковою величиною значення, меншого позитивної нескінченності, є подія достовірна.

Маючи у своєму розпорядженні всі значення ряду розподілу випадкової величини, легко побудувати функцію розподілу для фрагмента ряду (для заданого значення 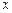). Дійсно,

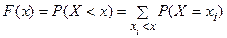де нерівність 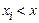під знаком суми вказує, що підсумовування розповсюджується на всі ті значення 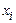, які менше .

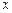<== попередня сторінка	\|	наступна сторінка ==>
	\|

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.