
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Нормальний закон розподілу
Нормальний закон розподілу (закон Гаусса) грає виняткову роль у задачах статистичної радіотехніки й займає особливе місце серед всіх законів розподілу випадкових величин насамперед через те, що в теорії ймовірностей доведено центральну граничну теорему, відповідно до якої щільність ймовірності суми рівномірно малих (граючих приблизно однакову роль) доданків при необмеженому збільшенні їхнього числа як завгодно близько наближається до нормальної щільності ймовірності, незалежно від того, які закони розподілу мають ці доданки. Крім того, з нормально розподілених (гауссівських) випадкових величин за допомогою відповідних перетворень можуть бути отримані випадкові величини з іншими щільностями ймовірності.
Щільність імовірності при нормальному (гауссівському) законі розподілу випадкової величини  задається виразом
задається виразом
 . (58)
. (58)
З виразу (58) видно, що максимальне значення 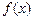 , що дорівнює
, що дорівнює  (рис. 8), досягається при
(рис. 8), досягається при  . При
. При 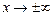 значення
значення 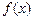 асимптотично прагне до нуля.
асимптотично прагне до нуля.
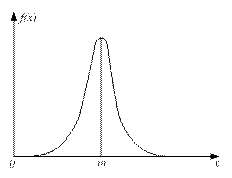
Рис.8. Нормальний закон розподілу випадкової величини
Нормальний закон розподілу випадкових величин повністю визначається параметрами 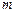 й
й  . З'ясуємо зміст цих параметрів і їхній зв'язок з основними числовими характеристиками нормального закону розподілу.
. З'ясуємо зміст цих параметрів і їхній зв'язок з основними числовими характеристиками нормального закону розподілу.
Обчислимо математичне сподівання гауссівської випадкової величини 
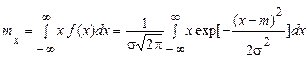 . (59)
. (59)
Введемо нову змінну 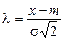 , тоді
, тоді 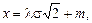
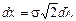 . Після підстановки в (59), отримуємо
. Після підстановки в (59), отримуємо

 .
.
Перший інтеграл в отриманій сумі дорівнює нулю через непарність підінтегральної функції, а другий – є відомим інтегралом Ейлера-Пуассона
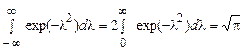 . (60)
. (60)
У підсумку для математичного сподівання гауссівської випадкової величини маємо
 .
.
Отриманий результат означає, що параметр 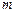 нормального закону розподілу (58) має сенс математичного сподівання гауссівської випадкової величини. З рис. 8 видно, що для розподілу (58) математичне сподівання збігається з модою й медіаною, а асиметрія дорівнює нулю, тому параметр
нормального закону розподілу (58) має сенс математичного сподівання гауссівської випадкової величини. З рис. 8 видно, що для розподілу (58) математичне сподівання збігається з модою й медіаною, а асиметрія дорівнює нулю, тому параметр 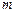 часто називають центром розсіювання гауссівської випадкової величини. При зміні значення параметра
часто називають центром розсіювання гауссівської випадкової величини. При зміні значення параметра 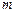 крива розподілу випадкової величини зміщається уздовж осі абсцис.
крива розподілу випадкової величини зміщається уздовж осі абсцис.
Обчислимо дисперсію гауссівської випадкової величини 
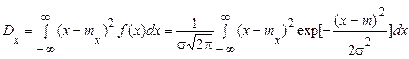 .
.
Використовуючи введену раніше нову змінну 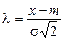 , отримаємо
, отримаємо
 .
.
Після інтегрування вроздріб
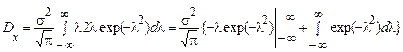 .
.
Перший доданок у фігурних скобках дорівнює нулю (при  співмножник
співмножник 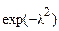 убуває швидше, ніж зростає співмножник
убуває швидше, ніж зростає співмножник 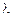 ), а другий доданок, що представляє інтеграл Ейлера-Пуассона, дорівнює
), а другий доданок, що представляє інтеграл Ейлера-Пуассона, дорівнює 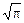 . У підсумку для дисперсії гауссівської випадкової величини
. У підсумку для дисперсії гауссівської випадкової величини  отримуємо
отримуємо
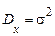 .
.
Це означає, що дисперсія випадкової величини  , розподіленої за нормальним законом з параметрами
, розподіленої за нормальним законом з параметрами 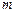 й
й  , дорівнює
, дорівнює 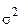 . Звідси слідує, що параметр
. Звідси слідує, що параметр  має сенс середнього квадратичного відхилення випадкової величини
має сенс середнього квадратичного відхилення випадкової величини 
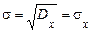 .
.
При зміні значення параметра  змінюється максимальне значення нормального закону розподілу, яке дорівює
змінюється максимальне значення нормального закону розподілу, яке дорівює  .
.
Оскільки площа під кривою розподілу завжди дорівнює одиниці, то зі зростанням  крива стає більш пологою (рис. 9), тобто збільшується розсіювання випадкової величини щодо центра розсіювання.
крива стає більш пологою (рис. 9), тобто збільшується розсіювання випадкової величини щодо центра розсіювання.
Визначимо ймовірність влучення гауссівської випадкової величини  на інтервал від
на інтервал від 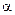 до
до 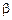
 .
.
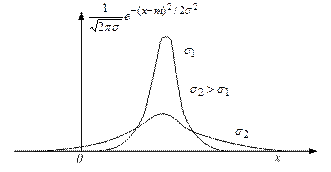
Рис.9. Графіки нормального закону для двох значень дисперсії
Після введення нової змінної 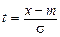 , отримаємо
, отримаємо
 . (61)
. (61)
Невизначений інтеграл виду 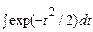 не виражається через елементарні функції, але може бути представлений через інтегральні функції, наприклад, через функцію
не виражається через елементарні функції, але може бути представлений через інтегральні функції, наприклад, через функцію
 ,
,
яка називається функцією Лапласа (інтегралом ймовірності) (рис. 10).
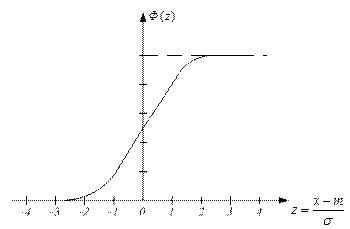
Рис.10. Графік інтегралу ймовірності
Часто в задачах радіотехніки більш зручним виявляється використання функції
 ,
,
яка називається нормальною функцією розподілу, оскільки являє собою функцію розподілу випадкової величини, що має щільність ймовірності (58) з параметрами  й
й  .
.
Нормальна функція розподілу 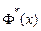 має наступні властивості:
має наступні властивості:
1. 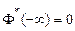 ;
;  ;
;
2.  .
.
Функція розподілу випадкової величини, що має нормальну щільність імовірності з параметрами 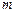 й
й  , просто виражається через нормальну функцію розподілу
, просто виражається через нормальну функцію розподілу
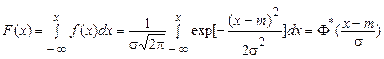 .
.
Звідси ймовірність влучення гауссівської випадкової величини  на інтервал від
на інтервал від 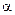 до
до 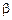
 . (62)
. (62)
Аргументи нормальної функції розподілу мають простий фізичний зміст:  являє собою відстань від
являє собою відстань від 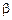 до центру розсіювання, нормовану до середнього квадратичного відхилення, а
до центру розсіювання, нормовану до середнього квадратичного відхилення, а 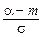 є така ж відстань від
є така ж відстань від 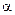 . Таким чином, нормальна функція розподілу
. Таким чином, нормальна функція розподілу  визначається параметрами
визначається параметрами 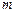 й
й  , які повністю описують закон розподілу гауссівської випадкової величини.
, які повністю описують закон розподілу гауссівської випадкової величини.
Центральний момент довільного порядку  для нормальної щільності розподілу записується у вигляді
для нормальної щільності розподілу записується у вигляді
 . (63)
. (63)
Використовуючи заміну 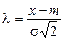 , отримаємо
, отримаємо
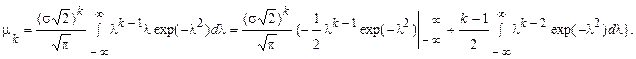
Перший доданок у фігурних дужках дорівнює нулю (для усіх значень  при
при  співмножник
співмножник  убуває швидше, ніж зростає співмножник
убуває швидше, ніж зростає співмножник 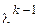 ), отже
), отже
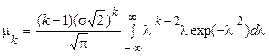 .
.
З (63) після заміни змінної слідує, що
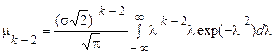 .
.
Остаточно маємо
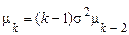 . (64)
. (64)
З врахуванням того, що
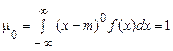 ,
,

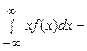
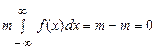 ,
,
формула (64) дозволяє виразити для нормального закону розподілу моменти вищих порядків через моменти нижчих порядків.
З рівності 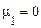 й (64) слідує, що всі інші центральні моменти непарного порядку також дорівнюють нулю. Це також безпосередньо випливає із симетричності нормального закону.
й (64) слідує, що всі інші центральні моменти непарного порядку також дорівнюють нулю. Це також безпосередньо випливає із симетричності нормального закону.
Для центральних моментів парного порядку може бути використане більш простий вираз, ніж (64), а саме
 , (65)
, (65)
де через  позначено добуток всіх непарних чисел від 1 до
позначено добуток всіх непарних чисел від 1 до 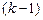 .
.
З (65) для четвертого моменту  , тому ексцес нормального закону розподілу
, тому ексцес нормального закону розподілу 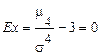 .
.
Нормальний закон розподілу поширюється й на векторні випадкові величини. Наприклад, дві випадкові величини  і
і  є спільно нормальними (спільно гауссівськими), якщо їхня спільна щільність імовірності має вигляд
є спільно нормальними (спільно гауссівськими), якщо їхня спільна щільність імовірності має вигляд
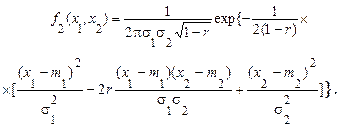 (66)
(66)
Окремі параметри (усього їх п'ять), що входять в (66), мають наступний сенс:  і
і 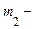 математичні сподівання випадкових величин
математичні сподівання випадкових величин  і
і 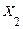 відповідно;
відповідно;  їх дисперсії;
їх дисперсії; 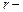 коефіцієнт кореляції, тобто
коефіцієнт кореляції, тобто
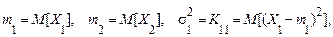

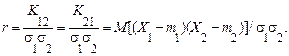
Шляхом інтегрування щільності ймовірності (66) по «зайвої» змінній неважко переконатися, що, якщо випадкові величини є спільно нормальними, то кожна з величин буде також нормальною. Зворотне твердження в загальному випадку невірно (воно завжди вірно тільки для незалежних випадкових величин).
З (66) слідує, що для некорельованих випадкових величин (  ) спільна щільність імовірності дорівнює добутку щільностей ймовірностей кожної з величин
) спільна щільність імовірності дорівнює добутку щільностей ймовірностей кожної з величин
 ,
,
де  .
.
Отже, якщо спільно нормальні випадкові величини некорельовані, то вони й незалежні. Тому для спільно нормальних випадкових величин некорельованість тотожна незалежності.
| <== попередня сторінка | | | наступна сторінка ==> |
| | |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |