
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Ортогональні проекції точки
ЗБІРКА ЗАДАЧ
з нарисної геометрії
для самостійної роботи студентів
напряму підготовки «Гірництво»
усіх форм навчання
Кривий Ріг – 2011
Укладачі: В.А. Дворніков, к.т.н., доцент,
В.С. Кравець, к.т.н., доцент,
О.П. Буршенко, викладач.
Відповідальний за випуск: В.А. Дворніков, к.т.н., доцент.
Рецензент: А.Н. Пижик, к.т.н., доцент.
У запропонованому збірнику наведено основні теоретичні положення та задачі з кожного розділу нарисної геометрії, розв’язання яких значно покращить якість самостійної роботи студентів. Збірник задач рекомендується для студентів професійного спрямування «Гірництво» усіх форм навчання
Розглянуто Схвалено
на засіданні кафедри вченою радою
нарисної геометрії та механіко-машинобудівного
інженерної графіки факультету
Протокол № 7 Протокол № 7
від « 21 » квітня 2011 від « 16 » травня 2011
ЗМІСТ
ВСТУП.. 3
1 Ортогональні проекції точки. 3
2 Ортогональні проекції прямої 3
3 Взаємне положення двох прямих. 3
4 Комплексне креслення площини. 3
5 Взаємне положення прямої та площини, двох площин. 3
6 Перетин двох площин, прямої та площини. 3
7 Перетворення ортогонального креслення. 3
8 Геометричні поверхні 3
9 Перетин поверхонь площиною та прямою.. 3
10 Взаємний перетин поверхонь. Розгортки. 3
11 Зображення: види, розрізи, перерізи, виносні елементи (ГОСТ 2.305-68) 3
12 Аксонометричні проекції 3
13 Проекції з числовими позначками. Пряма. Дві прямі 3
14 Проекції з числовими позначками. Площина. Взаємне положення двох площин, прямої та площини. 3
15 Топографічні поверхні 3
ЛІТЕРАТУРА.. 3
ВСТУП
Теоретичною основою інженерної графіки є нарисна геометрія, яка розглядає рішення математичних та інженерно-технічних задач за допомогою графічних методів. При цьому використовується метод проекціювання, який дозволяє отримати графічні зображення геометричних образів на три взаємно перпендикулярні площини проекцій П1, П2 і П3.
Найбільш поширеним є ортогональне, або прямокутне проекціювання. При такому проекцію ванні з будь-якої точки геометричного образу, який знаходиться у просторі, проводять перпендикуляри до перетину з П1, П2 та П3.
Таким чином отримують проекції різних точок, прямих, площин та інших геометричних елементів.
На основі аналізу проекцій, використання відповідних теоретичних положень та методик графічних побудов на кресленні отримують рішення вищезгаданих задач.
Для рішення кожної задачі необхідно:
1) вивчити відповідний теоретичний розділ курсу;
2) проаналізувати графічну умову задачі (визначити положення відносно П1, П2, П3 та основні властивості проекцій кожного геометричного образу);
3) розробити план рішення задачі, виходячи з умови мінімальної кількості графічних побудов;
4) записати алгоритм рішення (послідовність операцій) задачі;
5) виконати необхідні побудови.
При написанні алгоритму слід використовувати наступні позначення та символи:
1) площини проекцій – горизонтальна П1, фронтальна П2, профільна П3;
2) вісі проекцій – х, у, z;
3) позначення проекцій точок – горизонтальна А1, фронтальна А2, профільна А3;
4) проекції точки А на вісі проекцій – Ax, Ay, Az;
5) проекції відрізка прямої – А1В1, А2В2, А3В3;
6) h – горизонталь, f – фронталь, p – профільна пряма (прямі рівня);
7) прямі – a, b, c, d,…;
8) площини – А (альфа), Г (гамма), Δ (дельта), Σ (сигма), Θ (тета);
9) сліди площин – горизонтальний ГП1, фронтальний - ГП2 , профільний - ГП3;
10) належність - Ì, Î;
11) паралельність - ||;
12) перпендикулярність - ^;
13) дотичність – 
14) мимобіжність – 
15) співпадання - ≡;
16) пересічність - ∩, Х;
17) рівність, результат - =;
18) перетворення - ®;
19) еквівалентність – Û;
20) знак імплікації: якщо … , то … - Þ.
Ортогональні проекції точки
Механізм утворення проекції точки пояснює об’ємна модель (рис. 1). Для отримання проекцій точки А необхідно побудувати перпендикуляри до перетину з П1, П2, П3.
Точки перетину перпендикулярів з П1, П2, П3 визначають положення А1, А2, А3. Ax, Ay, Az – проекції точки А на вісі X, Y, Z.
На практиці використовують площинне креслення (епюр Монжа), яке отримують при суміщенні П1 та П3 з П2 за напрямком стрілок (рис. 2).
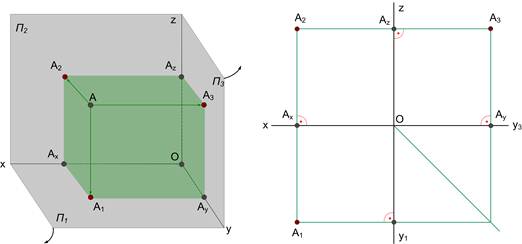
Рис. 1 Рис. 2
Основні властивості площинного креслення Монжа (рис. 2):
1) А2А1^Х; 2) А2А3^Z; 3) |A1AX|=|AZA3|=|AA2|.
1.1 Побудувати проекції точок за їх координатами:
А(10;20;30); В(15;25;0); С(0;30;35); D(20;0;40);
E(25;0;0); F(0;35;0); K(0;0;0).
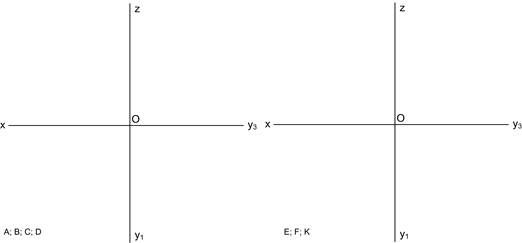
1.2 Побудувати проекції точки А` симетрично точці А відносно площини П1.
1.3 Побудувати проекції L за координатами L(15;-20;30).
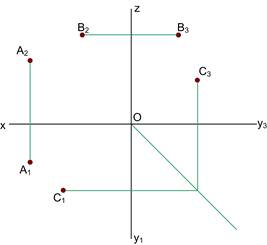
1.4 Побудувати відсутні проекції точок
| <== попередня сторінка | | | наступна сторінка ==> |
| Марківські випадкові процеси | | | Ортогональні проекції прямої |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |