• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Лекція 2. Графічні методи зображення статистичного матеріалу

Із метою наочності статистичний матеріал зображають графічно у вигляді: полігону, гістограми, кумуляти, емпіричної функції розподілу.

Полігон застосовується більше для зображення дискретного статичного ряду. Для його побудови у прямокутній системі координат наносять точки з координатами (x1; m1), (x2; m2), …, (xk; mk) або (x1; Q1), (x2; Q2), …, (xk; Qk) і з’єднують між собою прямими лініями. Отримана ламана буде полігоном частот (для першого ряду точок) або полігоном відносних частот (для другого ряду точок).

На рис. 2.1 зображено полігон частот, який відповідає статистичному ряду, поданому таблицею 2.1.

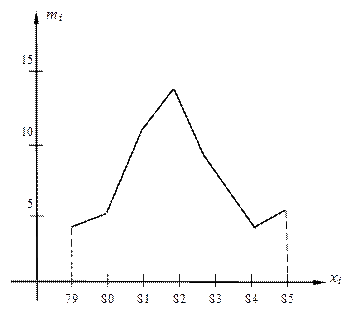
Рис. 2.1

Гістограмою зображають інтервальний статистичний ряд. Це східчаста фігура у вигляді прямокутників, що прилягають один до одного. Щоб побудувати гістограму, треба на осі абсцис прямокутної системи координат відкладати інтервали значень ознаки і на них, як на основах, побудувати прямокутники з висотами, пропорційними частотам (або відносним частотам інтервалів).

Гістограму частот, яка відповідає ряду, поданому таблицею 1.2, зображено на рис. 2.2.

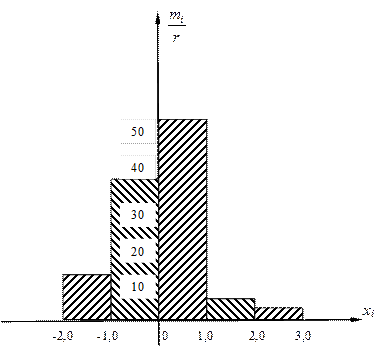
Рис. 2.2

Висота кожного прямокутника на гістограмі частот дорівнює відношенню 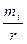(r – довжина інтервалу). Тоді площа кожного прямокутника 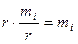дорівнює сумі частот варіант i-го інтервалу, а площа всієї гістограми частот дорівнюватиме сумі всіх частот, тобто обсягу вибірки.

Якщо побудувати гістограму відносних частот, тоді площа кожного прямокутника 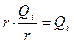дорівнює відносній частоті варіант, які потрапили на
i-й інтервал, а площа гістограми – сумі всіх відносних частот, тобто одиниці.

Кумулята (кумулятивна крива), або крива сум зображає статистичний ряд із нагромадженими частотами (відносними частотами).

Якщо розподіл є дискретним, то в прямокутній системі координат будуємо точки, абсцисами яких є варіанти, а ординатами – відповідні їм нагромаджені частоти або відносні частоти.

на рис. 3.3 зображена кумулята, яка відповідає ряду, поданому таблицею 3.1.

Якщо розподіл є неперервним, тоді відкладаємо точки, абсцисами яких є праві межі інтервалів, а ординатами – відповідні їм нагромаджені частоти. Крім цього, відкладаємо на осі абсцис точку, яка відповідає початку першого інтервалу (частота її дорівнює нулеві).

Рис. 2.3

З’єднавши отримані точки відрізками, отримаємо кумулятивну криву (криву зростаючих сумувань).

Графічне зображення емпіричної функції розподілу показано на рис.2.4 для середин інтервалів неперервного ряду, поданого таблицею 2.2. Значення функції F*(x) містяться в таблиці 2.3.

Таблиця 2.3

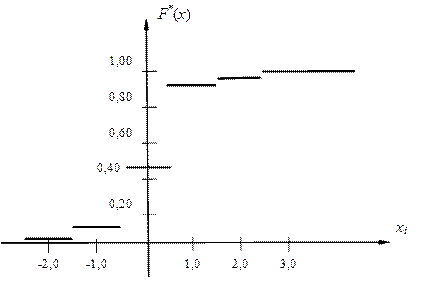
Рис.2.4

Побудова статистичного ряду – це перший крок до осмислення спостережень. Однак на практиці цього буває недостатньо, особливо коли виникає необхідність порівнювати ряди спостережень. Такі ряди можуть бути однотипними за формою при графічному зображенні, але відрізнятися значенням ознаки, відносно якої групуються результати спостережень, або мірою розсіювання, тобто певними кількісними характеристиками.

Відзначимо, що для будь-якого розподілу вибірки можна обчислити всі характеристики, а саме положення центра групування, розсіювання, асиметрію, ексцес і т.д. Ці характеристики називають емпіричними або вибірковими, оскільки вони отримуються зі спостережень і змінюватимуться від вибірки до вибірки.

Переглядів: 1046