Означення функції корисності. Аксіоматика щодо корисності за Нейманом–Моргенштерном.

Теорія Неймана-Моргенштерна є розвитком неокласичної теорії вибору рішень на випадок ризику. Рішення суб’єкта полягає у виборі найкращої з доступних альтернатив, кожна з яких в умовах ризику може бути охарактеризована не єдиним значенням, а ймовірносним розподілом багатства, який людина отримує при виборі даного рішення. Наприклад, нехай - множина всіх можливих значень добробуту (обсягів багатства), може отримати індивід в результаті рішення, яке він приймає. Будь-який варіант рішення може бути охарактеризований розподілом імовірностей Р, який характеризує ймовірність отримання кожного можливого рівня багатства. Нейман та Моргенштерн виходили з припущення, що людина приймає рішення раціонально, а її вподобання відповідають стандартним неокласичним аксіомам щодо поведінки людей. Це означає існування функції корисності, визначеної на множині ймовірносних розподілів, яка визначає вибір людини - найкраще для людини рішення дає найбільше значення функції корисності.

Крім того, Нейман та Моргенштерн ввели додаткове припущення - про незалежність (т.зв. лінійність) вподобань. Це означає - якщо, наприкад, рішення 1краще в очах людини за рішення 2, то і будь-яка комбінація рішення 1з деяким рішенням 3буде кращою за таку саму комбінацію рішень 2і 3. Наявність аксіоми незалежності дозволяє обгрунтувати конкретний вигляд функції корисності, приймаючи рішення людина вибирає найбільшу сподівану корисність результату.

Несхильна до ризику людна завжди надає перевагу рішенню з гарантованим виграшем перед ризикованим рішенням з таким самим сподіваним виграшем.

Різницю між сподіваним (середнім) виграшем ризикового рішення і еквівалентним цьому ризиковому рішенню (з точки зору людини) гарантованим виграшем називають премією за ризик, - це частина сподіваного виграшу, від якого несхильна до ризику людина готова відмовитись, щоб не ризикувати.

3. Теорема Неймана–Моргенштерна про існування функції корисності та її властивості як інтервальної функції цінності на множині лотерей (без доведення).

Власне так побудована функція корисності Дж.Неймана і О.Моргенштерна. Експерти пропонують порівнювати альтернативу: 1) значення показника х; 2) лотерею: одержати х* з імовірністю (1-р) чи х* з імовірністю (р). Величину ймовірності р змінюють доти, доки, на погляд експерта, значення показника х і лотерея L(x*, p, х* ) не стануть еквівалентними. Максимальному та мінімальному значенням х* та х* при-писують довільні числові значення U*=U(x*) та U*=U(x*), але так, щоб U*>U*.

Під лотереєю L(x*,p(х),х* ) розуміють ситуацію, в якій особа може отримати х* з імовірністю р(х) або х* з імовірністю 1-р(х).

Корисність варіанту х визначається ймовірністю р(х), при якій особі байдуже, що обирати х – гарантовано, чи лотерею L(x*,p(х),х* ), де х*,х* вектори, більш та менш пріоритетні порівняно з х.

Нехай L – лотерея, що приводить до виграшів (подій) х1,х2,…,хN з відповідними ймовірностями р1,р2,…, рN. Позначимо сподіваний виграш (математичне сподівання виграшу) через х:

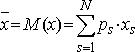
Справедлива головна формула теорії сподіваної корисності ,

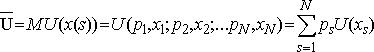
тобто корисність ансамблю результатів збігається з математичним сподіванням корисності результатів.

<== попередня сторінка	\|	наступна сторінка ==>
Поняття лотереї. Лотерея та її детермінований еквівалент. Премія за ризик.	\|	Висновки

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.02 сек.