Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Теоретичні відомості

Під математичною моделлю деякого елемента мається на увазі математична залежність, що приблизно описує зв'язок між вхідними і вихідними сигналами цього елемента. Існують різні способи визначення цих залежностей. Один з них заснований на аналізі статичних характеристик і перехідних функцій елемента.

Статична характеристика елемента встановлює зв'язок між сталими значеннями вхідного і вихідного сигналу елемента. Звичайно її представляють графіком чи у вигляді аналітичної залежності. Переважна більшість реальних елементів мають нелінійні статичні характеристики, тобто такі, котрі не можна представити на графіку у вигляді прямої лінії. Прикладом нелінійної статичної характеристики служить статична характеристика досліджуваного об'єкта, зображена на рисунку 1.1,а. Вхідним сигналом тут є напруга живлення U, а вихідним – температура θ.

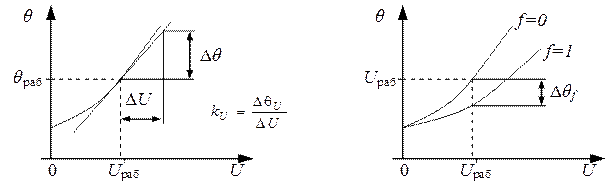
а) б)
Рисунок 1.1 – Обробка статичних характеристик об'єкта регулювання:
а) визначення коефіцієнта підсилення по керуючому впливі;
б) визначення коефіцієнта підсилення по збурюючому впливі.

Подібні характеристики, що не мають зламів і розривів, називаються несуттєво нелінійними. Якщо діапазон зміни вхідної і вихідної величин невеликий, то в цьому діапазоні статичну характеристику можна приблизно вважати лінійною. Заміна нелінійних характеристик лінійними, називається лінеаризацією. Тому що отримана лінійна залежність буде справедлива тільки для обмеженої ділянки статичної характеристики, то лінеаризоване рівняння (1.1) записують у відхиленнях від обраної робочої точки.

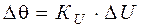, (1.1)

де , .

Отримане рівняння (1.1) є математичною моделлю статичних властивостей елемента в околиці робочої точки. Значення коефіцієнта підсилення k_U у цьому рівнянні дорівнює тангенсу кута нахилу дотичної до статичної характеристики в робочій точці і може бути визначене, як відношення відповідних збільшень вихідного і вхідного сигналів (див. рисунок 1.1, а) по формулі (1.2)

. (1.2)

Для елементів, що мають кілька вхідних сигналів, статичні властивості можуть бути представлені сімейством статичних характеристик. Так, наприклад, для досліджуваного об'єкта сімейство статичних характеристик буде складатися з двох кривих, що відповідають дії збурюючого впливу, (f = 1) і його відсутності (f = 0). При цьому коефіцієнт підсилення по збурюючому впливу у обраній робочій точці можна визначити по формулі (1.3), як відношення відхилення температури до приросту збурюючого впливу яке викликає це відхилення:

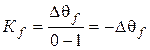. (1.3)

Перехідною функцією називається реакція елемента на одиничну східчасту функцію при нульових початкових умовах. Перехідна функція дає уяву про динамічні властивості елемента; часто по її вигляду можна записати диференціальне рівняння, що описує елемент. Для зняття перехідної функції на вхід елемента, що знаходиться в сталому режимі, потрібно подати стрибкоподібне збурювання і записати закон зміни вихідної величини (рисунок 1.2).

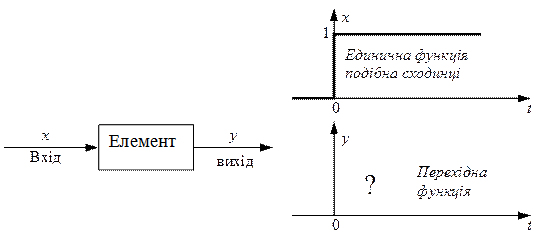
Рисунок 1.2 – Схема визначення перехідної функції елемента

Прикладами стрибкоподібних збурювань можуть служити миттєве зняття чи прикладення навантаження, ввімкнення чи вимкнення живильної напруги і т.д., тобто вхідний сигнал повинний бути стрибком змінений на деяку величину і потім залишатися постійним.

По своєму вигляду перехідні функції можуть бути найрізноманітнішими. Однак для наближеного опису динамічних властивостей елементів можна обмежитися порівняно невеликим набором типових динамічних моделей. Характеристики деяких з них приведені в таблиці 1.1.

Таблиця 1.1 – Характеристика деяких типових динамічних моделей

Назва моделі	Передаточна функція	Диференційне рівняння
1. Безінерційна ланка	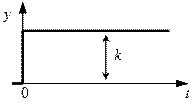k	y = k×x
2. Інерційна ланка	k/(T×р + 1)	T×dy/dt + y = k×x
3. Інтегральна ланка	k/p	dy/dt = k×x
4. Ланка затримки	е ^-pτ	y(t) = x×(t - τ)

Для теплових об'єктів перехідна функція, як правило, має вигляд, представлений на рисунку 1.3,а.

Рисунок 1.3 – Обробка перехідної функції теплового об'єкта:
а) реальна крива; б) ідеалізована крива.

Характер цієї кривої свідчить про досить складну динаміку нагрівання об'єкта. Для спрощення математичного опису криву трохи спрощують. Через точку перегину залежності проводять дотичну. При цьому перехідна функція розбивається на дві ділянки. На першій ділянці від 0 до моменту часу τ зміна температури незначна і нею можна знехтувати (див. рисунок 1.3,б). На другій ділянці починається розігрів об'єкта, причому швидкість зміни температури зменшується в міру наближення до сталого режиму. Представивши в такий спосіб перехідну функцію, динамічні властивості об'єкта можна описати, використовуючи послідовно дві моделі: ланка запізнювання та інерційну ланку. Час запізнення визначається величиною τ, а постійна часу Т дорівнює довжині проекції відрізка дотичної на вісь часу (див. рисунок 1.3,а). Величина коефіцієнта підсилення моделі залежить від вибору робочої точки і має бути визначена по статичній характеристиці об'єкта.

Математичні моделі САР прийнято зображувати у вигляді структурних схем, на яких окремі елементи системи зображуються у вигляді прямокутників з'єднаних стрілкою, що відображають зв'язки між елементами. Усередині прямокутників записують передаточні функції елементів. Передаточною функцією називається відношення зображення вихідного сигналу до зображення вхідного сигналу.

Перехідну функцію отримують виходячи з рішення результатів диференціального рівняння операторним методом при нульових початкових умовах. Наприклад, рівняння інерційної ланки (1.4)

, (1.4)

де y(t) – вихіднй сигнал;

x(t) – вхідний сигнал;

t – час;

k – коефіцієнт підсилення;

Т – постійна часу.

За допомогою перетворення Лапласа функції y(t), її похідних та правої частини диференційного рівняння задане диференційне рівняння (1.4) перетворюється у алгебраїчне (1.5)

, (1.5)

де p – оператор диференціювання, що заміняє d/dt ;

Y(p) – зображення вихідного сигналу;

X(р) – зображення вхідного сигналу.

Перетворивши рівняння (1.5) у (1.6)

, (1.6)

можна одержати вираз для передаточної функції інерційної ланки:

. (1.7)

При побудові математичної моделі об'єкта регулювання варто мати на увазі, що реальний об'єкт має два входи і його параметри по цих входах різні. Для того, щоб відобразити ці особливості, рекомендується зображувати структурну схему об'єкта так, як представлено на рисунок 1.4, де k_u, k_f – коефіцієнти підсилення по керуючому і збурюючому впливі, Т_u, τ_u – постійна часу і запізнювання по керуючому впливі; Т_f , τ_f – постійна часу і запізнювання по збурюючому впливі.

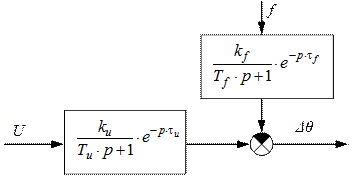
Рисунок 1.4 – Структурна схема досліджуваного об'єкта регулювання

<== попередня сторінка	\|	наступна сторінка ==>
Мета роботи	\|	Опис лабораторної установки

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.