Регулювальники з позиційним (релейним) законом регулювання.

Структурна схема позиційної системи авторегулювання (САР) наведена на рис. 1.

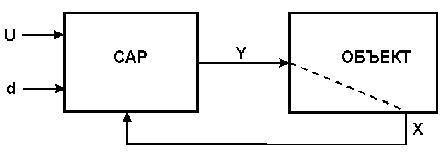
Рисунок 2.1 – Структурна схема САР:
U, d - вектора завдань і зон нечутливості;
X, Y - вектор регульованої величини і вихідний сигнал регулювання

Особливість таких регуляторів полягає в тому, що керуючий вплив (вихідний сигнал) приймає тільки кілька дискретних значень – позицій, тому їх називають позиційними. Даний тип регулятора ще називають Т-регулятором. Вони бувають з двопозиційним і трипозиційним законом регулювання.

Двопозиційні мають дискретну вихідну величину Y типа вкл./викл. (наприклад, включення/виключення нагрівача). Т-регулятора включає або вимикає вихідне реле залежно від того, досягла або не досягла регульована величина заданого значення.

Трипозиційні регулювальники мають дискретну вихідну величину Y з двома точками перемикання типа вкл./викл. і зоною нечутливості (наприклад, реверсивне управління сервоприводом) див. рис. 7,а.

Динамічні властивості об'єктів і вибір типа регулятора. Для визначення можливості використання Т-регулятора необхідно знати інерційність і час транспортного запізнювання регульованого об'єкту.

Для їх визначення на практиці найчастіше використовують методику зняття перехідної характерістіки, (див. лаб. работа №1).

Потрібний, щоб система знаходилася у спокої і були відсутні зовнішні обурення. На вхід виконавського органу подається ступінчаста дія 1(t) (рисунок 1.2)., внаслідок чого станом об'єкту є деякий процес X(t) – перехідну характеристику (див. на рисунку 2.2,а.).

Рисунок 2.2 – Обробка перехідної функції теплового об'єкта:
а) реальна крива; б) ідеалізована крива,

На рисунку 2.2 наведені позначення: τ – час транспортного запізнювання;
T – постійна часу (час узгодження) визначається інерційністю об'єкту; X_yст – стале значення; R – нахил розгінної кривої dx/dt (макс. швидкість зміни Х)

По вигляду цього перехідного процесу об'єкти регулювання можна підрозділити на декілька основних категорій:

- об'єкти з малою інерційністю і без запізнювання (T < 5 мін),

- об'єкти з інерційністю і з малим запізнюванням (τ/T < 0,1).

Виходячи із співвідношення τ/T і вибирається тип регулятору. Слід пам’ятати, що Т-регулятори можна застосовувати тільки якщо τ/T < 0,1. Позиційні регулятори не вимагають налаштування і забезпечують при цьому співвідношенні малий відхід від заданої температури.

Наприклад, вони використовуються для регулювання температури води в баках, в пастеризаторах, для управління нагрівом печі Ш2ХПА-25 хлібозаводу, в сушильних камерах ЖБК, в саунах і ін.

Алгоритм регулювання для позиційних регуляторів визначається статичною характеристикою регулювальника: залежністю вихідного сигналу Y від вхідного Х (див. рисунок 2.3).

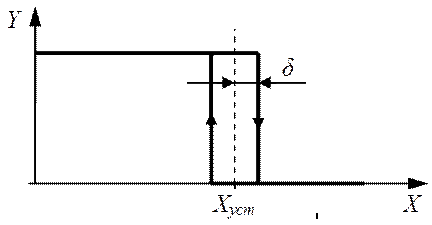
Рисунок 2.3 – Статична характеристика двопозиційного регулятора

Вихідна величина Y дорівнює максимальній дії (нагрівач включений) при
X – X_зад < – δ, Y = 0 при X – X_зад > δ, де δ – поріг. Таку характеристику ще називають гістерезисною, а поріг спрацювання регулятора гістерезисом.

Процесом регулювання є коливання навколо заданого рівня (див. рисунок 2.5). Частота і амплітуда коливань визначаються величинами τ, R, T, δ. Однак якщо параметри коливань задовольняють технологічним і експлуатаційним обмеженням, то система вважається працездатною.

Для об'єктів з великою інерційністю T і з малим запізнюванням τ регулювання відбувається з постійними коливаннями до 5-15% від U_зад. Чим більше δ, τ/T, R, тим більше амплітуда коливань. Чим більше τ і T, тим більше період коливань.

Розглянемо як приклад структурну схему досліджуваної в даній лабораторній роботі схему САР температури з двохпозиційним регулятором (рисунок 2.4).

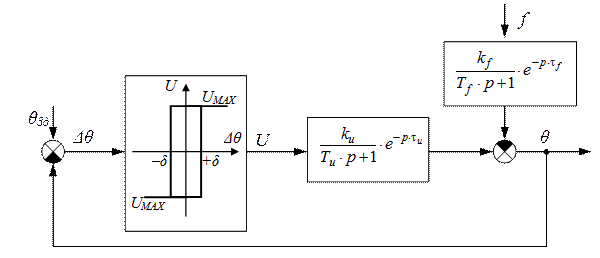
Рисунок 2.4 – Структурна схема САР температури з позиційним регулятором

Зображення об'єкта регулювання тут відповідає моделі, отриманої в роботі №1. Регулятор представлений статичною характеристикою двохпозиційного регулятора.

У вихідному стані температура об'єкта регулювання значно нижче заданої, сигнал неузгодженості має велике позитивне значення, тому на виході регулятора сигнал максимальний U і U_MAX і температура починає швидко збільшуватися (рисунок 2.5).

Рисунок 2.5 – Характер зміни температури і напруги живлення печі
при роботі позиційного регулятора

Коли температура перевищить задане значення на величину δ, регулятор спрацьовує і на виході його встановиться мінімальне значення керуючого впливу U = U_MIN. Однак, через запізнювання температура буде як і раніше збільшуватися і тільки через час τ почне зменшуватися.

Коли вона зменшиться нижче заданого на величину δ, регулятор знову спрацьовує і на виході установиться максимальне значення керуючого впливу U = U_MАХ. Але зниження температури буде ще продовжуватися в інтервалі часу τ, після чого вона знову почне підвищуватися.

Таким чином, при використанні позиційного регулятора для керування об'єктом із запізнюванням виникають відхилення регульованого параметра від заданого значення Δθ⁺ і Δθ^– (див. рисунок 2.5). Для того, щоб оцінити величину цих відхилень будемо вважати, що після спрацьовування регулятора в моменти часу t₁, t₂, ... протягом часу запізнювання τ, регульований параметр буде змінюватися з постійною швидкістю. Тоді величину відхилення можна визначити помноживши цю швидкість на час запізнювання. А формулу для обчислення швидкості зміни параметра можна одержати з диференціального рівняння інерційної ланки. У результаті одержимо такі залежності для розрахунку величини відхилень:

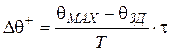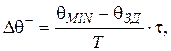(3.1)

де τ – час запізнювання об'єкта;

Т – постійна часу об'єкта;

θ_ЗД – задане значення температури;

θ_MAX, θ_MIN – сталі значення температури, що відповідають U_MAX, U_MIN (визначаються по статичній характеристиці об'єкта).

<== попередня сторінка	\|	наступна сторінка ==>
Висновки по роботі	\|	Опис експериментальної установки

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.