• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Інтегрування раціональних дробів

1. Розкладання многочленів на множники.

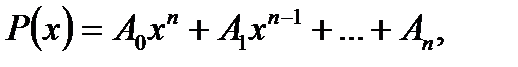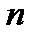Нагадуємо, що функція де – ціле додатне число, називається многочленом (поліномом) або цілою раціональною функцією від х. Число 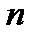називається степенем многочлена. При цьому 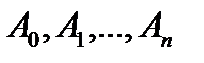– дійсні або комплексні сталі числа, 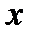– дійсна або комплексна змінна.

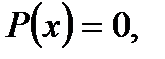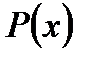Рівняння виду де – многочлен 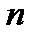- го степеня, називається алгебраїчним рівнянням 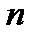-го степеня.

Основна теорема алгебри стверджує, що всяке алгебраїчне рівняння степеня 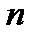>0 має хоча б один корінь, дійсний або комплексний.

Представимо 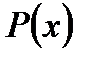у вигляді

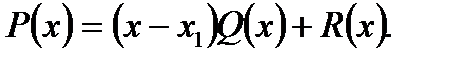
(тут 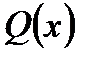многочлен, а 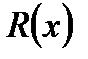– залишок від ділення 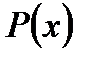на 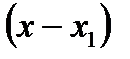). При 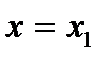виконується умова: 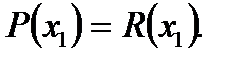Таким чином, залишок від ділення многочлена 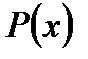на двочлен 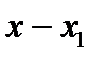при 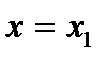дорівнює значенню цього многочлена 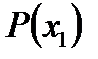(теорема Безу).

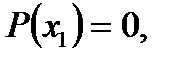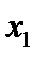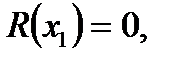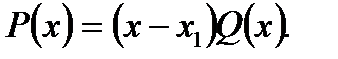Якщо тобто є коренем многочлена, то і Тут 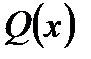– многочлен степеня 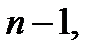старший коефіцієнт якого дорівнює 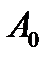. Якщо цей многочлен не є тотожно сталою, то до нього можна знову застосувати основну теорему алгебри. Якщо 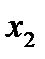– корінь рівняння 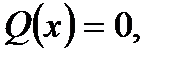то 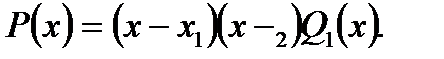Продовжуючи цей процес, одержуємо: 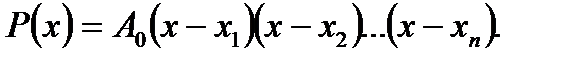Якщо кратність кореня 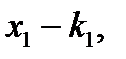кореня 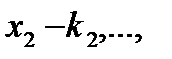кореня 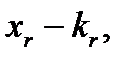то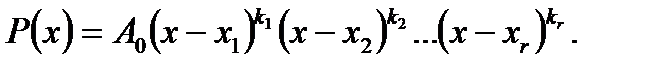

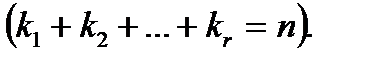
Отже, алгебраїчне рівняння 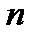- го степеня має 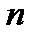коренів (якщо кожен корінь рахувати стільки разів, яка його кратність).

Якщо коефіцієнти многочлена 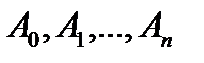– дійсні числа і комплексне число 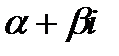є коренем многочлена 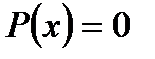, то спряжене йому, число 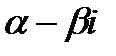також є коренем многочлена. Зауважимо, що зручно об’єднувати співмножники виду

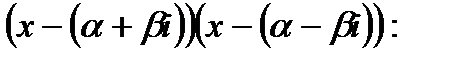
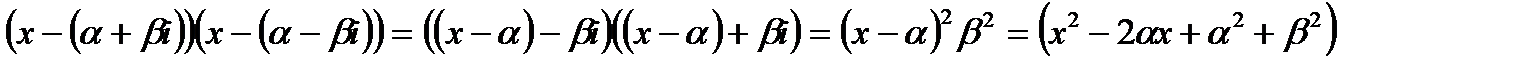. Таким чином, многочлен 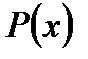можна розкласти на лінійні та квадратичні співмножники:

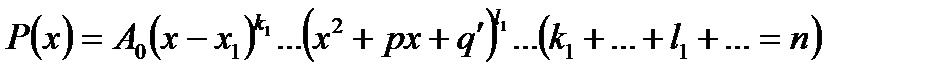
Якщо два многочлена рівні один одному при будь-яких значеннях 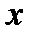, то рівня їх степені та рівні між собою коефіцієнти при однакових степенях: якщо

,

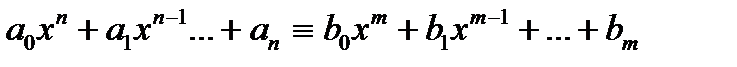то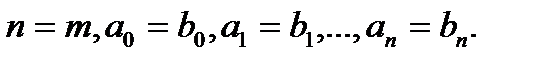

Зауваження. Для випадків, коли 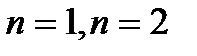рівняння 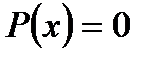розв’язуються за формулами, відомими з шкільного курсу математики. При 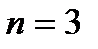та 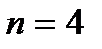також існують загальні формули розв’язування таких рівнянь – формули Кардано і Феррарі. Доведено, що при 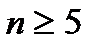не існує формул для розв’язування рівнянь 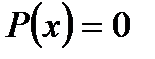в радикалах.

2. Розкладання раціональних дробів на найпростіші

Нехай многочлени 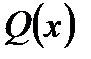та 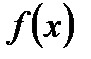не мають спільних коренів. Раціональним дробом називається відношення двох многочленів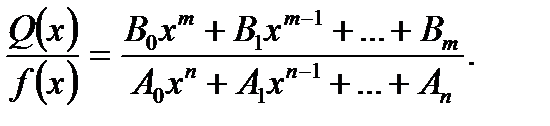

Якщо степінь чисельника менше степені знаменника, тобто 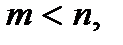то дріб називається правильним, якщо ж 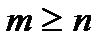– неправильним.

У випадку неправильного дробу чисельник ділять на знаменник та представляють даний дріб у вигляді суми многочлена та деякого правильного дробу: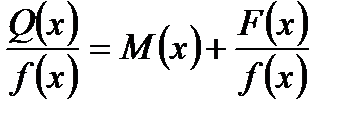

Після цього правильний нескоротний дріб 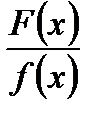розкладають на найпростіші раціональні дроби.

Правильні раціональні дроби виду

I.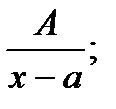

II. 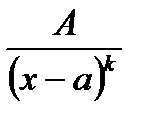( 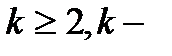ціле число);

III.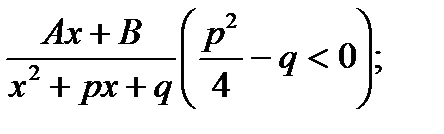

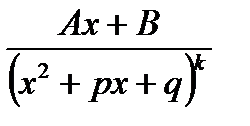
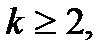
IV. 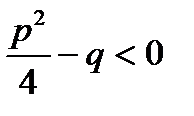називається найпростішими дробами І, ІІ, ІІІ, ІV типів.

Має місце

Теорема 1. Нехай 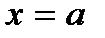корінь знаменника кратності 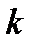, тобто 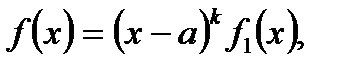де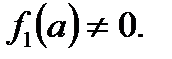

Тоді даний правильний нескоротний дріб 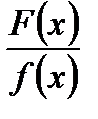можна представити у вигляді суми двох інших правильних дробів в такий спосіб:

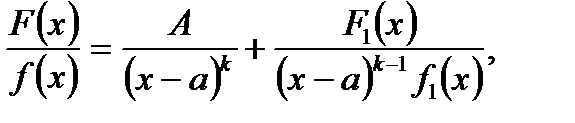
де 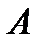– відмінне від нуля стале число, а 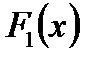– многочлен, степінь якого менше степеня знаменника .

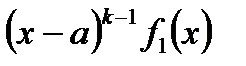Для доведення теореми 1 представимо дріб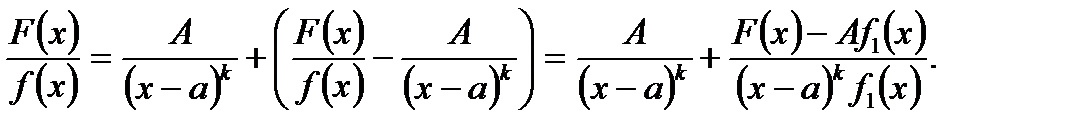

Підберемо А так, щоб різниця 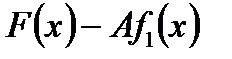ділилася на 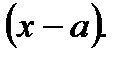Згідно з теоремою Безу, для цього необхідно і достатньо, щоб виконувалась умова

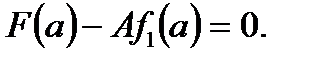
Звідси визначаємо: 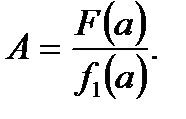Значить, саме при такому значенні А будемо мати: 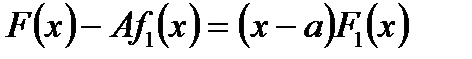. Це і доводить теорему 1.

Цю ж саму теорему 1 можна застосувати до виразу 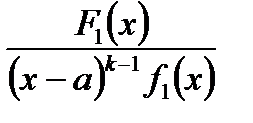. Оскільки 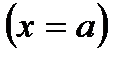– корінь кратності 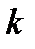, одержимо:

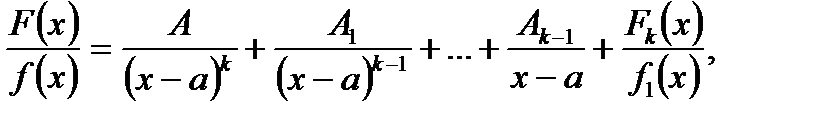де 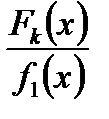– правильний нескоротний дріб. Має місце

Теорема 2. Якщо 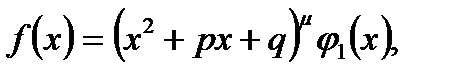причому 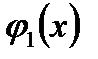не ділиться на 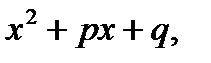то правильний раціональний дріб 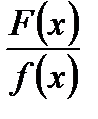можна представити у вигляді суми двох інших правильних дробів у такий спосіб:

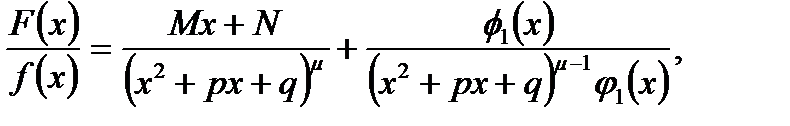
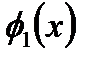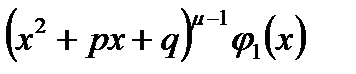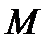де – многочлен, степінь якого менше степеня многочлена , а і 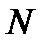– сталі.

Із теореми 1 і 2 випливає такий важливий для практичних застосувань

Висновок. Якщо 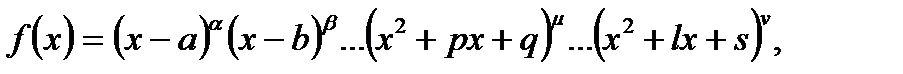то дріб 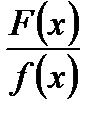можна представити у вигляді

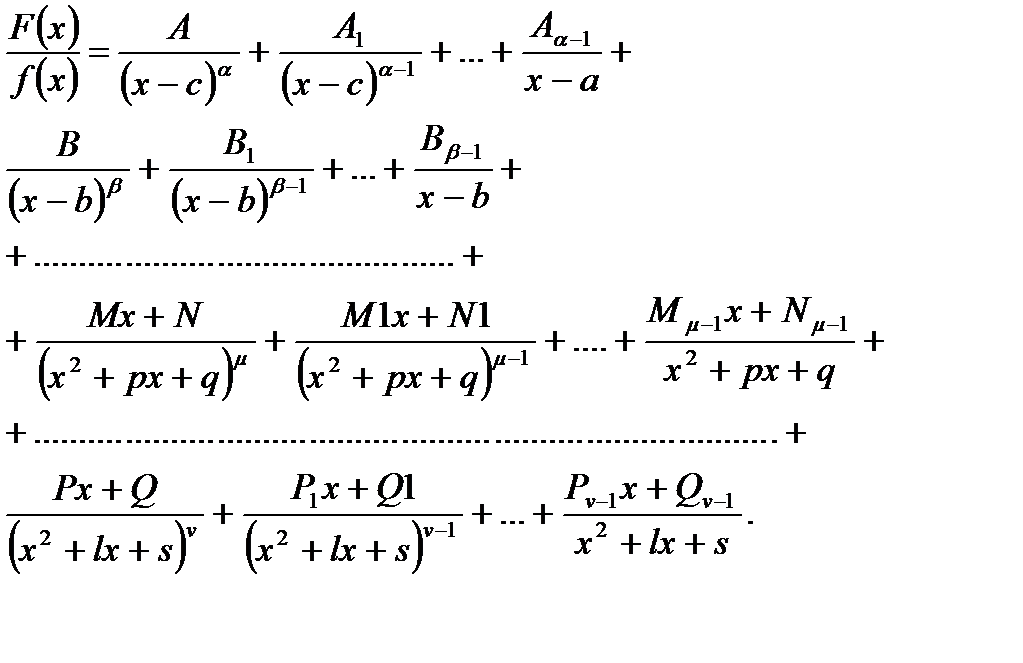
Для визначення невизначених коефіцієнтів вираз справа зводять до спільного знаменника, після чого (в чисельниках) прирівнюють коефіцієнти при однакових степенях хзліва і справа. Одержується система для визначення невідомих сталих.

Наприклад. Представити дріб 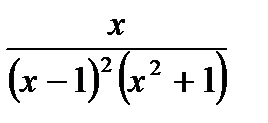у вигляді суми найпростіших дробів.

Розв’язування. Згідно з висновком з теорем 1 і 2, маємо:

.

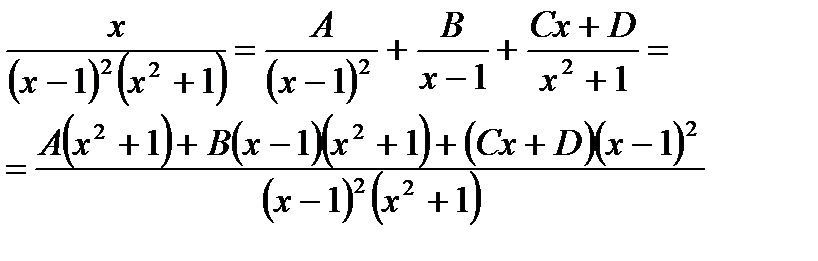Звідси одержуємо:

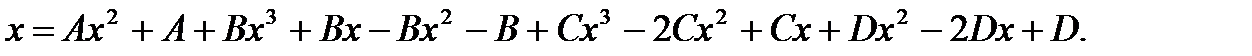
Прирівнюємо коефіцієнти при 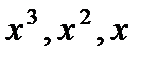та вільні члени зліва і справа одержуємо:

.

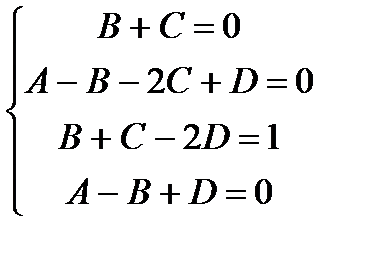Розв’язавши систему, маємо:

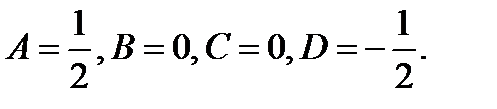
Таким чином,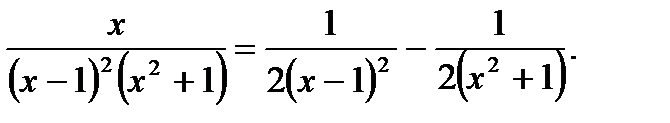

Зауваження. Для того, щоб одержати систему для визначення 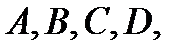можна скористатися методом коллокації, який полягає в тому, який полягає в тому, що рівняння

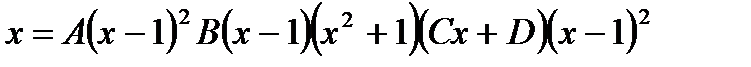
розписують при чотирьох (по кількості невідомих фіксованих) значеннях змінної х(наприклад, при ):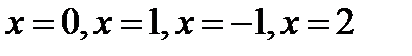

.

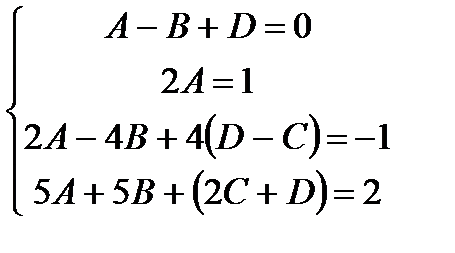Розвязуючм систему, одержуємо такий самий розв'язок, як і раніше.

Переглядів: 723