• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Нормальний закон розподілу

Нормальним називається розподіл ймовірностей неперервної випадкової величини, який описується щільністю

.

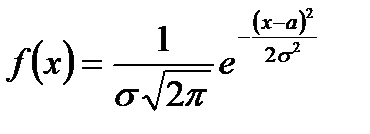Ляпунов довів, що коли випадкова величина 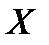є сумою дуже великого числа взаємно незалежних випадкових величин, вплив яких на всю суму надзвичайно малий, то 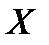має розподіл, близький до нормального.

Зупинимося детально на цьому законі розподілу.

Виявляється, що 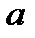– це математичне сподівання, а – середнє квадратичне відхилення нормального розподілу.

Зауважимо, що нормальний розподіл з довільними параметрами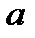

і 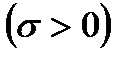називається загальним. Нормованим називають нормальний розподіл з параметрами 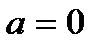і 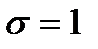. Якщо 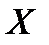– нормальна величина з параметрами 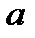і , то 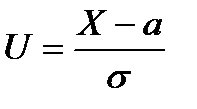– нормована нормальна величина, оскільки

,

.

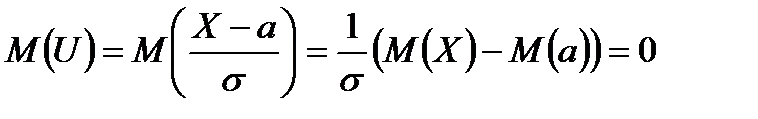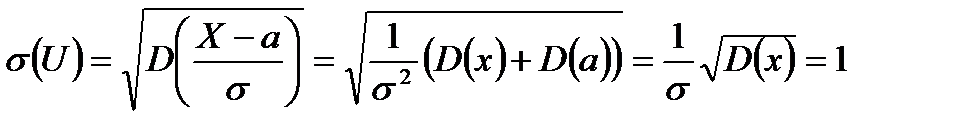Щільність нормального нормованого розподілу – це протабульована функція 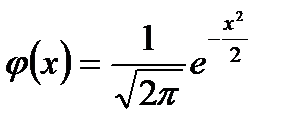, а інтегральна функція нормованого нормального розподілу – це функція 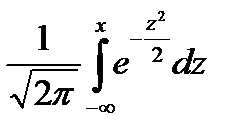. Таким чином, ймовірність попадання нормованої нормальної величини 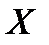в інтервал 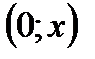можна обчислити, користуючись функцією Лапласа:

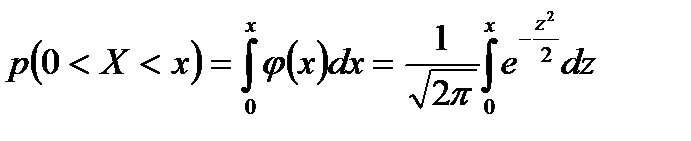(тобто ).

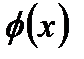Графік щільності загального нормального рівняння розподілу називається нормальною кривою (кривою Гаусса): .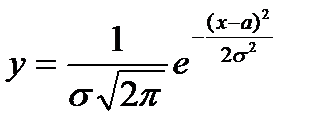

Областю визначення цієї функції є вся числова вісь: 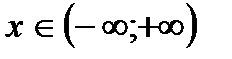. При цьому , 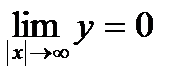. За допомогою першої похідної 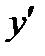неважко показати, що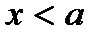 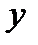монотонно зростає, а при 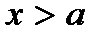– спадає; . Графік кривої Гаусса симетричний відносно осі 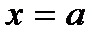. За допомогою похідної другого порядку визначаємо, що при 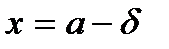та 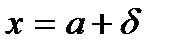крива має точки прегину, які відокремлюють проміжки увігнутості графіка 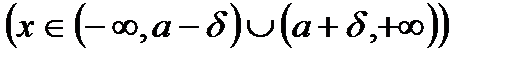від інтервалу його вигнутості вгору . Студентам рекомендується побудувати цей графік самостійно, використовуючи результати проведеного дослідження.

Зауважимо, що при зміні величина 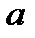форма нормальної кривої не змінюється; крива зсувається вздовж осі 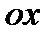вправо, якщо 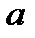зростає, та вліво, якщо 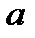спадає.

При зміні параметра площа, обмежена віссю 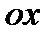і нормальною кривою, залишається незмінною. Але при зростанні максимальна ордината кривої спадає, а сама крива стає більш пологою, “ближчою” до осі 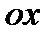. При зменшенні нормальна крива стає “гострішою”, розтягується в додатному напрямку осі .

Знайдемо ймовірність попадання в заданий інтервал нормально розподіленої випадкової величини:

.

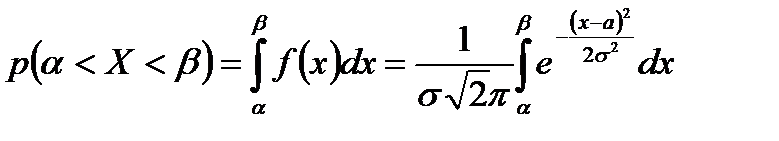Виконаємо заміну змінних 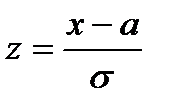; одержуємо:

,

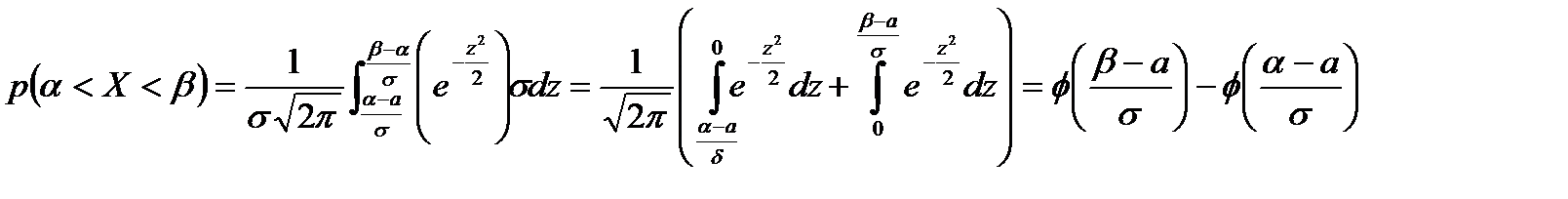де 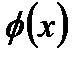– функція Лапласа. Отже, .

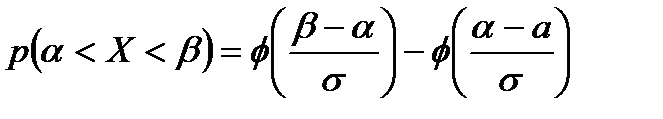За допомогою останньої рівності можна одержати формулу для обчислення ймовірності заданого відхилення 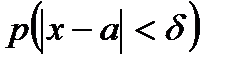. Дійсно,

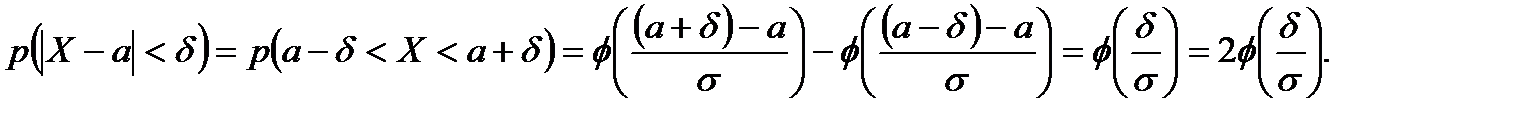Таким чином,

.

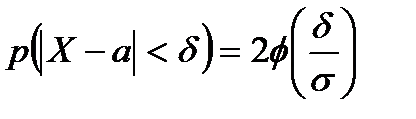З цієї формули випливає, що чим менше , тим більше 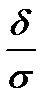і, значить, тим більша ймовірність .

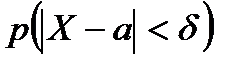Нехай 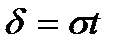. У цьому випадку маємо:

.

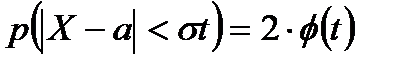При 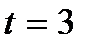, зокрема, одержуємо:

.

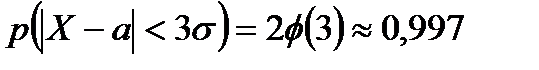Це – число, яке дуже мало відрізняється від одиниці. Таким чином, якщо випадкова величина розподілена нормально, то абсолютна величина її відхилення від математичного сподівання не перевищує потроєного середнього квадратичного відхилення.Це – правило трьох сигм.

Аналогічно доводиться правило двох сигм:

Якщо випадкова величина розподілена нормально, то абсолютна величина її відхилення від математичного сподівання з ймовірністю 0,954 не перевищує подвоєного середнього квадратичного відхилення:

.

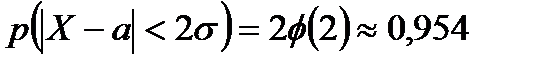Нормальному закону розподілу підпорядковуються будь-які розміри людського тіла (зріст, повнота і т.п.). Щоб задовольнити населення одягом, взуттям підходящих розмірів, потрібно знати, в якому асортименті слід випускати одяг і взуття тих чи інших розмірів.

Наприклад. Фабрика випускає 1000 штук чоловічих пальт в день для деякого регіону, де середній обхват грудей чоловічого населення дорівнює 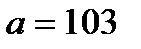см, причому 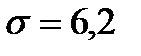см. Скільки виробів 48-го розміру повинна випускати фабрика в день, якщо цьому розміру відповідає інтервал обхвату грудей від 94 до 98 см?

Маємо:

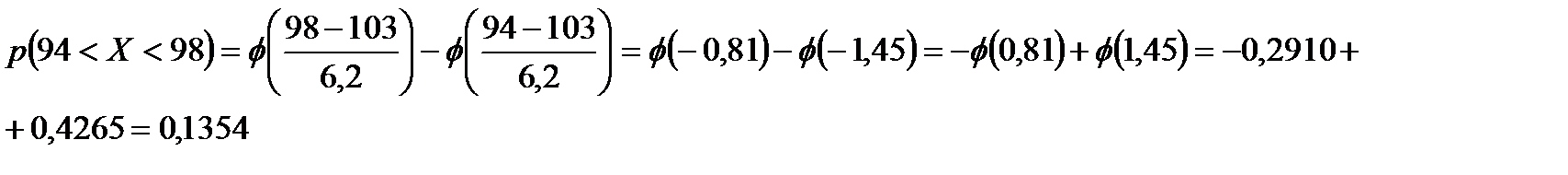(або 13,54%).

Це означає, що фабрика повинна випускати 135 пальт 48-го розміру.

Переглядів: 7630