
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
З метою глибокого засвоєння навчального матеріалу при самостійному вивченні теми студенту варто особливу увагу зосередити на таких аспектах.
1. Основні задачі теорії кореляції.
2. Побудова прямої лінії регресії.
3. Нелінійна кореляція.
1. Нехай задано дві випадкові величини – X і Y. Можливі такі ситуації.
1) X та Y – незалежні величини: зміна Х не впливає на розподіл Y.
2) X та Y пов’язані функціональною залежністю.
3) Між X та Y існує статистична (стохастична) залежність: одному й тому ж значенню величини X відповідає статистична сукупність значень величини Y. Якщо, зокрема, при зміні однієї величини (X) змінюється середнє значення другої ( 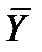 ), то статистична залежність називається кореляційною. Таким чином, кореляційна залежність – це функціональна залежність між значеннями величини X та умовними середніми значеннями випадкової величини Y.
), то статистична залежність називається кореляційною. Таким чином, кореляційна залежність – це функціональна залежність між значеннями величини X та умовними середніми значеннями випадкової величини Y.
Кореляція називається неповною, коли одній величині (наприклад, X) надаються певні фіксовані значення х1, х2,…,хк і для кожного з них шляхом експерименту знаходять сукупність значень величини Y. Кореляція називається повною, коли кожен із відібраних елементів статистичної сукупності об’єктів досліджується відразу і по Х, і по Y.
а) питання про форму кореляційного зв’язку між Х і Y;
б) оцінка тісноти кореляційного зв’язку між Х і Y.
Розв’язання задачі а) зводиться до підбору певного виду функціональної залежності, а задачі б) – визначення того, наскільки близька досліджувана залежність до вибраної функціональної.
Задача а) розв’язується за допомогою регресій. Емпірична лінія регресії – це ламана лінія, яка з’єднує точки з координатами Aі (xі, 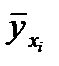 ) (тут
) (тут 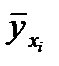 – умовна середня (і=1,2,…,n)). Теоретично лінією регресії Y по Х називається лінія, яка “згладжує” емпіричну лінію регресії. Рівняння цієї лінії дає наближений аналітичний вираз регресії.
– умовна середня (і=1,2,…,n)). Теоретично лінією регресії Y по Х називається лінія, яка “згладжує” емпіричну лінію регресії. Рівняння цієї лінії дає наближений аналітичний вираз регресії.
Кореляційна залежність між випадковими величинами Х та Y називається лінійною кореляцією, якщо теоретичні рівняння регресії Y по Х та Х по Y лінійні. В противному випадку кореляційна залежність називається нелінійною.
2. Параметри теоретичного рівняння прямої лінії регресії Y по Х знаходять у такий спосіб.
А) Якщо дано n точок ( 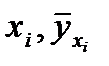 ) (і=1,2,…, n), шукають рівняння виду
) (і=1,2,…, n), шукають рівняння виду 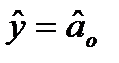
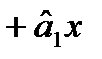 . Згідно з методом найменших квадратів, мінімізують суму квадратів відхилень виду
. Згідно з методом найменших квадратів, мінімізують суму квадратів відхилень виду 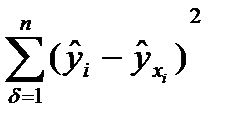 . Виходячи з цієї вимоги, одержують:
. Виходячи з цієї вимоги, одержують:
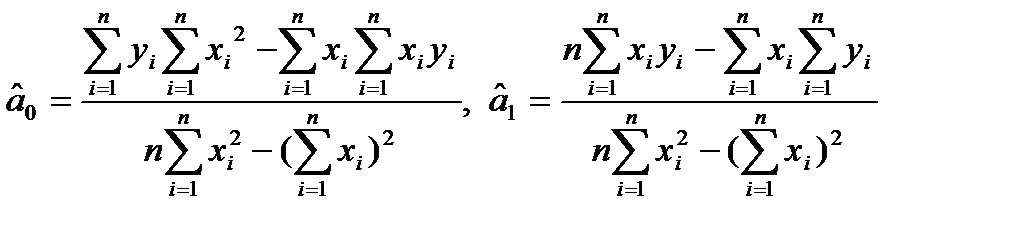 .
.
Аналогічно можна знайти рівняння прямої лінії регресії Х по Y: 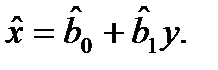 Зауважимо, що коефіцієнт
Зауважимо, що коефіцієнт 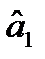 можна представити у вигляді
можна представити у вигляді 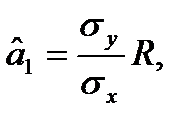 де σх та σу – вибіркові середні квадратичні відхилення, а R вибірковий коефіцієнт кореляції:
де σх та σу – вибіркові середні квадратичні відхилення, а R вибірковий коефіцієнт кореляції:
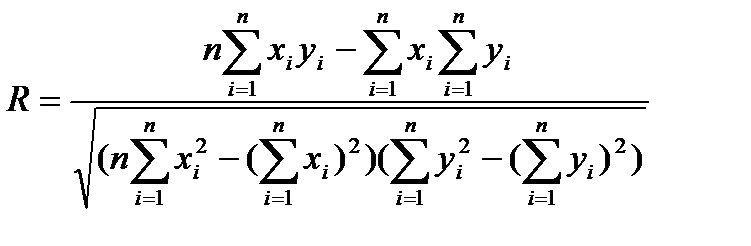
Цей коефіцієнт – статистична оцінка теоретичного коефіцієнта кореляції p, який визначається за формулою: 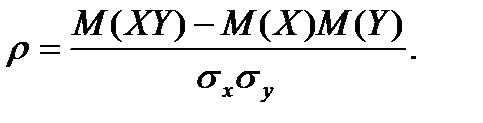
Б) Якщо дані спостереження над випадковими величинами Х і Y задані кореляційною таблицею розмір n х m з рівновіддаленими варіантами, то рівняння прямої лінії регресії Y по Х зручно шукати у формі 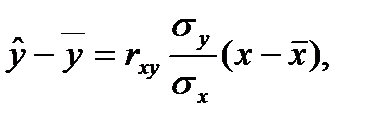 де
де 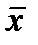 та
та 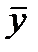 – вибіркові середні випадкових величин Х і Y відповідно, а rху – вибірковий коефіцієнт кореляції, представлений у вигляді
– вибіркові середні випадкових величин Х і Y відповідно, а rху – вибірковий коефіцієнт кореляції, представлений у вигляді 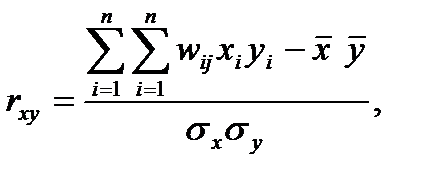 причому wij – емпірична ймовірність появи значення (хі,
причому wij – емпірична ймовірність появи значення (хі, 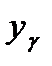 ) , n – кількість спостережених варіант випадкової величини X, m – кількість спостережених варіант випадкової величини Y.
) , n – кількість спостережених варіант випадкової величини X, m – кількість спостережених варіант випадкової величини Y.
Нехай результати спостережень задані кореляційною таблицею з рівновіддаленими варіантами, причому h1 – крок варіант випадкової величини Х, а h2 – крок варіант випадкової величини Y. Для полегшення розрахунків переходять до умовних варіант U і V, користуючись співвідношенням 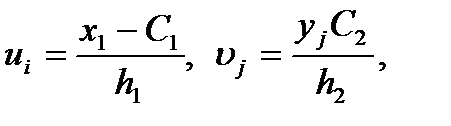 де C1 і C2 – “хибні нулі” варіант випадкових величин Х і Y. Вибірковий коефіцієнт кореляції
де C1 і C2 – “хибні нулі” варіант випадкових величин Х і Y. Вибірковий коефіцієнт кореляції 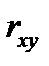 =
= 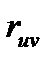 , де
, де 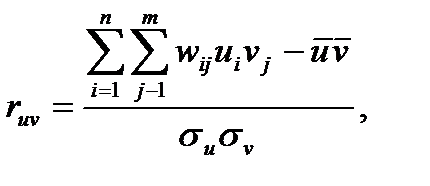 причому
причому
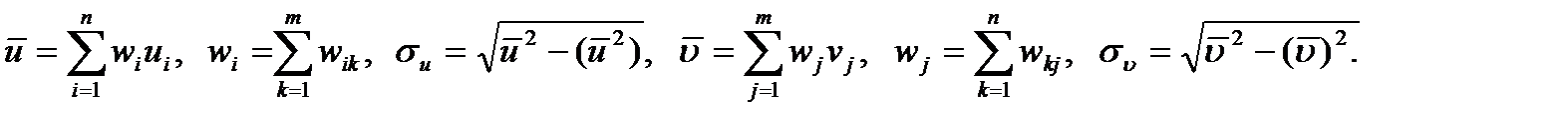
У рівняння прямої регресії виходять величини 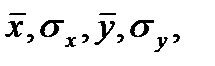 які обчислюють за допомогою формул
які обчислюють за допомогою формул 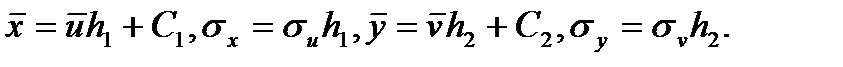
ПРИКЛАД. Знайти вибіркове рівняння прямої регресії Y по Х за даними кореляційної таблиці 1.
Таблиця 1
| Х | Y | nx | ||||
| - - - | - - | - - | - - | - - - | ||
| ny |
Розв’язування.Перетворимо кореляційну таблицю 1, ввівши умовні варіанти 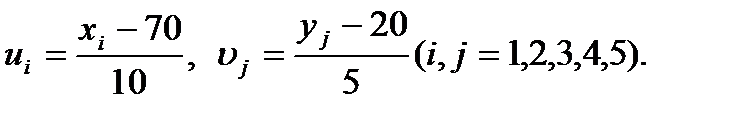 Замінимо частоти емпіричними ймовірностями. Отримаємо таблицю 2.
Замінимо частоти емпіричними ймовірностями. Отримаємо таблицю 2.
Таблиця 2
| U | V | wu | ||||
| -2 | -1 | |||||
| -2 -1 | 0,09 0,02 - - - | 0,09 0,10 0,03 - - | - 0,11 0,15 0,06 - | - - 0,12 0,10 0,01 | - - - 0,07 0,05 | 0,18 0,23 0,30 0,23 0,06 |
| wv | 0,11 | 0,22 | 0,32 | 0,23 | 0,12 |
Визначимо 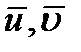 :
:
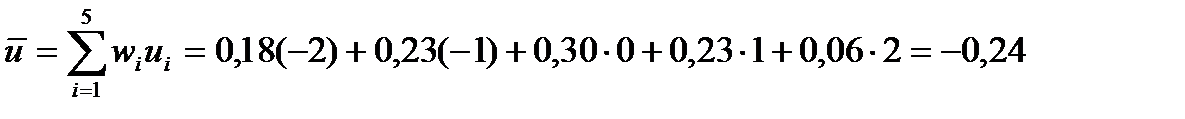 ;
;
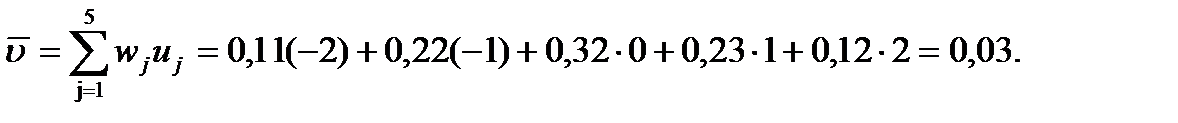
Знайдемо 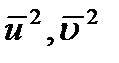 :
:
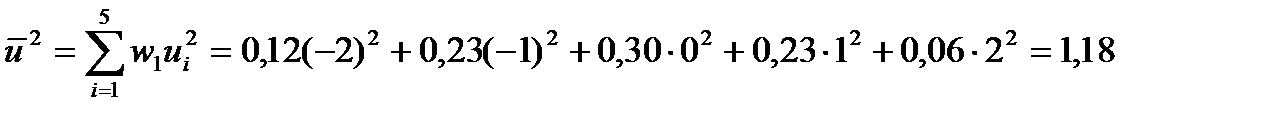 ;
;
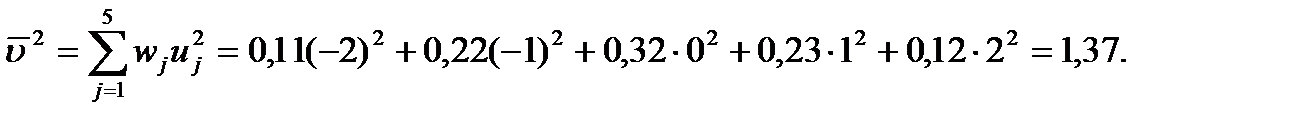
Обчислимо 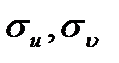 :
:
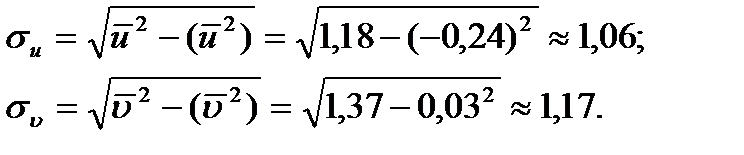
Далі знайдемо суму
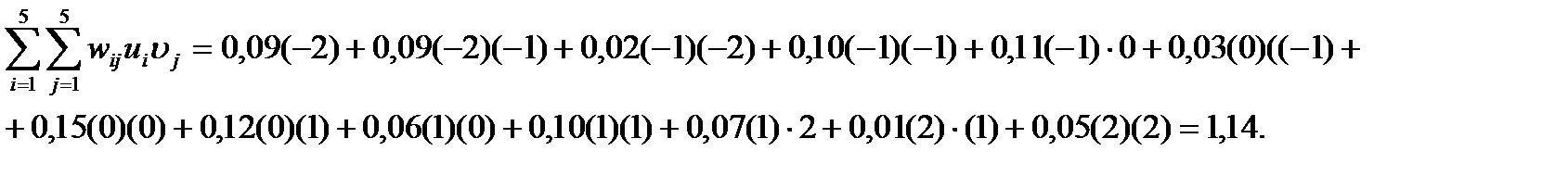
Знайдемо вибірковий коефіцієнт кореляції:
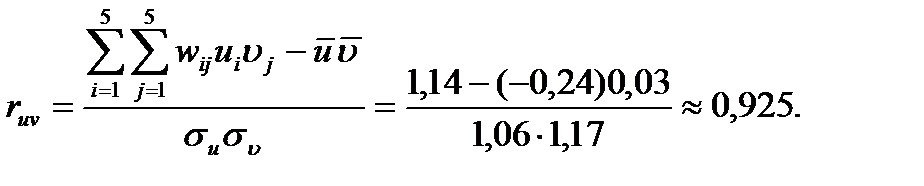
Звідси маємо: 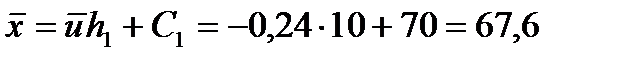 ,
, 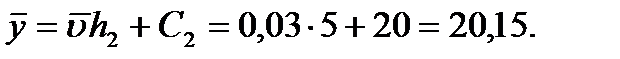 Обчислюємо середні квадратичні відхилення:
Обчислюємо середні квадратичні відхилення:
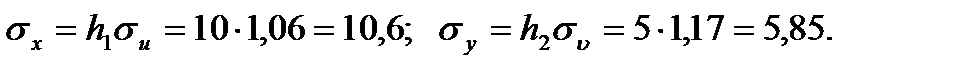
Таким чином, вибіркове рівняння регресії має вигляд 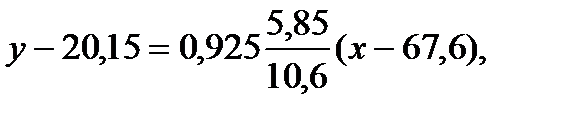 або
або 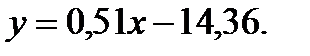
3. Припустимо, що точки кореляційного поля ґрупуються навколо деякої кривої лінії. У цьому випадку графік емпіричної лінії регресії співставляють з графіками відомих функцій. Невідомі параметри рівнянь регресії шукають методом найменших квадратів, провівши попередньо лінеаризацію (“випрямлення”) кривих. Так, наприклад, щоб піібрати параметри a і a1 степеневої залежності 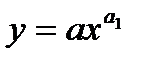 , лінеаризуємо це рівняння за допомогою логарифмування:
, лінеаризуємо це рівняння за допомогою логарифмування:
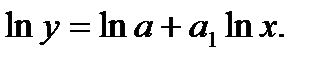
Якщо позначити 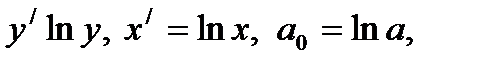 то останнє рівняння набуває виду
то останнє рівняння набуває виду
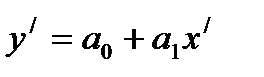
Параметри 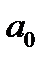 і
і 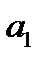 можна визначити методом найменших квадратів.
можна визначити методом найменших квадратів.
Оцінка точності апроксимації криволінійною залежністю проводиться за допомогою кореляційного відношення 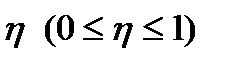 :
:
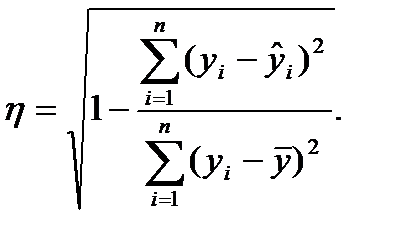
Якщо при цьому 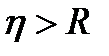 , то крива точніше апроксимує залежність, ніж пряма. При
, то крива точніше апроксимує залежність, ніж пряма. При 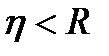 лінійна кореляція буде точнішою. Зауважимо, що для прямої лінії
лінійна кореляція буде точнішою. Зауважимо, що для прямої лінії 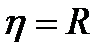 .
.
Важливе значення у прогнозуванні має логістична залежність
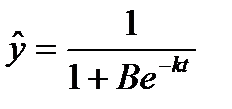 ,
,
причому B, k – сталі числа.
Якщо відомі результати n спостережень (ti, yi) (i=1,2,…,n), то ця залежність будується, як кореляційна. Заміною змінних
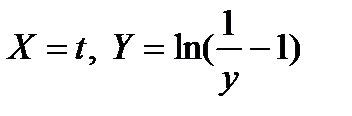
Вона лінеаризується у залежність 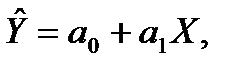 де
де 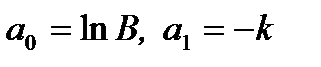 .
.
З використанням методу найменших квадратів для середніх значень параметрів В і k отримуємо формули:
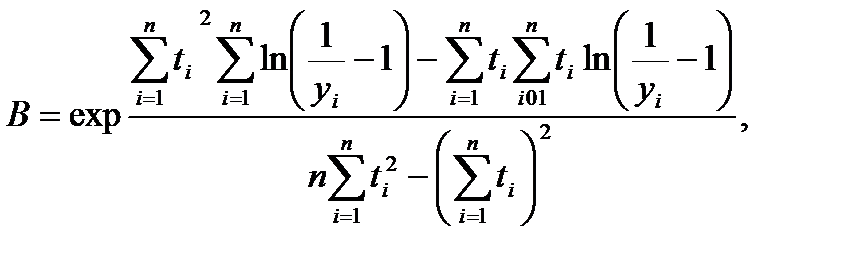
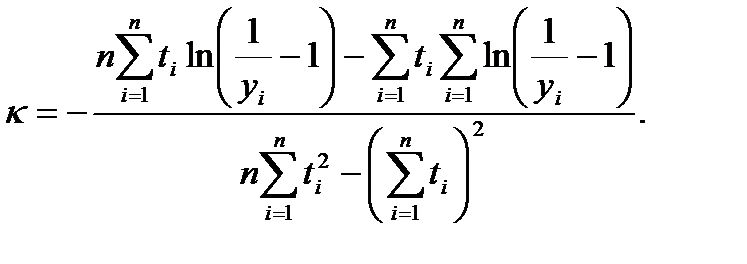
ПРИКЛАД. За щоденними даними першої декади червня рівня забезпеченості y населення послугою туристичного агентства (таблиця 1) встановити логістичну залежність.
Таблиця 1
| t (дні) | ||||||||||
| y | 0,195 | 0,200 | 0,205 | 0,210 | 0,220 | 0,230 | 0,240 | 0,255 | 0,270 | 0,285 |
Розв’язування. Обчислимо такі суми:
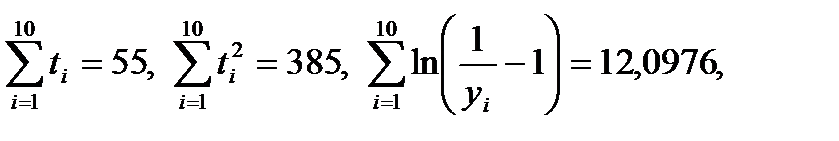
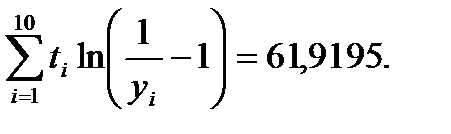
З використанням одержаних сум знаходимо: 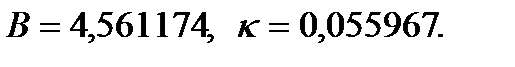
Відповідь: логістична залежність має вигляд 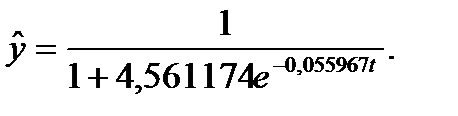
| <== попередня сторінка | | | наступна сторінка ==> |
| Семінарське заняття 27 | | | Поистине, Бог не меняет того, что |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |