
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Вступ до аналізу
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ОДЕСЬКИЙ НАЦІОНАЛЬНИЙ ЕКОНОМІЧНИЙ УНІВЕРСИТЕТ
Вища математика
Конспект лекцій
Для студентів 1 курсу денної форми навчання
Спеціальностей
«Товарознавство і торговельне підприємництво» та «Туризм»
Частина третя
| Затверджено на засіданні кафедри математичних методів аналізу економіки | |
| Протокол № від | |
Одеса ОНЕУ 2013
Вища математика. Конспект лекцій для студентів І курсу денної форми навчання спеціальностей «Товарознавство і торговельне підприємництво» та «Туризм». Частина третя(Уклад. О. Л. Суворовський, С. О. Пешкова - Одеса: ОНЕУ, ротапринт, 2013 р. - 56 с.)
Укладачш: О. Л. Суворовський, канд. екон. наук, доцент
С. О. Пешкова, ст. викладач
Рецензенти: О. В. Проценко, канд. ф.-м. наук, доцент
(зовнішній рецензент)
С. С. Клименко, канд. ф.-м. наук, доцент
В. М. Мацкул, канд. ф.-м. наук, доцент
Коректор: А. О. Ковальова
Передмова
Дана робота є результатом викладання протягом декількох років курсу „Вища математика” студентам перших курсів Одеського державного економічного університету. Вона містить першу частину курсу математичного аналізу.
Розглядаються поняття числових послідовностей, функцій, похідних та екстремумів функцій.
Усі формули, доведення і перетворення, наведені в роботі, містяться на електронних носіях, що дозволяє використовувати мультимедійну техніку під час читання курсу лекцій.
Вступ до аналізу
Означення 3.1. Абсолютною величиною, або модулем числа, називається саме число, якщо воно невід’ємне, та протилежне число, якщо воно від’ємне:
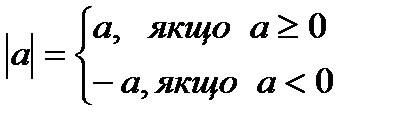
Властивості модуля
1. Модуль добутку дорівнює добутку модулів:
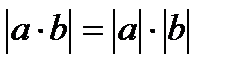 .
.
2. Модуль частки дорівнює частці модулів:
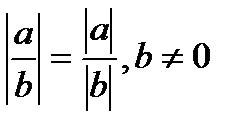 .
.
3. Модуль суми та різниці не більше суми модулів:
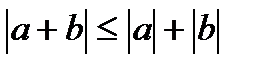 ,
, 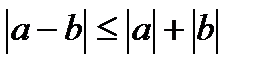 .
.
Геометричний зміст модуля числа: відстань від початку координат числової прямої до точки, яка відповідає числу 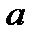 . У попередньому розділі ми визначили відстань між двома точками на прямій - модуль різниці координат:
. У попередньому розділі ми визначили відстань між двома точками на прямій - модуль різниці координат: 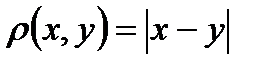 .
.
Означення 3.2. Числовим проміжком називається підмножина множини дійсних чисел 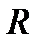 , яка на координатній прямій відображається у вигляді точки, інтервалу, напівінтервалу, відрізка, променя відкритого чи замкненого та їх об’єднань і перетинів.
, яка на координатній прямій відображається у вигляді точки, інтервалу, напівінтервалу, відрізка, променя відкритого чи замкненого та їх об’єднань і перетинів.
Приклади. Інтервал: 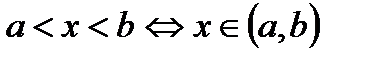 ;
;
напівінтервал: 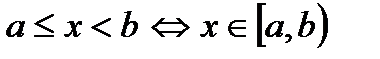 ;
;
відрізок: 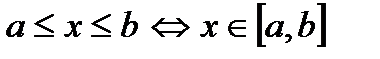 ;
;
відкритий промінь: 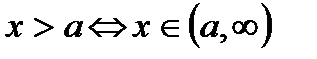 ;
;
замкнений промінь: 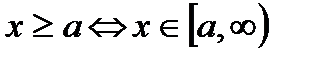 .
.
Означення 3.3. Епсілон-околом точки 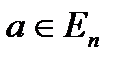 називається множина точок, відстань від яких до точки
називається множина точок, відстань від яких до точки 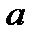 менша за додатне число
менша за додатне число 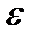 :
:
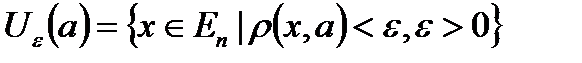
В одновимірному просторі 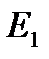 , або
, або 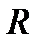 , відстань визначається модулем різниці координат, отже:
, відстань визначається модулем різниці координат, отже: 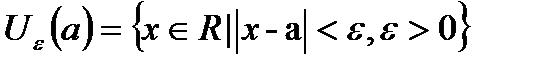 .
.
Означення 3.4. Функцією називається відображення множини 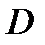 на множину
на множину 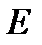 , при якому кожному елементу множини
, при якому кожному елементу множини 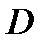 відповідає єдиний елемент множини
відповідає єдиний елемент множини 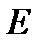 :
:
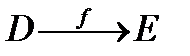 ,
,
де 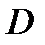 - область визначення,
- область визначення, 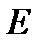 - множина значень функції
- множина значень функції 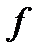 .
.
Нехай 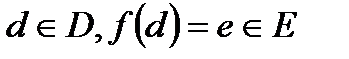 . Тоді
. Тоді 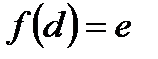 - образ
- образ 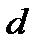 , а
, а 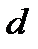 - прообраз
- прообраз 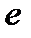 .
.
Зворотним до відображення 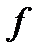 називається відображення образів на прообрази, воно позначається
називається відображення образів на прообрази, воно позначається 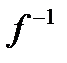 :
:
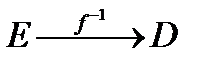 .
.
Зворотне зображення до функції не завжди є функцією.
Означення 3.5. Функція називається такою, що має обернену, якщо зворотне відображення до неї також є функцією.
Така пара функцій називається взаємооберненою, і кожна з них – взаємооднозначною.
Означення 3.6. Функція називається числовою, якщо область визначення та множина значень є підмножинами множини дійсних чисел:
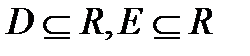 .
.
Числа з множини 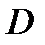 позначають змінною величиною
позначають змінною величиною 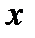 , вона називається незалежною змінною або аргументом, а числа із множини
, вона називається незалежною змінною або аргументом, а числа із множини 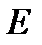 позначають змінною величиною
позначають змінною величиною 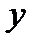 , вона називається залежною змінною або функцією.
, вона називається залежною змінною або функцією.
Існує три способи задання функцій:
- табличний;
- графічний;
- аналітичний.
У першому випадку в таблицю записують пари відповідних значень 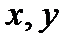 . Зрозуміло, що таким чином можна задати функцію, у якій множини
. Зрозуміло, що таким чином можна задати функцію, у якій множини 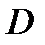 та
та 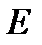 містять скінчену кількість чисел або ці множини є ліченими.
містять скінчену кількість чисел або ці множини є ліченими.
При графічному задані функція задається графіком.
Означення 3.7. Графіком функції 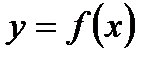 називається множина точок координатної площини, координати яких є
називається множина точок координатної площини, координати яких є 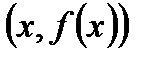 .
.
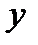
|
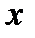
|
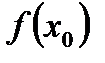
|
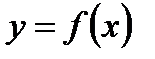
|
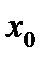
|
Абсциси точок – числа з області визначення 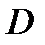 , а ординати – відповідні значення з
, а ординати – відповідні значення з 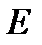 . Область визначення в такий спосіб заданої функції – ортогональна проекція графіка на вісь абсцис, а множина значень – ортогональна проекція на вісь ординат.
. Область визначення в такий спосіб заданої функції – ортогональна проекція графіка на вісь абсцис, а множина значень – ортогональна проекція на вісь ординат.
При аналітичному способі визначення функції задається аналітичний вираз відносно аргументу, за яким обчислюється відповідні значення функції:
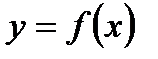 .
.
Область визначення в такому випадку є ОДЗ відповідного аналітичного виразу. Така область визначення називається природною.
| <== попередня сторінка | | | наступна сторінка ==> |
| | | Основні властивості функцій |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |