Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Задачі до розділу 4.1

Задача 4.1.1

В ящику 30 виробів: 20 стандартних і 10 підвищеної якості. Витягли підряд 4 вироба, причому кожний вироб повертали назад до ящика перед вилученням другого і вироби в ящику змішувалися. Яка ймовірність того, що серед вилучених 4 виробів будуть 2 стандартні?

Рішення

Ймовірність вилучення стандартного виробу 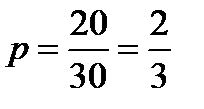можна вважати однаковою у всіх чотирьох випробуваннях. Тоді ймовірність протилежної події (вилучення виробу підвищеної якості) дорівнює 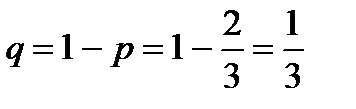. Використовуючи формулу Бернуллі (4.1), одержимо:

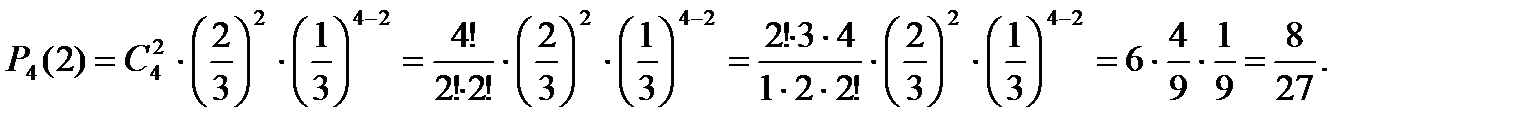
Задача 4.1.2

Ймовірність появи події А дорівнює 0,4. Яка ймовірність того, що при 10 випробуваннях подія А з’явиться не більше 3 раз?

Рішення.

З умови задачі: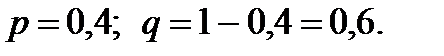

Ймовірність появи події А 0 раз: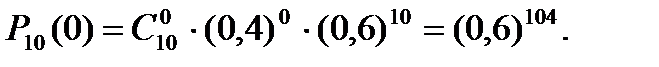

Ймовірність появи події А 1 раз: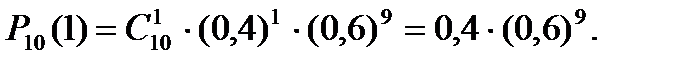

Ймовірність появи події А 2 рази: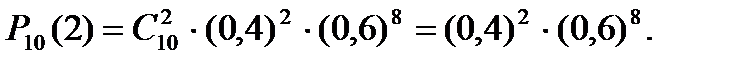

Ймовірність появи події А 3 рази: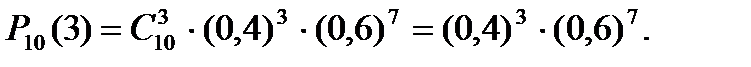

Ймовірність того, що подія А з’явиться не більше 3 раз, визначається із виразу

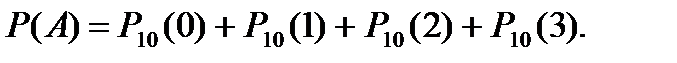
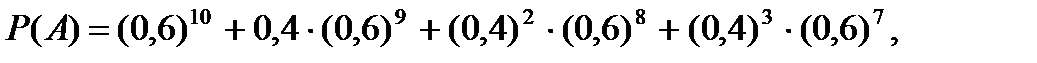
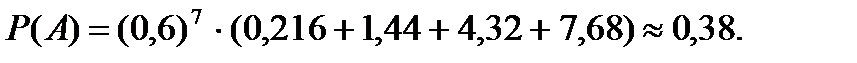
Задача 4.1.3

Обчислити ймовірність появи події А рівно 3 рази у 7 випробуваннях, якщо ймовірність появи події у кожному випробуванні однакова і дорівнює 0,6.

Задача 4.1.4

Ймовірність купівлі одиниці бракованого товару дорівнює 0,1. Знайти ймовірність того, що з 7 куплених одиниць товару 5 буде без браку.

Задача 4.1.5

Визначити ймовірність того, що у родині, яка має шестеро дітей, буде 2 хлопчика і чотири дівчинки. Ймовірність народження хлопчика вважати рівною 0,51.

Задача 4.1.6

Два рівносильних гравця грають у шахи. Що є більш вірогідним:

а) виграти одну партію з двох або дві партії з чотирьох?

б) виграти не менше двох партій з чотирьох або не менше трьох партій з п’яти? Вважати, що нічийний результат не береться до уваги.

Задача 4.1.7

Пристрій складається з трьох основних незалежно працюючих елементів. Пристрій не працює, якщо відмовиться працювати хоча б один його елемент. Ймовірність відмови кожного елемента за певний час дорівнює 0,2. Знайти ймовірність безвідмовної роботи пристрою за певний час, якщо:

а) працюють тільки основні елементи;

б) підключено один резервний елемент;

в) підключено два резервних елемента.

Припускається, що резервні елементи працюють у тому ж режимі, що і основні. Ймовірність відмови кожного резервного елемента дорівнює 0,2 і пристрій не працює, коли працює менше трьох елементів.

Розділ 4.2. Локальна теорема Лапласа

Легко бачити, що в разі великих значень п користуватися формулою Бернуллі достатньо важко. Наприклад, якщо 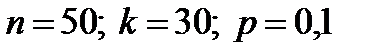, тоді за формулою (4.1) і необхідно зробити обчислення 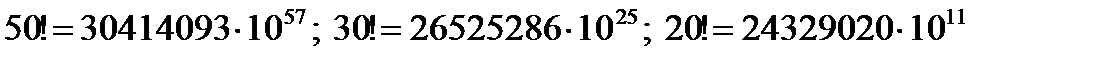,які є досить обтяжливими. Тому існує формула, яка дозволяє наближено знайти ймовірність того, що при п випробуваннях подія А з’явиться рівно 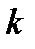раз, якщо число іспитів достатньо велике.

Цю асимптотичну формулу для р=0,5 було знайдено у 1730 році Муавром, а у 1783 році Лаплас узагальнив її для довільної р, відмінної від 0 та 1, тому іноді її називають теоремою Муавра-Лапласа.

Теорема: Якщо ймовірність р появи події А в кожному випробуванні постійна і відмінна від нуля і одиниці, тоді ймовірність 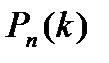того, що подія А з’явиться в п випробуваннях рівно k раз, наближено дорівнює (тим точніше, чим більше п) значенню функції

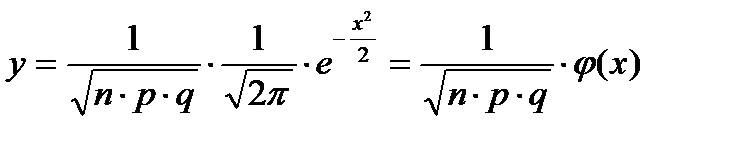, (4.2)

при .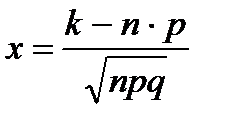

Існують таблиці, в яких розміщені значення функції 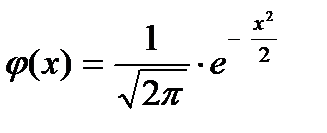, які відповідають додатнім значенням аргументу 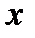. Для від’ємних значень аргументу користуються тією ж таблицею, оскільки функція 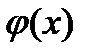є парною, тобто .

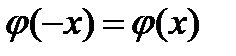Приклад:

Знайти ймовірність того, що подія А з’явиться рівно 80 раз у 400 випробуваннях, якщо ймовірність появи цієї події у кожному випробуванні дорівнює 0,2.

<== попередня сторінка	\|	наступна сторінка ==>
Рішення	\|	Рішення

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.017 сек.