
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Розділ 7.1. Доцільність введення числової характеристики розсіювання випадкової величини
Досить часто зустрічаються такі випадки, коли випадкові величини мають однакові математичні сподівання, але різні можливі значення.
 Приклад:
Приклад:
Дискретні випадкові величини Х та У задано наступними законами розподілу
| Х | -0,01 | 0.01 |
| Р | 0,5 | 0,5 |
| У | -100 | |
| Р | 0,5 | 0,5 |
Знайдемо математичне сподівання цих величин
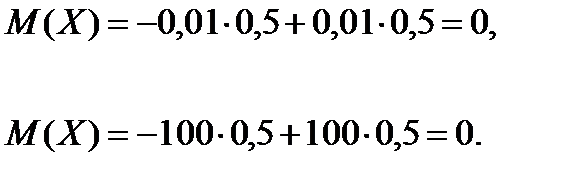
Як видно, математичне сподівання приймає однакові значення, а можливі значення різні, причому дискретна випадкова величина Х має можливі значення ближчі до математичного сподівання, ніж дискретна випадкова величина У. Таким чином, за величиною математичного сподівання не можна судити про можливі значення дискретної випадкової величини, про те, як ці можливі значення розсіяні навколо математичного сподівання. Іншими словами, математичне сподівання повністю не характеризує дискретну випадкову величину Х.
Тому на ряду з математичним сподіванням вводять і інші числові характеристики, що характеризують відхилення (розсіювання) випадкової величини від її середнього значення: дисперсію і середнє квадратичне відхилення.
Розділ 7.2. Дисперсія дискретної випадкової величини та її властивості. Середнє квадратичне відхилення
Перед тим, як перейти до означення і властивостей дисперсії, введемо поняття відхилення випадкової величини від її математичного сподівання.
Нехай Х – випадкова величина і 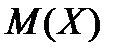 - її математичне сподівання. Розглянемо як нову випадкову величину різницю
- її математичне сподівання. Розглянемо як нову випадкову величину різницю 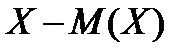 . Відхиленням називається різниця між випадковою величиною та її математичним сподіванням.
. Відхиленням називається різниця між випадковою величиною та її математичним сподіванням.
 Теорема: Математичне сподівання відхилення випадкової величини від її математичного сподівання дорівнює нулю, тобто
Теорема: Математичне сподівання відхилення випадкової величини від її математичного сподівання дорівнює нулю, тобто
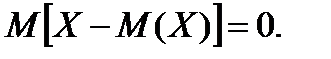
Доведення
Використовуючи спочатку властивість 4 математичного сподівання, а потім властивості 1 і 2 одержуємо
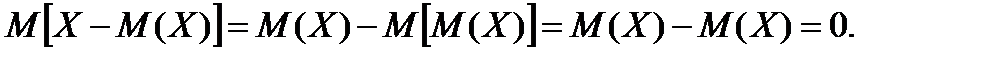
Тому це відхилення 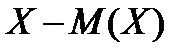 у подальшому не розглядається як характеристика розсіювання випадкової величини. У цьому випадку прийнято вивчати квадрат відхилення
у подальшому не розглядається як характеристика розсіювання випадкової величини. У цьому випадку прийнято вивчати квадрат відхилення 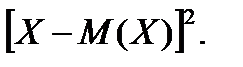
 Означення: Дисперсією або розсіюванням дискретної випадкової величини називається математичне сподівання квадрата відхилення випадкової величини від її математичного сподівання, позначається
Означення: Дисперсією або розсіюванням дискретної випадкової величини називається математичне сподівання квадрата відхилення випадкової величини від її математичного сподівання, позначається
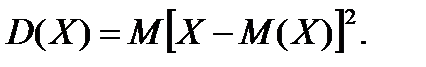 (7.1)
(7.1)
Якщо врахувати означення математичного сподівання (див. формулу 6.2), то вираз для дисперсії 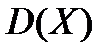 із формули (7.1) можна записати у розгорнутому вигляді так
із формули (7.1) можна записати у розгорнутому вигляді так
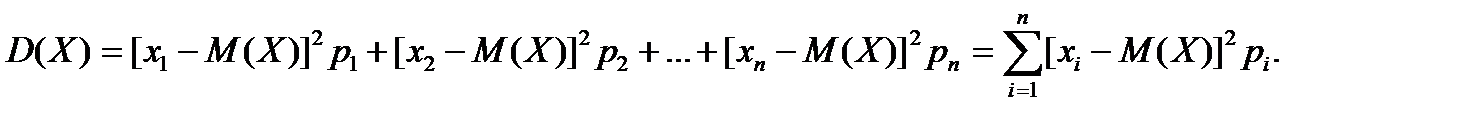 (7.2)
(7.2)
Формула (7.1) незручна при обчисленнях, тому перетворимо її і подамо у більш зручному вигляді. Для цього застосуємо теорему.
 Теорема: Дисперсія дорівнює різниці між математичним сподіванням квадрата випадкової величини та квадратом її математичного сподівання
Теорема: Дисперсія дорівнює різниці між математичним сподіванням квадрата випадкової величини та квадратом її математичного сподівання
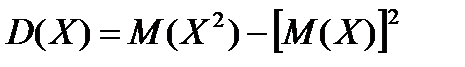 (7.3)
(7.3)
Доведення
Із означення дисперсії випливає
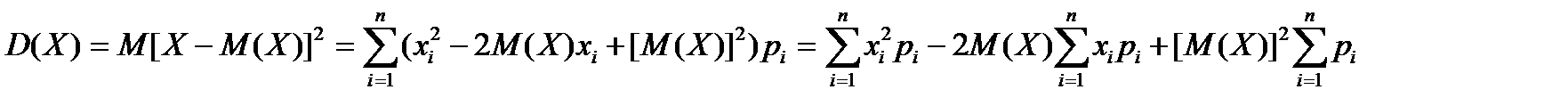 .
.
Оскільки 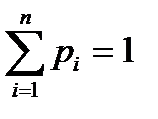 і
і 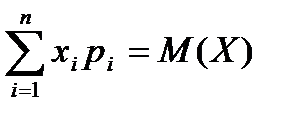 , то ввівши позначення
, то ввівши позначення
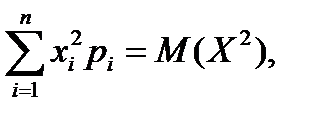 (7.4)
(7.4)
отримаємо далі
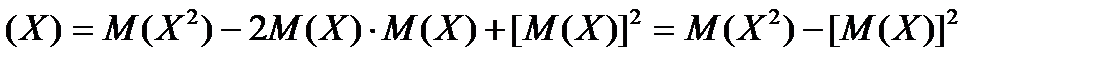
Таким чином, остаточно отримуємо
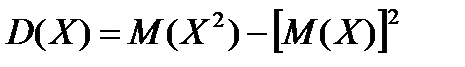 ,
,
де 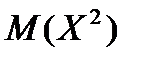 – математичне сподівання квадрата випадкової величини, знаходиться за формулою (7.4), а
– математичне сподівання квадрата випадкової величини, знаходиться за формулою (7.4), а 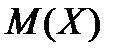 – математичне сподівання за формулою (6.2) заняття 6.
– математичне сподівання за формулою (6.2) заняття 6.
 Приклад:
Приклад:
1. Знайти дисперсію випадкової величини, заданої законом розподілу
| Х | |||
| Р | 0,2 | 0,5 | 0,3 |
Рішення
Знайдемо спочатку математичне сподівання випадкової величини Х
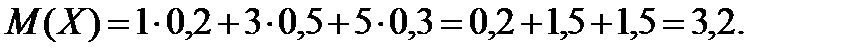
Тепер знайдемо математичне сподівання квадрата випадкової величини, для цього складемо розподіл
| Х2 | |||
| Р | 0,2 | 0,5 | 0,3 |
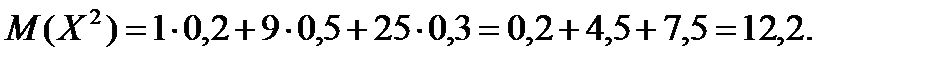
За формулою (7.3) маємо
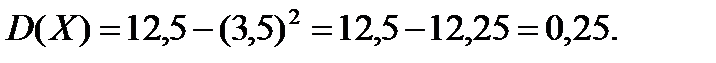
 Розглянемо основні властивості дисперсії.
Розглянемо основні властивості дисперсії.
Властивість 1. Дисперсія сталої величини дорівнює нулю
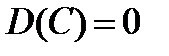 .
.
Доведення
За формулою (7.3) маємо
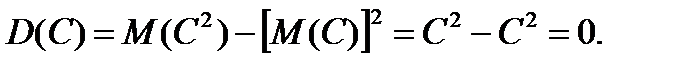
Властивість 2. Сталий множник можна виносити за знак дисперсії, піднісши його до квадрата, тобто
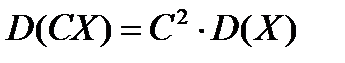 .
.
Доведення
За означенням дисперсії маємо
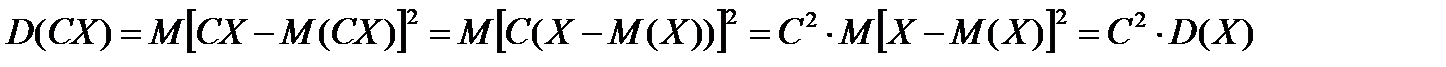 .
.
Властивість 3. Дисперсія суми двох випадкових величин дорівнює сумі дисперсії цих величин, тобто
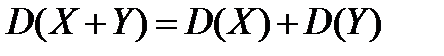 .
.
Доведення
За формулою (7.3) маємо
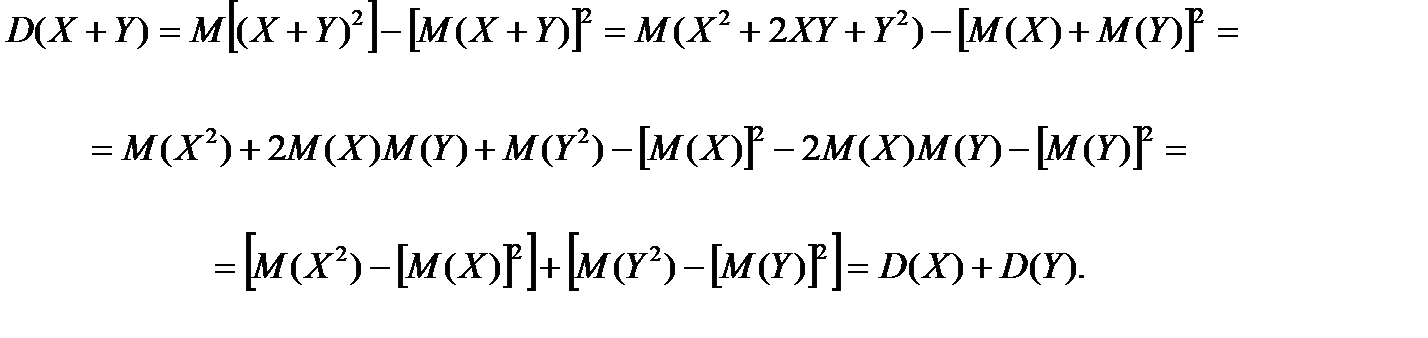
Властивість 4. Дисперсія суми випадкової величини і сталої дорівнює дисперсії випадкової величини
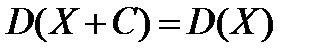 .
.
Доведення
Використаємо властивості 1 і 3 дисперсії
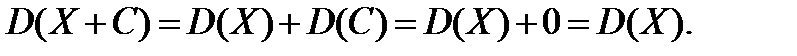
Властивість 5. Дисперсія різниці двох випадкових величин дорівнює сумі дисперсій цих випадкових величин
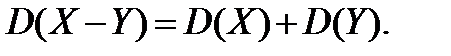
Доведення
Відповідно до властивостей 2 і 3 маємо:
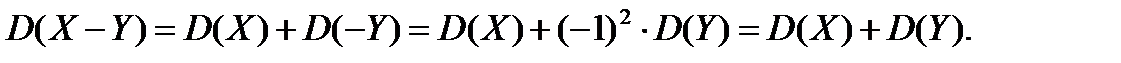
 Означення: Середнім квадратичним відхиленням випадкової величини називається корінь квадратний із дисперсії і позначається
Означення: Середнім квадратичним відхиленням випадкової величини називається корінь квадратний із дисперсії і позначається
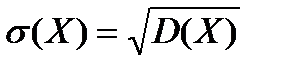 . (7.5)
. (7.5)
| <== попередня сторінка | | | наступна сторінка ==> |
| Задачі до розділу 6.3 | | | Задачі до розділу 7.2 |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |