• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Асиметрія і ексцес

Означення: Коефіцієнтом асиметрії А називається відношення центрального моменту третього порядку до куба середнього квадратичного відхилення

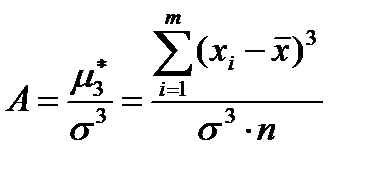. (13.6)

Якщо у варіаційному ряді більше варіант таких, що 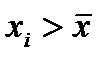, тоді коефіцієнт асиметрії додатній, та має місце правостороння асиметрія. Якщо ж 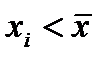, тоді має місце лівостороння асиметрія.

Означення: Ексцесом або коефіцієнтом крутості Е називається зменшене на три одиниці відношення центрального моменту четвертого порядку до четвертої степені середнього квадратичного відхилення

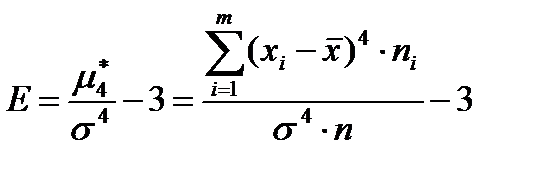. (13.7)

Якщо , тоді криві менш круті і називаються плоско вершинними, якщо 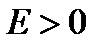- більш круті, мають більш гостру вершину і називаються гостро вершинними.

Приклад:

Для попереднього прикладу про розподіл 49 промислових підприємств за швидкістю обігових коштів, знайти асиметрію і ексцес.

Рішення

Для знаходження асиметрії і ексцесу складемо розрахункову таблицю

№п/п	-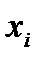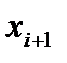
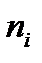
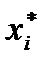
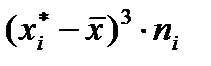
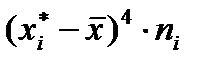
	20 – 30				2699,66	-49592,75	911018,82
	30 – 40				770,63	-6450,17	53987,92
	40 – 50				42,51	69,29	112,94
	50 – 60				1217,31	14157,32	164649,63
	60 - 70				2339,28	50598,63	1094448,37
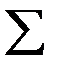
					7069,39	8782,32	2224217,68

Обсяг генеральної сукупності 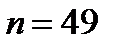, тоді за формулою (12.2) заняття 12 знайдемо середню арифметичну

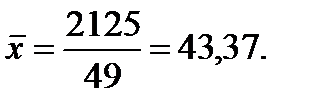
Тоді за формулою (12.4) і (12.5) заняття 12 знайдемо дисперсію і середнє квадратичне відхилення

.

За формулою (13.6) знайдемо асиметрію

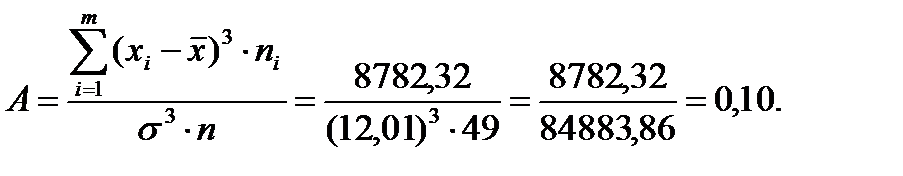
За формулою (13.7) знайдемо ексцес

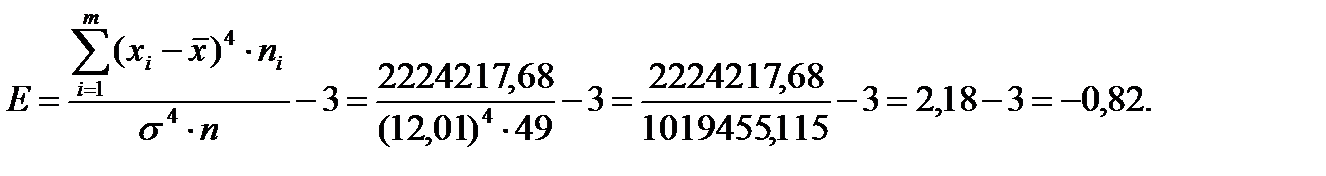
Розділ 13.5. Завдання до заняття 13

Теоретичні питання до заняття 13

1. Дати означення коефіцієнта варіації.

2. Що характеризує коефіцієнт варіації?

3. Дати означення медіани варіаційного ряду.

4. Як обчислюється медіана при дискретному розподілі, якщо обсяг виборки є непарним?

5. Як обчислюється медіана при дискретному розподілі, якщо обсяг виборки є парним?

6. Як обчислюється медіана при неперервному розподілі? Записати формулу та пояснити її складові.

7. Дати означення моди варіаційного ряду?

8. Як обчислюється мода при дискретному розподілі?

9. Як обчислюється мода при неперервному розподілі? Записати формулу та пояснити її складові.

10. Дати означення початкового моменту варіаційного ряду. Записати формулу та пояснити її складові.

11. Дати означення центрального моменту варіаційного ряду. Записати формулу та пояснити її складові.

12. Дати означення асиметрії. Записати формулу та пояснити її складові.

13. Що характеризує асиметрія?

14. Дати означення ексцесу. Записати формулу та пояснити її складові.

15. Що характеризує ексцес?

Переглядів: 6794