• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Теорема (ознака Абеля).

.

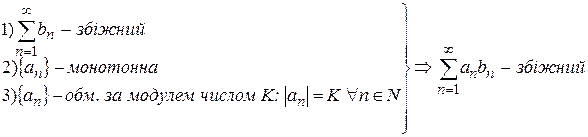Теорема (ознака Діріхле).

.

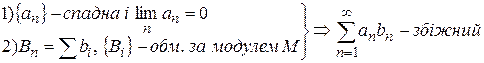Теорема (ознака Лейбніца).

.

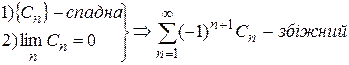Означення. 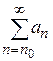– абсолютно збіжний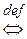 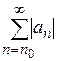– збіжний.

Означення. 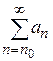– умовно збіжний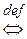

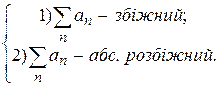
Властивості:

Теорема. 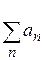– абсолютно збіжний 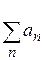– збіжний.

Теорема. Абсолютно збіжний ряд при переставленні своїх членів не змінює суму.

Теорема (Рімана). Якщо числовий ряд 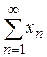збігається умовно, тоді

1) для будь-якого дійсного числа 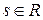знайдеться переставлення , для якого ;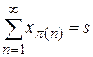

2) можна побудувати таке переставлення 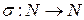, що .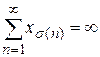

Теорема.

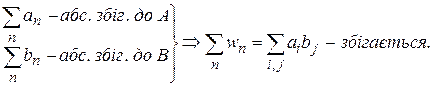
Причому .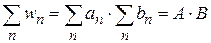

Теорема Мертенса. Якщо один із рядів 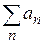чи 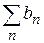збігається абсолютно, а інший хоча б умовно, тоді буде збігатися ряд спеціального виду:

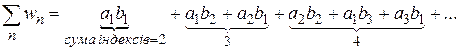– збігається до добутку значень сум цих рядів, тобто .

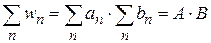Степеневі ряди. Теорема Абеля про область збіжності степеневого ряду. Формула Коші-Адамара для визначення радіуса збіжності. Рівномірна збіжність, диференціювання і інтегрування степеневих рядів.

Означення. Функціональний ряд вигляду:

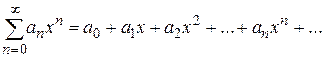називається степеневим рядом, а числа 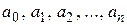– коефіцієнтами степеневого ряду.

Очевидно, що кожен степеневий ряд збігається в точці х=0. Тому область збіжності степеневого ряду містить точку нуль, тобто .

Теорема (теорема Абеля). Якщо степеневий ряд 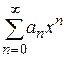збігається в точці 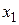, тоді 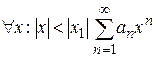– збігається абсолютно в точці .

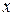Означення. Радіусом збіжності степеневого ряду 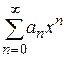називається значення величини 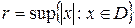, де 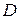– область збіжності степеневого ряду.

Означення. Інтервал 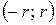називається інтервалом збіжності степеневого ряду, де – радіус збіжності степеневого ряду.

Теорема (теорема Коші-Адамара). Розглянемо степеневий ряд 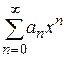. Позначимо 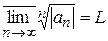, тоді

I)	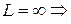II)	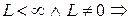III)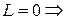
степеневий ряд розбігається при 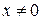,	1) 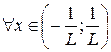даний ряд абсолютно збігається, 2) даний ряд розбігається,	степеневий ряд збігається на ,
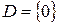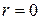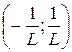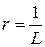тобто , ;	тобто – інтервал збіжності, а радіус збіжності ;	Тобто , .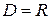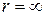

Наслідок. Формула для обчислення радіуса збіжності степеневого ряду : .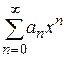

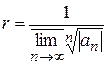Можна отримати іншу формулу за умови, що : .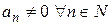

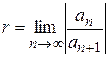Лема. Нехай – радіус збіжності степеневого ряду 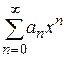, тоді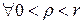 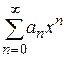– рівномірно збігається на .

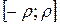Теорема (теорема про інтегрування степеневих рядів). Степеневий ряд 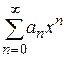можна почленно інтегрувати на 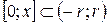( – радіус збіжності), крім того, радіус збіжності отриманого почленним інтегруванням степеневого ряду буде той самий, що і у вихідного ряду, тобто .

Теорема (теорема про диференціювання степеневих рядів). Степеневий ряд можна почленно диференціювати всередині інтервалу збіжності, при цьому отриманий почленним диференціюванням ряд має той самий радіус збіжності, що й вихідний ряд.

Наслідок. Степеневий ряд можна почленно диференціювати скільки завгодно разів. Всі ряди, отримані 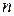-кратним диференціюваннями, будуть мати той самий радіус збіжності, що й вихідний ряд.

Переглядів: 1382