Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Закон великих чисел.

Припустимо, що відбувається п спостережень випадкової величини. Позначимо можливі значення випадкової величини, які вона приймає в спостереженнях (сукупність результатів спостережень назвемо випадковою вибіркою), через 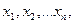де індекси означають номери спостережень.

Середня арифметична можливих результатів п спостережень

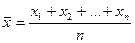
називатиметься середньою вибіркою.

Коли випадкова величина набуває тільки невід’ємне значення, математичне очікування, в певній мірі, характеризує її закон розподілу. Більшість величин з якими доводиться працювати в дійсності, є невід’ємними.

Виникає питання, чи можна оцінити ймовірність відхилення додатньої випадкової величини від математичного очікування.

Розглянемо приклад: Середня тривалість розмови по телефону на одній із АТС за даними ряду спостережень виявлена рівною 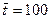сек. Чи можна отримати будь – яку інформацію про те, що серед розмов на цій АТС будуть мати місце розмови з тривалістю х, яка перевищує середню тривалість в k = 6 або більшість разів. Максимально можлива частота розмови 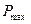з тривалістю 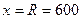сек і більше при середній тривалості в 100 сек мала місце в тому випадку, якщо б одні розмови були довжиною тільки 600 сек, а інші тільки - 0 сек. Тому в цьому випадку 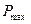можна визначити з співвідношення:

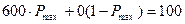сек,

Або в загальному випадку

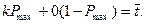
Знаходимо :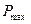

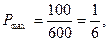
або в загальному випадку:

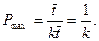
Таким чином, максимально можлива частота 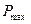розмов з тривалістю, яка в 6 разів перевищує середню тривалість рівна 1/6. це означає, що частка 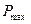буде тільки рівна або менша 1/6 (але не більша)

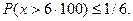
В загальному вигляді:

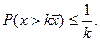
Останню нерівність називають нерівністю Чебишева.

Застосуємо нерівність Чебишева до квадрату відхилення середньої вибіркової:

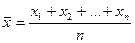
від її математичного очікування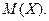

Отримаємо, що

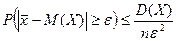
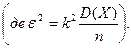
Яка б не була мала стала величина 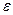, ймовірність того, що різниця між вибірковою середньою х і її математичним очікуванням 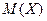за абсолютною величиною перевищить 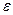, буде прямувати до 0 при 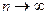. Дана нерівність носить назву закону великих чисел.

Розглянемо приклад застосування нерівності Чабишева.

Нехай ймовірність того, що на АТС відбулась телефонна розмова рівна р, а якщо ця телефонна розмова не відбулася, то 1-р.

Запишемо значення випадкової величини: 1 – розмова відбулася, 0 – розмова не відбулась.

Складемо закон розподілу для нашої випадкової величини:


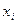
ймовірність випадкової величини	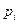р	1-р

Запишемо математичне очікування:

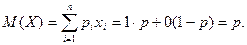
Знайдемо дисперсію, використовуючи формулу 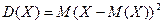. Запишемо значення .


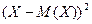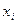
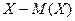
	1- р	0-р

Обчислюємо дисперсію:

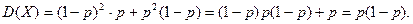
Якщо врахувати, що ймовірність того, що розмова відбулась р=0,5; то 1-р=0,5, тоді дисперсія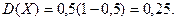

Врахуємо, що при достатньо великій кількості телефонних розмов на АТС середня вибіркова запишеться як

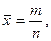
де п – число всіх спостережень за розмовами,

m – число спостережень, де розмова відбулась.

Підставимо значення 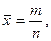математичного очікування М(х)=р; дисперсія 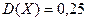в нерівності Чебишева

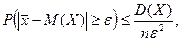
Отримаємо

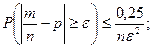
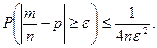
Цей вираз означає, що яка б не була мала постійна 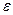, ймовірність р того, що різниця між середньою вибірковою 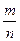і ймовірністю р перевищить 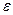, робиться близькою до нуля при достатньому числі спостережень п.

<== попередня сторінка	\|	наступна сторінка ==>
Формула повної ймовірності.	\|

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.