
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Похідна. Диференціювання функцій, заданих аналітично, параметрично та неявно, таблично, графічно.
Диференціальне числення функцій однієї змінної
ЛЕКЦІЯ № 10
Похідна. Диференціювання функцій, заданих аналітично, параметрично та неявно, таблично, графічно.
Навчальна мета: сформувати вміннядиференціювати функції, задані аналітично, параметрично та неявно, таблично, графічно;
Розвивальна мета: розвивати просторове уявлення, інтерес до предмета;
Виховна мета: виховувати організованість та дисципліну розумової праці.
План
1. Похідна функції
2. Геометричний зміст похідної.
3. Диференціювання функції.
4. Формули диференціювання елементарних функцій.
5. Похідна складної функції.
6. Функція задана параметричними рівняннями.
7. Функція задана неявно.
8. Похідна другого порядку.
9. Основні правила диференціювання функцій.
10. Похідною третього порядку.
11. Похідна n-го порядку.
12. Диференціал аргументу.
У випадку зіткнення автомобіля з перешкодою ступінь тяжкості травм водія і пасажирів визначається величиною миттєвої швидкості в точці зіткнення. У математиці значення швидкості зміни шляху в конкретній точці визначається поняттям “похідна функції”.
Похідною функції y = f (x) за аргументом x (швидкістю зміни функцій f (x) ) називається границя відношення приросту Δ f функції
(у нашому прикладі – приросту пройденого шляху) до приросту Δ x
її аргументу (у прикладі – до приросту часу) за умови, коли Δ x à 0:
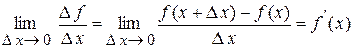 .
.
Для похідної використовуються такі позначення:
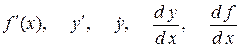 .
.
Отже, еквівалентними є такі позначення:
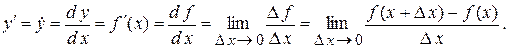
Геометрично похідна являє собою кутовий коефіцієнт дотичної лінії до графіка функції y = f (x) у точці x, тобто y¢ = tg a, де a – кут нахилу дотичної лінії (див. рис. 2.7).
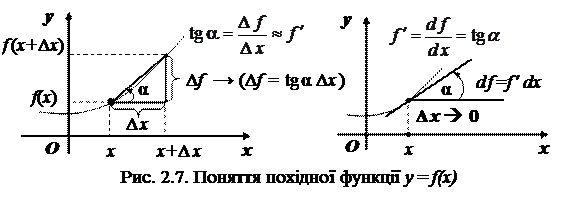 |
Диференціюванням функції y = f (x) називається процес відшукання похідної.
Для ілюстрації способу одержання формул диференціювання знайдемо похідну функції f (x) = (хn). Використовуючи визначення похідної
і формулу бінома Ньютона (див. додаток 3), одержимо:
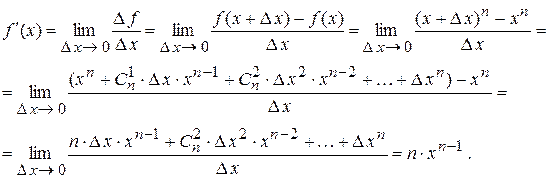
У підсумку виявляється, що (хn)¢= n хn–1. Наприклад (x2 )¢ = 2x. Якщо F ¢= j,то функцію F називають первісноюдля функції j.
У розглянутому прикладі для функції j = 2x первісною є F = x2.
Використаємо відзначену раніше еквівалентність нескінченно малих функцій (e x – 1) ~ x і знайдемо похідну ще однієї функції, що має широке застосування при описі динаміки економічних і фізичних процесів, f (x) = e x:
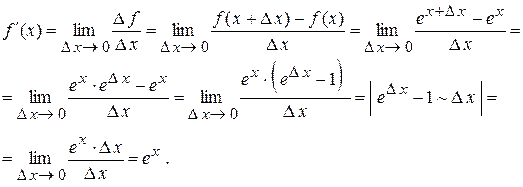
У підсумку виявилося, що операція узяття похідної від функції f (x) = e x не змінює аналітичного запису цієї функції, тобто тангенс кута нахилу дотичної лінії до будь-якої точки цієї функції дорівнює значенню цієї функції ( e x ) у точці побудови дотичної лінії.
Інші формули диференціювання елементарних функцій наведемо
в табл. 2.3 без виведення.
Якщо С – постійна величина, U(x) і V(x) – функції, що мають похідні, то справедливі правила, які наведені в табл. 2.4.
Пояснимо правила диференціювання, що мають найбільше застосування.
| Таблиця 2.3 | |||||
| Формули диференціювання елементарних функцій | |||||
| (С)¢ = 0 | 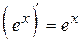
| 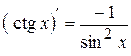
| |||
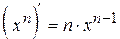
| 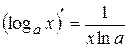
| 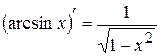
| |||
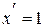
| 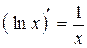
| 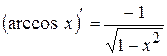
| |||
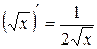
| 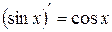
| 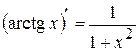
| |||
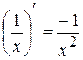
| 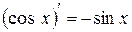
| 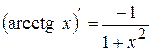
| |||
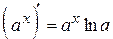
| 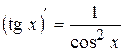
| 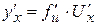
|
Якщо функція y = f (U) має похідну на U, а функція U = U(x) має похідну на х, то похідна складної функції дорівнює:
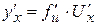 .
.
Якщо функція аргументу х задана параметричними рівняннями, то її похідна буде дорівнюватимє частці від ділення похідних кожної складової:
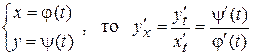 .
.
Якщо функція y задана неявно, тобто визначається з рівняння F (x, y) = 0, то для відшукання похідної y¢ диференціюють на х обох частин рівняння F (x, y) = 0, з огляду на те, що y є функція від х. Після цього
з отриманого рівняння першого ступеня щодо y¢ знаходиться похідна y¢.
Інший спосіб відшукання похідної від неявно заданої функції F (x, y) = 0 – це використання відомого співвідношення [13]:
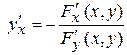 .
.
Похідною другого порядку (другою похідною) функції y = f (х) називається похідна від її першої похідної y¢¢ = (y¢)¢.
| Таблица 2.4 | |||
| Основні правила диференціювання функцій | |||
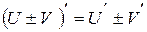
| 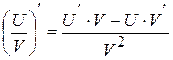
| ||
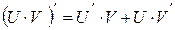
| 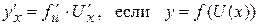
| ||
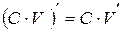
| 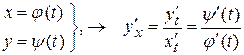
|
Позначається друга похідна одним із таких символів:
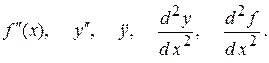
Похідною третього порядку (третьою похідною) функції y = f (х) називається похідна від її другої похідної y¢¢¢ = (y¢¢)¢.
Похідноюn-гопорядку (n-ю похідною) функції y = f (х) називається похідна від її похідної (n – 1)-гопорядку: y(n) = (y(n–1))¢.
Обчислюється похідна n-го порядку шляхом послідовного диференціювання функції. Позначається n-а похідна одним із таких символів:
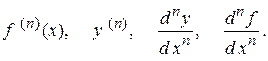
Диференціалом аргументу називається (див. рис. 2.7 ) приріст аргументу dх = Δ х.
Диференціал (першого порядку) функції y = f (х) позначається символом dy або df і дорівнює (див. рис. 2.7) добутку першої похідної функції на диференціал аргументу:
dy = y¢∙dх; (df = f ¢∙dх ) 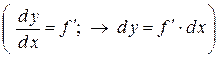 .
.
Якщо приріст Δ х аргументу х малий (за абсолютною величиною), то:
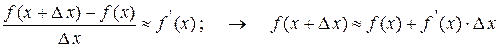 .
.
Остання рівність використовується для наближених обчислень значень функції.
Приклади. Застосовуючи формули і правила диференціювання, знайти похідні таких функцій:
1) 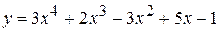 .
.
Розв’язання. 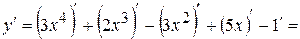
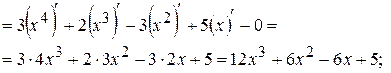
2)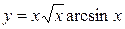 .
.
Розв’язання. Скористаємося тим, що 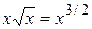 ,
,
тоді 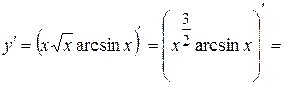
 ;
;
3)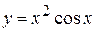 . Розв’язання.
. Розв’язання.
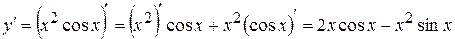 ;
;
4) 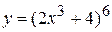 .
.
Розв’язання. Позначимо 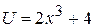 , тоді y = U 6 і (див. табл. 2.4, п. 5)
, тоді y = U 6 і (див. табл. 2.4, п. 5)
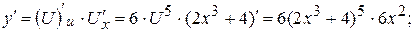
5) 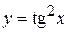 . Розв’язання.
. Розв’язання. 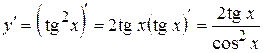 ;
;
6) 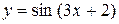 .
.
Розв’язання. 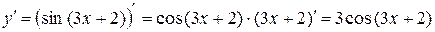 ;
;
7) 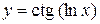 .
.
Розв’язання.
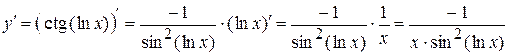 ;
;
8) 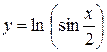 .
.
Розв’язання.
 ;
;
9) 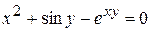 .
.
Розв’язання. Диференціюємо рівняння за х:
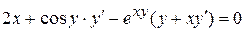 , звідки
, звідки 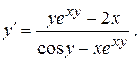
Застосовуючи інший варіант розв’язання, відповідно до формули
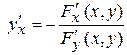 , знаходимо:
, знаходимо: 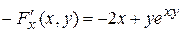 ;
;
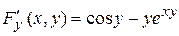 , що дозволяє одержати той же результат;
, що дозволяє одержати той же результат;
10) 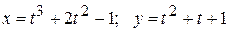 .
.
Розв’язання. 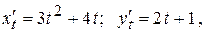 тому
тому  .
.
Приклади. Знайти похідні другого порядку.
1) 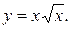
Розв’язання. Скористаємося тим, що 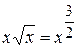 . Тоді
. Тоді
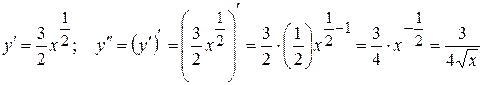 ;
;
2) 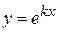 .
.
Розв’язання. 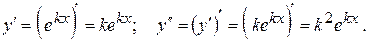
Приклад. Знайти диференціал функції 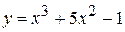 .
.
Розв’язання.  .
.
Приклад. Обчислити наближене значення 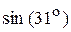 .
.
Розв’язання. Уважаючи, що 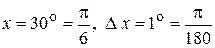 , використаємо наближену рівність f (х + Δ х )» f (х) + f ¢(x)∙Δ х.
, використаємо наближену рівність f (х + Δ х )» f (х) + f ¢(x)∙Δ х.
Тоді 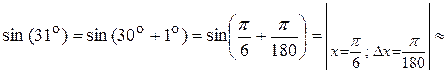
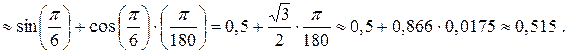
| <== попередня сторінка | | | наступна сторінка ==> |
| Хімічні властивості. | | | Домашне завдання |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |