Загальна схема генетичних алгоритмів

У концептуальному плані загальна схема генетичних алгоритмів досить проста. Спочатку генерується початкова популяція особин (індивідуумів, хромосом), тобто деякий ряд розв'язків задачі. Як правило, це робиться випадково. Потім необхідно змоделювати розмноження всередині цієї популяції. Для цього випадково підбираються кілька пар індивідуумів, проводиться схрещування хромосом у кожній парі, а отримані нові хромосоми поміщають у популяцію нового покоління. У генетичному алгоритмі зберігається засадний принцип природного добору: чим пристосованіший індивідуум (чим більше відповідне йому значення цільової функції), тим з більшою ймовірністю він буде брати участь у схрещуванні.

Потім моделюються мутації в кількох випадково вибраних особинах нового покоління, тобто змінюються деякі гени. Після цього стара популяція частково або повністю знищується і ми переходимо до розгляду наступного покоління. Популяція наступного покоління в більшості реалізацій генетичних алгоритмів містить стільки ж особин, скільки й початкова, але внаслідок відбору пристосованість (значення цільової функції) у ній в середньому вища. Операція доведення кількості особин поточної популяції до початково визначеної величини називається редукцією. Описані процеси відбору, схрещування і мутації повторюються вже Для цієї нової популяції.

У кожному наступному поколінні буде спостерігатися виникнення абсолютно нових розв'язків задачі. Серед них будуть як погані, так і кращі, але завдяки процедурі добору кількість кращих розв'язків буде зростати. Зауважимо, що в природі не буває абсолютних гарантій, і навіть найпристосованіший тигр може загинути від пострілу мисливця, не залишивши потомства. Імітуючи еволюцію в комп'ютері, можна уникати подібних небажаних подій і завжди зберігати життя кращому з індивідуумів поточно-⁰ покоління. Така методика називається «стратегією елітизму», коли в наступне покоління відбираються особини з найкращими показниками.

Описана послідовність дій за реалізації генетичних алгоритмів може перетворюватися в різні програмні реалізації залежно від типу розв'язуваної задачі і вибраних для цього підходів. Зокрема, в низці випадків може вводитися інша, ніж описана вище, єрархія базових понять, наприклад, кожний індивідуум може характеризуватися низкою хромосом, котрі, у свою чергу, містять різні типи генів. Пояснимо на прикладі.

Нехай розглядається завдання вибору плану вкладення коштів у вибрані наперед N інвестиційних проектів, причому потрібно визначити обсяги вкладень коштів у кожний проект так, щоб загальний їх обсяг в усі проекти не перевищував величину D, а вибраний критерій ефективності, наприклад рівень рентабельності інвестицій (прибуток на капітал, ROI — Return on Investment), набував максимального значення. Розв'язуючи цю задачу за генетичним алгоритмом, вважатимемо, що кожен індивідуум — це інвестиційний план, який містить N хромосом, кожна з яких являє собою вектор із нулів та одиниць — двійковий вираз обсягу вкладень у даний проект. Якщо довжина хромосоми дорівнює вісьмом двійковим розрядам, то потрібне попереднє нормування всіх чисел на інтервалі від 0 до 255 (усього значень 2⁸). Такі хромосоми називаються безперервними і уможливлюють подання значень довільних числових параметрів.

Мутації безперервних хромосом випадковим способом змінюють у них один біт (ген), впливаючи у такий спосіб на значення параметра. Кросовер також можна здійснювати стандартно, об'єднуючи частини відповідних хромосом (з однаковими номерами) різних індивідуумів. Особливістю цієї задачі є те, що загальний обсяг капіталу, що інвестується, фіксований і дорівнює D. Очевидно, що із-за мутацій і схрещувань можна отримувати розв'язки, для реалізації яких потрібний капітал, більший або менший ніж D. У генетичному алгоритмі використовується спеціальний механізм аналізування таких розв'язків, що дає змогу враховувати обмеження типу «сумарний капітал = D " за підрахунку пристосованості індивідуума. У процесі еволюції особини з суттєвим порушенням зазначених обмежень «вимирають». Унаслідок дії алгоритму отриманий розв'язок за сумарним капіталом може не дорівнювати точно, але бути близьким до заданої величини D. У процесі роботи генетичного алгоритму оцінюється значення цільової функції для кожного плану і здійснюється операція редукції для всієї популяції.

Цю саму задачу можна подати і в іншій генетичній інтерпретації, якщо ввести умову, що кожний із інвестиційних проектів aбо цілком приймається, або відхиляється. Тоді кожний варіант плану (хромосому) можна подати у вигляді послідовності з N нулів та одиниць, причому, якщо на цьому місці в хромосомі стоїть одиниця, то це означає, що і-й проект (і - 1, 2, ..., ЛО включений у план, а якщо нуль — не включений. Популяція складається із кількох варіантів планів. Визначення допустимості планів і оцінювання їх за вибраними критеріями проводиться аналогічно.

У загальному вигляді стратегію отримання рішень за допомогою генетичних алгоритмів можна реалізувати такими кроками:

1) ініціалізуйте популяцію;

2) виберіть батьків для репродукції і оператори мутації і кросовера;

3) виконайте операції, щоб згенерувати проміжну популяцію індивідуумів і оцінити їхні придатності;

4) виберіть членів популяції для отримання нової генерації

(версії);

5) повторюйте кроки 1—З, поки не буде досягнуте деяке правило зупинки.

На рис. 2 показана узагальнена схема реалізації генетичного алгоритму. До його основних характеристик належать: розмір популяції, оператор кросовера і ймовірність його використання, оператор мутації і її ймовірність, оператор селекції, оператор редукції, правило (критерій) зупинки процесу виконання генетичного алгоритму. Оператори селекції, кросовера, мутації і редукції ще називають генетичними операторами.

Критерієм зупинки процесу здійснення генетичного алгоритму може бути одна з трьох подій:

^• сформовано задану користувачем кількість поколінь;

• популяція досягла заданої користувачем якості (наприклад, значення якості всіх особин перевищило задану порогову величину);

• досягнутий деякий рівень збіжності. Тобто особини в популяції стали настільки подібними, що дальше їх поліпшення відсувається надзвичайно повільно, і тому продовження здійснення ітерацій генетичного алгоритму стає недоцільним.

Після завершення роботи генетичного алгоритму з кінцевої популяції вибирається та особина, яка дає максимальне (або мінімальне) значення цільової функції і, отже, є результатом здійснення генетичного алгоритму. За рахунок того, що кінцева популяція краща, ніж початкова, отриманий результат являє собою поліпшене рішення.

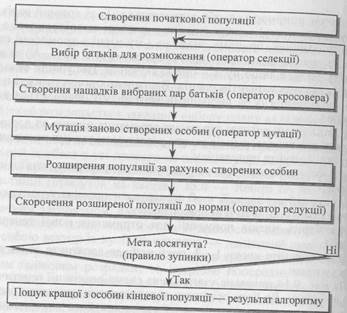
Рисунок 2. Узагальнена схема реалізації генетичного алгоритму

1.3.Доступне програмне забезпечення генетичних алгоритмів

Генетичні алгоритми нині можна застосовувати в різних галузях. їх успішно використовують для розв'язування низки великих і економічно важливих задач у бізнесі і в інженерних розробках. З їх допомогою були розроблені промислові проектні рішення, що уможливили багатомільйонну економію витрат. Фінансові компанії широко використовують ці засоби у разі прогнозування розвитку фінансових ринків для управління пакетами цінних паперів. Нарівні з іншими методами генетичні алгоритми, зазвичай, використовуються для оцінювання значень безперервних параметрів моделей великих розмірностей, для розв'язування комбінаторних задач, для задач з оптимізації, що містять одночасно безперервні і дискретні параметри. Іншою галуззю їх застосування є використання в системах добування нових знань із великих баз даних, створення і навчання стохастичних мереж, навчання нейронних мереж, оцінювання параметрів у задачах багатовимірного статистичного аналізу, отримання початкових даних для виконання інших алгоритмів пошуку і оптимізації. Все це зумовило зростання заінтересованості фірм-розробників комерційного програмного забезпечення стосовно генетичних алгоритмів, що в кінцевому результаті привело до появи на ринку багатьох програмних продуктів такого виду.

Незважаючи на те, що розв'язання конкретної оптимізаційної задачі часто потребує побудови генетичного алгоритму з унікальними значеннями параметрів, низка базових властивостей цих алгоритмів залишається постійною за розв'язання абсолютно різних задач. Тому здебільшого для реалізації конкретного генетичного алгоритму не потрібно створювати окремий програмний продукт.

Опишемо кілька прикладів програмного забезпечення, що дає змогу реалізовувати широкий набір генетичних алгоритмів, які можна застосовувати для розв'язування найрізноманітніших задач. Змінними параметрами генетичних алгоритмів у таких додатках, зазвичай, є різні значення ймовірностей, розмір популяції і низка специфічних властивостей алгоритму. Проте реалізація генетичних операторів, як правило, єдина для всіх алгоритмів і прихована від користувача.

Пакет Evolver 4.0 компанії Palisade Corp. Пакет Evolver являє собою доповнення до програми MS Excel версій 5.0 і 7.0. При цьому Excel використовується як засіб опису початкових даних алгоритму і розрахунків у процесі його виконання. У процесі установки Evolver додає в Excel додаткову панель інструментів, яка забезпечує доступ до пакета. Якщо Evolver не запущений для виконання, то панель інструментів не відображається. У разі запуску Evolver додаток Excel запускається автоматично.

Пакет GeneHunter 1.0 компанії Ward System Group. Пакет GeneHunter багато чим схожий з пакетом Evolver. Він також є надбудовою над MS Excel версій 5.0 і 7.0 і запускається з меню «Сервіс». Цей пакет русифікований і має низку додаткових настройок для генетичних алгоритмів: включення стратегій елітизму й різноманітності. Поля вікна GeneHunter практично такі самі як і в Evolver. Однак його вікно має низку відмінностей. Для установки параметрів алгоритму служить кнопка «Параметри...». Параметри генетичного алгоритму не зберігаються автоматично з файлом Eхсel. Для збереження параметрів служить кнопка «Модель», після натиснення на яку з'являється відповідне діалогове вікно.

Пакет Genetic Training Option (GTO) компанії California Scientific Software. Пакет GTO є додатковою утилітою, що поставляється для нейропакета BrainMaker виробництва компанії «California Scientific Software». Він застосовується як для побудови нейронних мереж, так і для поліпшення створеної за допомогою BrainMaker мережі. Але в обох випадках окремо від BrainMaker використовуватися не може.

Генетичні алгоритми складні для створення, але прості в застосуванні — потребують від користувача тільки формалізації задачі й формування початкових даних. Така ситуація багато в чому сприяє розширенню галузей застосування генетичних алгоритмів.

Лабораторна робота № 1
Методи генетичного пошуку

<== попередня сторінка	\|	наступна сторінка ==>
I. Генетичні алгоритми	\|	Мета роботи

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.