• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Пропорційний відбір

Даний вид відбору складається з наступної послідовності кроків.

Крок 1. Обчислити пристосованість кожної особини f_j.

Крок 2. Знайти середню пристосованість у популяції f_ср як середнє арифметичне значень пристосованості всіх особин:

.

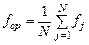Крок 3. Для кожної особини обчислити відношення .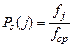

Крок 4. Залежно від величини P_s( j) сформувати масив особин, допущених до схрещування.

Формування масиву допущених до схрещування особин (крок 4) можна здійснити двома шляхами:

Перший шлях (стохастичний залишковий відбір): якщо P_s( j) > 1, то особина вважається добре пристосованою та допускається до схрещування.

Наприклад, якщо дріб P_s( j) = 2,36, то дана особина має подвійний шанс на схрещування й буде мати ймовірність рівну 0,36 третього схрещування. Якщо ж пристосованість дорівнює 0,54, то особина візьме участь у єдиному схрещуванні з імовірністю 0,54.

Другий шлях: після знаходження відносини P_s( j) відбувається відбір (із заміщенням) всіх N особин для подальшої генетичної обробки, відповідно до величини P_s( j).

Найпростіший пропорційний відбір – рулетка – відбирає особини за допомогою N запусків рулетки.

Колесо рулетки містить по одному сектору для кожного члена популяції. Розмір j-го сектору пропорційний відповідній величині P_s( j). Особина одержує можливість створення нащадків, якщо випадково згенероване число в межах від 0 до 2p попадає в сектор, що відповідає цій особини. При такому відборі члени популяції з більш високою пристосованістю з більшою ймовірністю будуть частіше вибиратися, чим особини з низькою пристосованістю.

При реалізації відбору рулеткою доцільно замінити колесо рулетки інтервалом [0;1] у зв'язку з тим, що в такому випадку немає необхідності обчислювати ширину кожного сектора – у цьому випадку кожній особині ставиться у відповідність напівінтервал [x_j-1; x_j), де x_j-1 – x_j = P_s( j), а x₀ = 0 (при цьому x_N = 1). У наступне покоління переходить особина з номером j, де j: x_{r nd} Î [x_j-1; x_j), а число x_{r nd} повертається щораз випадковою функцією з рівномірним розподілом щільності ймовірності на відрізку [0;1].

Схема рулетки може давати дуже великі помилки, у тому розумінні, що кінцеве число нащадків даної особини може сильно відрізнятися від очікуваного. Кінцеве число наближається до очікуваного тільки в популяціях дуже більших розмірів.

Переглядів: 484