• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Бінарні відношення

Приклад. Знайти області визначення і значень відношення .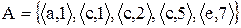

Рішення: Область визначення заданого відношення 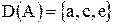, а область значень ‑ .

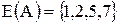Приклад. Нехай 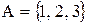, 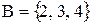. Знайти декартовий добуток множин та 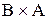. Записати , , .

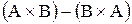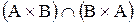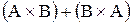Рішення: ;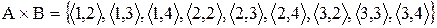

;

;

;

.

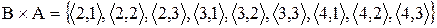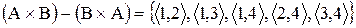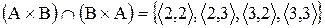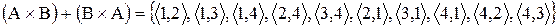Приклад. Нехай 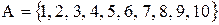. Задати в явному виді (списком) і матрицею відношення 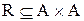, якщо відношення 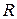означає “бути строго більше”.

Рішення: Відношення 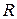містить всі впорядковані пари елементів 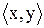з :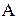

.

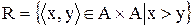Список відношення 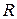виглядає в такий спосіб:

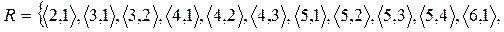
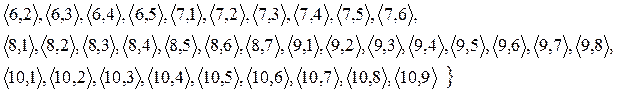
Матриця відношення :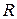

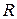
Приклад. Нехай 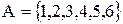і відношення 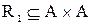є множина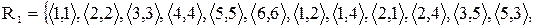 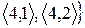. Які властивості має задане відношення?

Рішення. Побудуємо матрицю відношення:

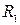
Відношення 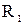рефлексивне, тому що для кожного 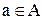, 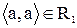. Головна діагональ матриці відношення 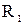містить одиниці.

Відношення 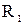не є антирефлексивне, тому що з умови 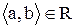не треба 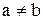, наприклад, 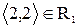, але .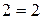

Розглянувши всі можливі випадки методом безпосереднього перескладання (табл. 1а) можна показати, що відношення 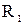симетрично. Крім того, матриця відношення 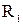симетрична щодо головної діагоналі.

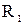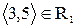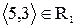не є антисиметричне, тому що і , але .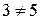

Скориставшись методом безпосереднього перескладання (табл. 1б) можна також показати, що відношення 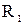транзитивне.

Таблиця 1

(а) (б)

№					№
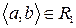
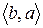
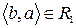
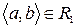
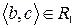
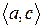
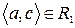
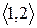
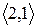
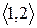
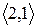
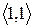
			так						так
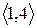
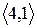
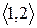
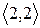
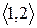
			так						так
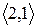
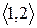
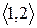
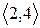
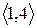
			так						так
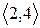
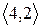
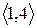
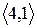
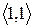
			так						так
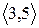
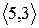
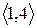
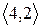
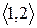
			так						так
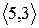
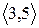
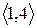
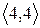
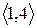
			так						так
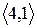
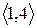
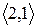
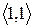
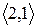
			так						так
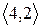
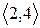
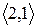
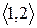
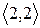
			так						так
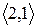
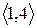
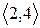
									так
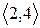
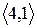
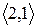
									так
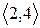
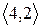
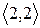
									так
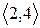
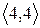
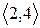
									так
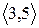
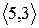
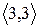
									так
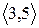
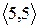
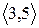
									так
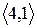
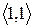
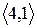
									так
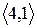
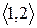
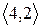
									так
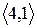
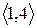
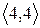
									так
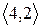
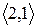
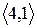
									так
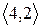
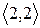
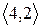
									так
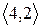
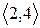
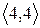
									так
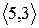
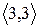
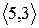
									так
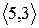
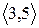
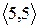
									так

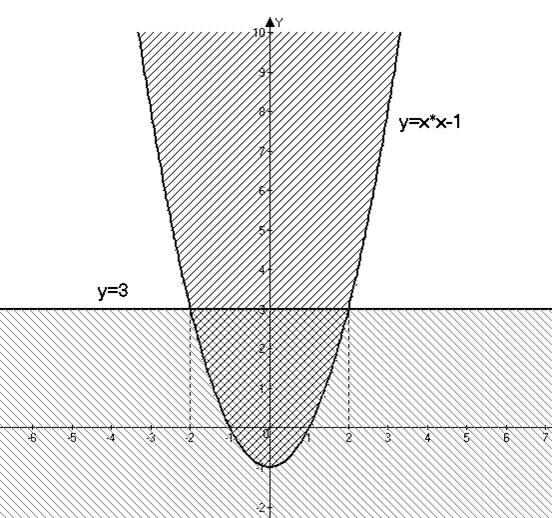
Приклад. Знайти області визначення і значень відношення. Накреслити його графік.

А = {(x,y)│y ≤ x² -1, y ≤ 3}

Рішення: Область визначення заданого відношення 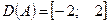, а область значень – .

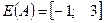ЗАВДАННЯ ГРАФІЧНО-РОЗРАХУНКОВОЇ РОБОТИ

1.1 Запишіть множину А за допомогою характеристичної властивості.

1. А={7, 14, 21, 28, 35, 42, …}

2. А={-30, -20, -10, 0, 10, 20, 30, 40}

3. А={11, 22, 33, 44, 55, 66, …}

4. А={-25, -20, -15, -10, -5, 0, 5, 10, 15}

5. А={3, 6, 9, 12, 15, 18, …}

6. А={-8, -6, -4, -2, 0, 2, 4, 6, 8, 10, 12}

7. А={к, о, г, а, і, л}

8. А={літо, зима, осінь, весна}

9. А={1, 3, 5, 7, 9, 11, 13, …}

10. А={-9, -6, -3, 0, 3, 6, 9, 12, 15}

11. А={е, л, а, к, т, р, і, к, о, н}

12. А={4, 8, 16, 20, 24, 28, 32, …}

13. А={1, 4, 9, 16, 25, 36, 49, 64, 81, …}

14. А={-18, -12, -6, 0, 6, 12, 18, 24, 30, 36}

15. А={с, х, к, а, н, і, е, м, о, т}

16. А={-64, -56, -48, -40, -32, -24, -16, -8}

17. А={10, 20, 30, 40, 50, 60, …}

18. А={е, л, к, т, р, а, д, і, я, н, в, и, о, м, ю}

19. А={-400, -300, -200, -100, 0, 100, 200, 300, 400, 500}

20. А={9, 18, 27, 36, 45, 54, 63, …}

21. А={-21, -14, -7, 0, 7, 14, 21, 28, 35, 42, 49, 56}

22. А={р, н, а, я, в, п, о, г, м, у}

23. А={-39, -26, -13, 0, 13, 26, 39}

24. А={-44, -33, -22, -11, 0, 11, 22, 33, 44, 55, 66}

25. А={5, 10, 15, 20, 25, 30, 35, …}

1.2 Знайдіть доповнення до множини А, якщо універсум містить усі натуральні числа, що не більші за 10.

1) А={x|x² -5 x +6= 0}

2) А={x|x² -12 x +20= 0}

3) А={x|x² -6 x +8= 0}

4) А={x|x² -11 x +18= 0}

5) А={x|x² -4 x +4= 0}

6) А={x|x² -7 x +10= 0}

7) А={x|x² -11 x +10= 0}

8) А={x|x² -8 x +12= 0}

9) А={x|x² -10 x +9= 0}

10) А={x|x² -11 x +18= 0}

11) А={x|x² -9 x +8= 0}

12) А={x|x² -10 x +16= 0}

13) А={x|x² -8 x +7= 0}

14) А={x|x² -9 x +14= 0}

15) А={x|x² -7 x +6= 0}

16) А={x|x² -7 x +12= 0}

17) А={x|x² -6 x +5= 0}

18) А={x|x² -8 x +15= 0}

19) А={x|x² -5 x +4= 0}

20) А={x|x² -9 x +18= 0}

21) А={x|x² -4 x +3= 0}

22) А={x|x² -10 x +21= 0}

23) А={x|x² -3 x +2= 0}

24) А={x|x² -11 x +24= 0}

25) А={x|x² -2 x +1= 0}

1.3 Знайдіть переріз, об’єднання, та різницю множин А і В.

1) А={x|x² -5 x +6= 0}, В={x|x² - x -6= 0}

2) А={x|x² -12 x +20= 0}, В={x|x² +5x -14= 0}

3) А={x|x² -6 x +8= 0}, В={x|x² +4 x -32= 0}

4) А={x|x² -11 x +18= 0}, В={x|x² +4 x -45= 0}

5) А={x|x² -4 x +4= 0}, В={x|x² +9 x -22= 0}

6) А={x|x² -7 x +10= 0}, В={x|x² -2 x -15= 0}

7) А={x|x² -11 x +10= 0}, В={x|x² -9 x -10= 0}

8) А={x|x² -8 x +12= 0}, В={x|(x² -4)( x -6)= 0}

9) А={x|x² -10 x +9= 0}, В={x|(x² -1)( x -9)= 0}

10) А={x|x² -11 x +18= 0}, В={x|(x² -81)( x -2)= 0}

11) А={x|x² -9 x +8= 0}, В={x|(x² -1)( x -8)= 0}

12) А={x|x² -10 x +16= 0}, В={x|(x² -64)( x -2)= 0}

13) А={x|x² -8 x +7= 0}, В={x|x² +6 x -7= 0}

14) А={x|x² -9 x +14= 0}, В={x|(x² -49)( x +6)= 0}

15) А={x|x² -7 x +6= 0}, В={x|(x² -36)( x -6)= 0}

16) А={x|x² -7 x +12= 0}, В={x|x² - x -6= 0}

17) А={x|x² -6 x +5= 0}, В={x|(x² -9) (x² -16)= 0}

18) А={x|x² -8 x +15= 0}, В={x|(x² -9) (x² -25)= 0}

19) А={x|x² -5 x +4= 0}, В={x|(x² -1) (x² -16)= 0}

20) А={x|x² -9 x +18= 0}, В={x|(x² -9) (x² -36)= 0}

21) А={x|x² -4 x +3= 0}, В={x|(x² -9) (x² -1)= 0}

22) А={x|x² -10 x +21= 0}, В={x|(x² -9) (x² -49)= 0}

23) А={x|x² -3 x +2= 0}, В={x|(x² -4) (x² -1)= 0}

24) А={x|x² -11 x +24= 0}, В={x|(x² -9) (x² -64)= 0}

25) А={x|x² -2 x +1= 0}, В={x|(x² -x² -42)= 0}

1.4 Виконайте операції над множинами А і В: 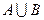, , 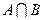, , 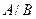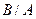якщо:

1) A=[-3;20), B=(0;12]

2) A=[2;10), B=(1;4]

3) A=[6;13), B=(7;15]

4) A=[-1;6) B=(5;7]

5) A=(8;10) B=[3;6]

6) A=[-2;6) B=(0;7]

7) A=[3;8) B=(-3;5]

8) A=[-1;6) B=[2;4]

9) A=[0;8) B=(3;5]

10) A=[-6;8) B=(6;13]

11) A=[3;8) B=(1;7]

12) A=[3;4) B=(-6;8]

13) A=(7;16) B=(4;12]

14) A=[-8;16) B=(13;20]

15) A=(-6;13) B=(2;16]

16) A=[7;8) B=(-4;7]

17) A=[7;23) B=(4;14]

18) A=(-16;8) B=(-8;16]

19) A=[-21;7) B=(3;14]

20) A=[13;16) B=[7;21]

21) A=[5;8) B=(-7;13]

22) A=(7;9) B=(1;6]

23) A=[-9;5) B=[-3;1]

24) A=[5;12) B=(5;12]

25) A=(-3;3) B=[-1;2]

1.5 Спростіть функцію F.

1)

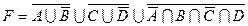
2)

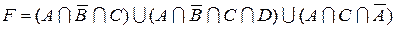
3)

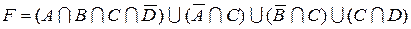
4)

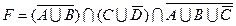
5)

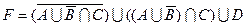
6)

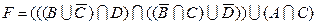
7)

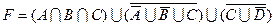
8)

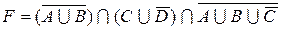
9)

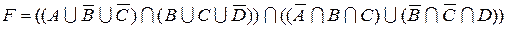
10)

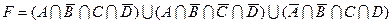
11)

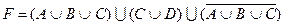
12)

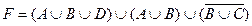
13)

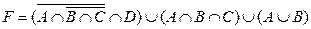
14)

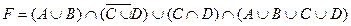
15)

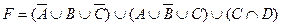
16)

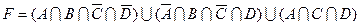
17)

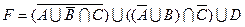
18)

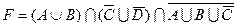
19)

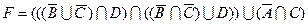
20)

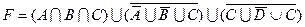
21)

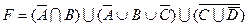
22)

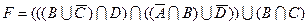
23)

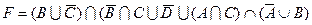
24)

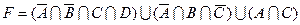
25)

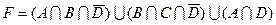
1.6Запишіть формулу для діаграми Венна, яку зображено на рисунку:

1.		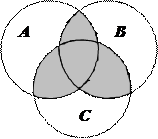2.		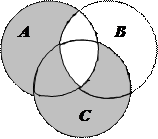3.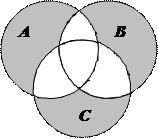
4.		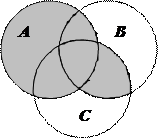5.		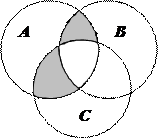6.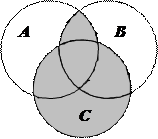
7.		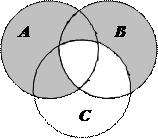8.		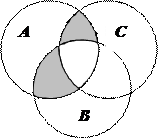9.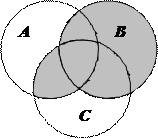
10.		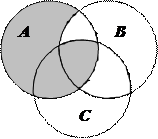11.		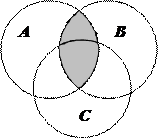12.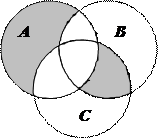
13.		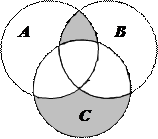14.		15.
16.		17.		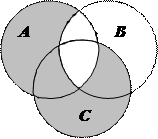18.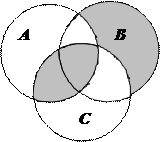
19.		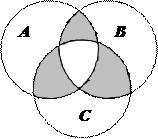20.		21.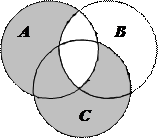
22.		23.		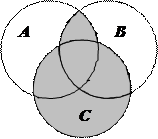24.
25.

1.7 Для заданої формули побудуйте діаграму Венна.

1)

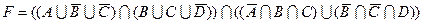
2)

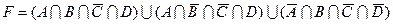
3)

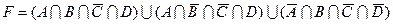
4)

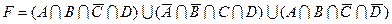
5)

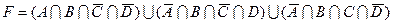
6)

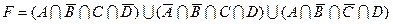
7)

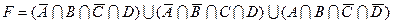
8)

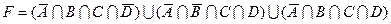
9)

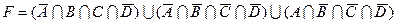
10)

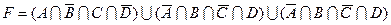
11)

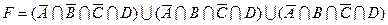
12)

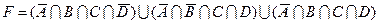
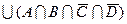
13)

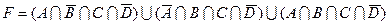
14)

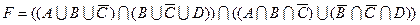
15)

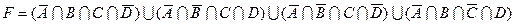
16)

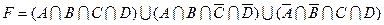
17)

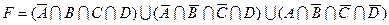
18)

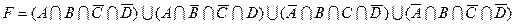
19)

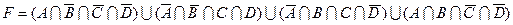
20)

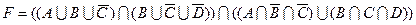
21)

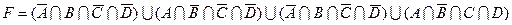
22)

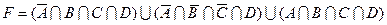
23)

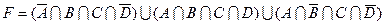
24)

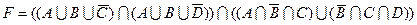
25)

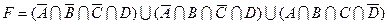
2.1 Знайдіть області визначення і значень відношень. Проілюструйте відображення множини D у множину E. Задайте відношення матрицею.

1)

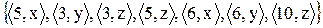
2)

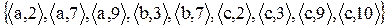
3)

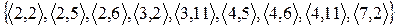
4)

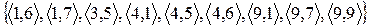
5) {(2;1),(1;1),(3;1),(5;2),(5;4),(6;1),(6;9),(6;7),(6;10),(6;5)}

6) {(2, 5), (2, 1), (2, 0), (4,5), (4, 1), (4, 0), (6, 5), (6, 1), (6, 0), (8, 5)}

7) {(5, 2), (5, 4), (5, 6), (5, 8), (5, 10), (1, 2), (1, 4), (1, 6)}

8) {(1, 8), (1, 10), (0, 2), (0, 4), (0, 6), (0, 8), (0, 10)}

9) {(6, 1), (6, 0), (8, 5), (8, 1), (8, 0), (10, 5), (10, 1), (10, 0)}

10) {(x,6), (y, 7), (z, 2), (z, 4), (y, 6), (x, 8), (a, 3) (a,5)}

11) {(5, 5), (1, 9), (6, 6), (3, 7), (1, 9), (1, 3), (11, 1)}

12) {(9, 9), (1, 3), (2, 2), (8, 3), (7, 6), (4, 8), (4, 10)}

13) {(2, 8), (11, 10), (5, 3), (4, 7), (9, 5), (4, 2), (6, 11) (1,8)}

14) {(1, x), (y, 5), (1, z), (5, x), (7, y), (8, z), (9, z)}

15) {(11, 7), (9, 12), (5, 1), (9, 3), (8, 5), (9, 6), (1, 1)}

16) {(5, 3), (5, 5), (7, 8), (1, 2), (9, 9), (2, 7), (1, 10)}

17) {(a, 9), (b, 10), (b, 2), (c, 3), (a, 5), (c,7), (a, 4)}

18) {(12, 8), (11, 3), (5, 2), (3, 3), (7, 6), (8, 9), (4, 5)}

19) {(7, 10), (5, 11), (4, 8), (4, 3), (1, 8), (11, 8), (7, 9)}

20) {(5, 5), (1, 9), (3, 6), (2, 4), (1, 9), (1, 3), (10, 1)}

21) {(7, 5), (2, 3), (8, 9), (1, 10), (11, 9), (5, 7), (6, 4)}

22) {(2, 9), (11, 4), (5, 4), (7, 2), (1, 1), (4, 7), (3, 5)}

23) {(5, 5), (1, 9), (2, 6), (3, 3), (1, 2), (4, 5), (5, 9)}

24) {(10, 9), (7, 1), (8, 8), (1, 2), (9, 3), (8, 2), (3, 11)}

25) {(a, 7), (a, 9), (b, 2), (b, 5), (c, 1), (c, 7), (c, 10)}

2.2 Знайдіть області визначення і значень відношень. Накресліть їх графіки.

1) ;

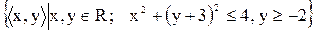2) ;

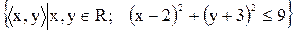3) ;

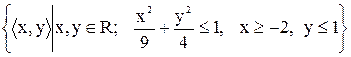4) ;

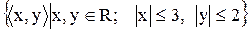5) ;

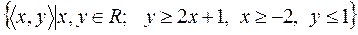6) ;

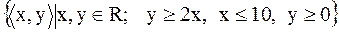7) ;

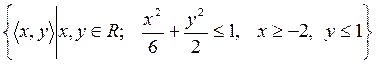8) ;

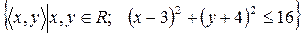9) ;

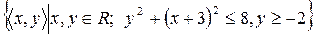10) ;

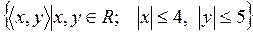11) ;

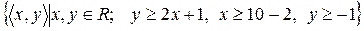12) ;

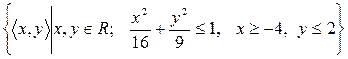13) ;

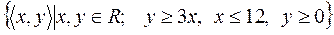14) ;

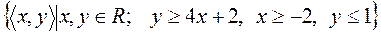15) ;

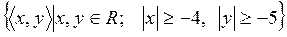16)

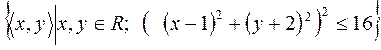
17) ;

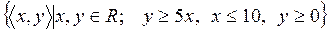18) ;

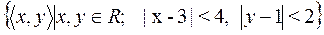19) ;

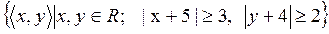20) ;

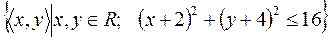21) ;

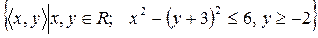22) ;

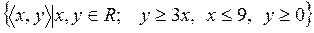23) ;

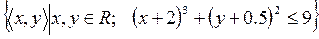24) ;

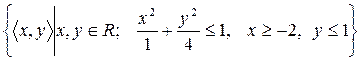25) ;

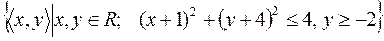2.3

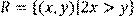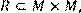
1) Для відношення , 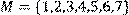побудувати матрицю відношення, знайти область визначення Dom(R), область значень Im(R), доповнююче R, обернене відношення. Визначити, чи виконуються для даного відношення властивості рефлексивності, симетричності, антисимметричності, транзитивності, повноти.

2) Для відношення R = {(x, y)|(x + y) – парне} ,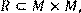

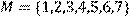
побудувати матрицю відношення, знайти область визначення Dom(R), область значень Im(R), доповнююче R, обернене відношення. Визначити, чи виконуються для даного відношення властивості рефлексивності, симетричності, антисимметричності, транзитивності, повноти.

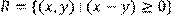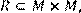
3) Для відношення , 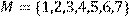побудувати матрицю відношення, знайти область визначення Dom(R), область значень Im(R), доповнююче R, обернене відношення. Визначити, чи виконуються для даного відношення властивості рефлексивності, симетричності, антисимметричності, транзитивності, повноти.

4) Для відношення R = {(x, y)|x, y мають один і той же залишок від ділення на 2} , 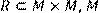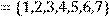побудувати матрицю відношення, знайти область визначення Dom(R), область значень Im(R), доповнююче R, обернене відношення. Визначити, чи виконуються для даного відношення властивості рефлексивності, симетричності, антисимметричності, транзитивності, повноти.

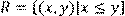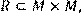
5) Для відношення , 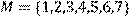побудувати матрицю відношення, знайти область визначення Dom(R), область значень Im(R), доповнююче R, обернене відношення. Визначити, чи виконуються для даного відношення властивості рефлексивності, симетричності, антисимметричності, транзитивності, повноти.

6) Для відношення R = {(x, y)|(x + 2y) – парне } , 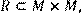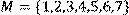побудувати матрицю відношення, знайти область визначення Dom(R), область значень Im(R), доповнююче R, обернене відношення. Визначити, чи виконуються для даного відношення властивості рефлексивності, симетричності, антисимметричності, транзитивності, повноти.

7) Для відношення 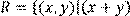кратне ,

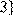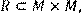
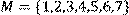
побудувати матрицю відношення, знайти область визначення Dom(R), область значень Im(R), доповнююче R, обернене відношення. Визначити, чи виконуються для даного відношення властивості рефлексивності, симетричності, антисимметричності, транзитивності, повноти.

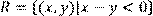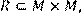
8) Для відношення , 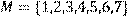побудувати матрицю відношення, знайти область визначення Dom(R), область значень Im(R), доповнююче R, обернене відношення. Визначити, чи виконуються для даного відношення властивості рефлексивності, симетричності, антисимметричності, транзитивності, повноти.

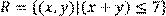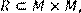
9) Для відношення , 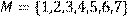побудувати матрицю відношення, знайти область визначення Dom(R), область значень Im(R), доповнююче R, обернене відношення. Визначити, чи виконуються для даного відношення властивості рефлексивності, симетричності, антисимметричності, транзитивності, повноти.

10) Для відношення R = {(x, y) | x і y взаємно прості} , 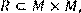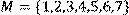побудувати матрицю відношення, знайти область визначення Dom(R), область значень Im(R), доповнююче R, обернене відношення. Визначити, чи виконуються для даного відношення властивості рефлексивності, симетричності, антисимметричності, транзитивності, повноти.

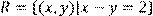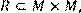
11) Для відношення , 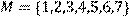побудувати матрицю відношення, знайти область визначення Dom(R), область значень Im(R), доповнююче R, обернене відношення. Визначити, чи виконуються для даного відношення властивості рефлексивності, симетричності, антисимметричності, транзитивності, повноти.

12) Для відношення R = {(x, y)|x дільник y} , 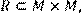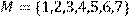побудувати матрицю відношення, знайти область визначення Dom(R), область значень Im(R), доповнююче R, обернене відношення. Визначити, чи виконуються для даного відношення властивості рефлексивності, симетричності, антисимметричності, транзитивності, повноти.

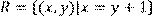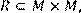
13) Для відношення , 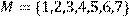побудувати матрицю відношення, знайти область визначення Dom(R), область значень Im(R), доповнююче R, обернене відношення. Визначити, чи виконуються для даного відношення властивості рефлексивності, симетричності, антисимметричності, транзитивності, повноти.

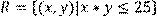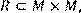
14) Для відношення , 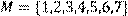побудувати матрицю відношення, знайти область визначення Dom(R), область значень Im(R), доповнююче R, обернене відношення. Визначити, чи виконуються для даного відношення властивості рефлексивності, симетричності, антисимметричності, транзитивності, повноти.

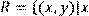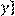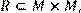
15) Для відношення кратне , 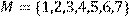побудувати матрицю відношення, знайти область визначення Dom(R), область значень Im(R), доповнююче R, обернене відношення. Визначити, чи виконуються для даного відношення властивості рефлексивності, симетричності, антисимметричності, транзитивності, повноти.

16) Для відношення R={(x, y)|(x + y) – непарне},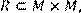

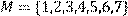
побудувати матрицю відношення, знайти область визначення Dom(R), область значень Im(R), доповнююче R, обернене відношення. Визначити, чи виконуються для даного відношення властивості рефлексивності, симетричності, антисимметричності, транзитивності, повноти.

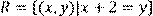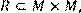
17) Для відношення , 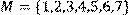побудувати матрицю відношення, знайти область визначення Dom(R), область значень Im(R), доповнююче R, обернене відношення. Визначити, чи виконуються для даного відношення властивості рефлексивності, симетричності, антисимметричності, транзитивності, повноти.

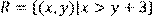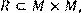
18) Для відношення , 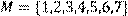побудувати матрицю відношення, знайти область визначення Dom(R), область значень Im(R), доповнююче R, обернене відношення. Визначити, чи виконуються для даного відношення властивості рефлексивності, симетричності, антисимметричності, транзитивності, повноти.

19) Для відношення R={(x, y)|(x + y) – парне} ,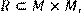

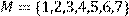
побудувати матрицю відношення, знайти область визначення Dom(R), область значень Im(R), доповнююче R, обернене відношення. Визначити, чи виконуються для даного відношення властивості рефлексивності, симетричності, антисимметричності, транзитивності, повноти.

20) Для відношення R={(x ,y)|(x + 3y)–парне} ,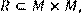

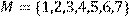
побудувати матрицю відношення, знайти область визначення Dom(R), область значень Im(R), доповнююче R, обернене відношення. Визначити, чи виконуються для даного відношення властивості рефлексивності, симетричності, антисимметричності, транзитивності, повноти.

21) Для відношення 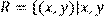мають один і той же залишок від ділення на 3} , 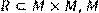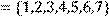побудувати матрицю відношення, знайти область визначення Dom(R), область значень Im(R), доповнююче R, обернене відношення. Визначити, чи виконуються для даного відношення властивості рефлексивності, симетричності, антисимметричності, транзитивності, повноти.

22) Для відношення 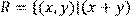кратне ,

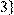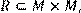
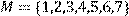
побудувати матрицю відношення, знайти область визначення Dom(R), область значень Im(R), доповнююче R, обернене відношення. Визначити, чи виконуються для даного відношення властивості рефлексивності, симетричності, антисимметричності, транзитивності, повноти.

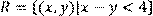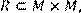
23.)Для відношення , 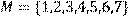побудувати матрицю відношення, знайти область визначення Dom(R), область значень Im(R), доповнююче R, обернене відношення. Визначити, чи виконуються для даного відношення властивості рефлексивності, симетричності, антисимметричності, транзитивності, повноти.

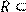
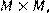
24) Для відношення R={(x, y)|x, y мають спільний дільник, відмінний від 1} , 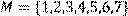побудувати матрицю відношення, знайти область визначення Dom(R), область значень Im(R), доповнююче R, обернене відношення. Визначити, чи виконуються для даного відношення властивості рефлексивності, симетричності, антисимметричності, транзитивності, повноти.

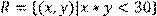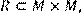
25) Для відношення , 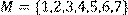побудувати матрицю відношення, знайти область визначення Dom(R), область значень Im(R), доповнююче R, обернене відношення. Визначити, чи виконуються для даного відношення властивості рефлексивності, симетричності, антисимметричності, транзитивності, повноти.

Переглядів: 2753