
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
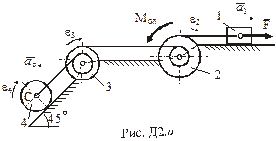
Приклад Д-2
Механічна система (рис.Д2.а) складається з вантажу 1, ступінчастих шківів 2 і 3 (маса шківів рівномірно розподілена по зовнішніх ободах) та однорідного циліндричного котка 4.Тіла зв’язані між собою нерозтяжними нитками, намотаними на шківи. Горизонтальна площина гладенька, коток котиться без ковзання.
Система рухається під дією сили 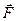 . При русі на шків 2 діє постійний момент сил опору
. При русі на шків 2 діє постійний момент сил опору  . Визначити силу натягу нитки, що утримує вантаж 1.
. Визначити силу натягу нитки, що утримує вантаж 1.
 Дано:
Дано:
m1 = 4 кг, m2 = 3 кг,
m3 = 5кг, m4 =2кг,
R2 = 0,2м, r2 = 0,1м,
R3 = 0,3м, r3 = 0,1м,
M оп= 0,6 Нм, F = 200H.
Визначити: силу натягу нитки, що утримує вантаж 1.
Розв’язування.
Розглянемо рух незмінної механічної системи, що складається з тіл 1, 2, 3 і 4. Система рухається під дією сили 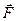 . В залежності від цього покажемо напрямок прискорень всіх тіл системи.
. В залежності від цього покажемо напрямок прискорень всіх тіл системи.
Для того, щоб застосувати динамічні рівняння руху тіл, роз’єднаємо систему на окремі тіла та зобразимо їх вільними (рис.Д2.б,в,г,д). Зобразимо активні сили, діючі на тіла. В’язі, накладені на тіла, замінимо їх реакціями. Реакції ниток, що з’єднують тіла, покажемо вздовж ниток у напрямку від тіла (бо нитки розтягнуті). Згідно із законом рівності дії та протидії маємо:
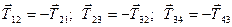 Вибираємо системи координат для кожного тіла так, щоб проекції прискорень на обрані осі були додатними.
Вибираємо системи координат для кожного тіла так, щоб проекції прискорень на обрані осі були додатними.
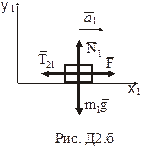 Розглянемо тіло 1 (рис.Д2.б). На нього діють: рушійна сила
Розглянемо тіло 1 (рис.Д2.б). На нього діють: рушійна сила 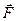 ; сила ваги
; сила ваги 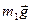 ; реакція площини
; реакція площини 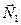 та сила реакції нитки
та сила реакції нитки 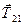 , що з’єднує тіла 1 і 2 (подвійні індекси треба читати як сила, діюча з боку тіла 2 на тіло 1). Вибираємо систему координат
, що з’єднує тіла 1 і 2 (подвійні індекси треба читати як сила, діюча з боку тіла 2 на тіло 1). Вибираємо систему координат  таким чином, щоб прискорення
таким чином, щоб прискорення 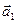 збігалося б за напрямом з віссю
збігалося б за напрямом з віссю 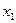 .
.
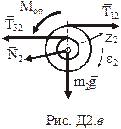 Розглянемо тіло 2 (рис.Д2.в). На нього діють: момент опору
Розглянемо тіло 2 (рис.Д2.в). На нього діють: момент опору  ; сила ваги
; сила ваги 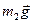 ; реакція підшипника
; реакція підшипника 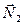 ; сили реакцій ниток
; сили реакцій ниток 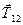 та
та 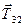 , що з’єднують тіло 2 з тілами 1 і 3. Вісь обертання
, що з’єднують тіло 2 з тілами 1 і 3. Вісь обертання 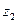 спрямуємо від нас за напрямком вектора кутового прискорення
спрямуємо від нас за напрямком вектора кутового прискорення 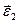 .
.
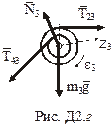 Розглянемо тіло 3 (рис.Д2.г). На нього діють: сила ваги
Розглянемо тіло 3 (рис.Д2.г). На нього діють: сила ваги 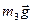 ; реакція підшипника
; реакція підшипника 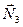 ; сили реакцій ниток
; сили реакцій ниток 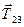 та
та 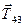 , що з’єднують тіло 3 з тілами 2 і 4. Вісь обертання
, що з’єднують тіло 3 з тілами 2 і 4. Вісь обертання 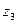 спрямуємо від нас за напрямком вектора кутового прискорення
спрямуємо від нас за напрямком вектора кутового прискорення  .
.
 Розглянемо тіло 4 (рис.Д2.д). На нього діють: сила ваги
Розглянемо тіло 4 (рис.Д2.д). На нього діють: сила ваги 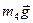 ; реакція площини (по якій котиться коток без ковзання) розкладається на дві складові: нормальну
; реакція площини (по якій котиться коток без ковзання) розкладається на дві складові: нормальну 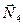 , перпендикулярну до площини, і силу зчеплення
, перпендикулярну до площини, і силу зчеплення 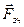 , яка спрямована вздовж площини; та сила реакції нитки
, яка спрямована вздовж площини; та сила реакції нитки 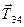 , що з’єднує тіло 4 з тілом 3. Вибираємо систему координат
, що з’єднує тіло 4 з тілом 3. Вибираємо систему координат  таким чином, щоб прискорення
таким чином, щоб прискорення  збігалося за напрямом з віссю
збігалося за напрямом з віссю 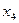 , вісь обертання
, вісь обертання 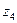 спрямуємо від нас за напрямком вектора кутового прискорення
спрямуємо від нас за напрямком вектора кутового прискорення 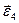 .
.
Запишемо динамічне рівняння руху кожного тіла, що входить до системи.
Для тіла 1: 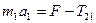 (2.1)
(2.1)
Для тіла 2: 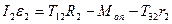 (2.2)
(2.2)
Для тіла 3: 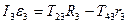 (2.3)
(2.3)
Для тіла 4: 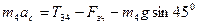 (2.4)
(2.4)
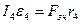 (2.5)
(2.5)
Систему рівнянь (2.4) і (2.5) замінимо одним, виключивши з них 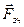 :
:
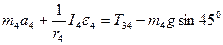 (2.6)
(2.6)
Силу реакції нитки 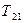 можна знайти з рівняння (2.1). Для цього треба знати, з яким прискоренням
можна знайти з рівняння (2.1). Для цього треба знати, з яким прискоренням 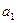 рухається тіло 1. Прискорення будь якого тіла можна знайти з динамічного рівняння руху механічної системи, яке можна отримати з рівнянь (2.1) - (2.3) і (2.6), виключивши з них сили реакції ниток. Спочатку з’єднаємо рівняння (2.1) і (2.2).
рухається тіло 1. Прискорення будь якого тіла можна знайти з динамічного рівняння руху механічної системи, яке можна отримати з рівнянь (2.1) - (2.3) і (2.6), виключивши з них сили реакції ниток. Спочатку з’єднаємо рівняння (2.1) і (2.2).
Ураховуючи, що 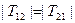 , помножимо рівняння (2.1) на
, помножимо рівняння (2.1) на 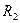 та додамо до рівняння (2.2), отримаємо:
та додамо до рівняння (2.2), отримаємо:
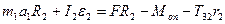 (2.7)
(2.7)
Враховуючи, що 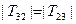 маємо з рівнянь (2.3) та (2.7):
маємо з рівнянь (2.3) та (2.7):
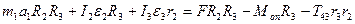 (2.8)
(2.8)
Остаточно з рівнянь (2.8) та (2.6), враховуючи, що 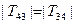 , отримаємо динамічне рівняння руху механічної системи:
, отримаємо динамічне рівняння руху механічної системи:
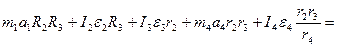
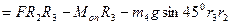 (2.9)
(2.9)
Щоб визначити прискорення вантажу 1, виразимо всі прискорення тіл системи через 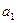 :
:
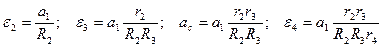 (2.10)
(2.10)
Моменти інерції визначимо за формулами:
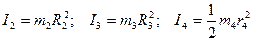 (2.11)
(2.11)
Підставимо (2.10) і (2.11) в (2.9) та винесемо прискорення 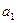 за дужки:
за дужки:

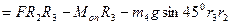 (2.12)
(2.12)
Підставимо числові значення та знайдемо прискорення вантажу 1:
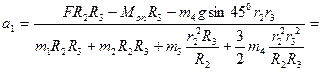
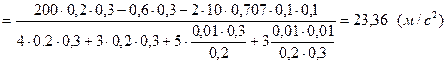
З рівняння (2.1) знайдемо силу реакції нитки, що утримує вантаж 1:
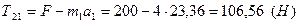
Відповідь: 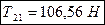
Завдання Д-3. Теорема про зміну кінетичної енергії
Умова завдання. Механічна система складається із вантажів 1 і 2 (коефіцієнт тертя вантажів з площиною 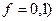 , циліндричного однорідного котка 3 та ступінчастих шківів 4 і 5 з радіусами ступіней
, циліндричного однорідного котка 3 та ступінчастих шківів 4 і 5 з радіусами ступіней 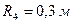 ,
,  ,
, 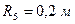 ,
, 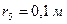 (масу кожного шківа вважати розподіленою по зовнішньому ободу) (рис.Д3.0– Д3.9, табл.Д3). Якщо маса тіла 2 m2 = 0 , груз 2 на рисунку не зображати; шківи 4 і 5 та вантаж 1 завжди входять в систему. Тіла зв'язані між собою нерозтяжними нитками, намотаними на шківи; ділянки ниток паралельні відповідним площинам. Коток 3 котиться без ковзання. Точка
(масу кожного шківа вважати розподіленою по зовнішньому ободу) (рис.Д3.0– Д3.9, табл.Д3). Якщо маса тіла 2 m2 = 0 , груз 2 на рисунку не зображати; шківи 4 і 5 та вантаж 1 завжди входять в систему. Тіла зв'язані між собою нерозтяжними нитками, намотаними на шківи; ділянки ниток паралельні відповідним площинам. Коток 3 котиться без ковзання. Точка  є центром мас котка 3.
є центром мас котка 3.
Під дією сили F =f(s), що залежить від переміщення вантажу 1, система починає рухатись. В початковий момент часу система знаходилась в спокої. На шківи 4 та 5 діють постійні за величиною моменти опору, що дорівнюють відповідно 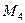 та
та  .
.
Визначити.В момент часу, коли переміщення точки прикладання сили 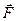 дорівнює
дорівнює 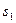 , визначити указані в стовпцях «Знайти» (табл.Д3) швидкості.
, визначити указані в стовпцях «Знайти» (табл.Д3) швидкості.
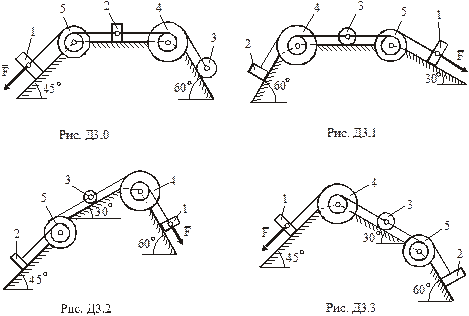
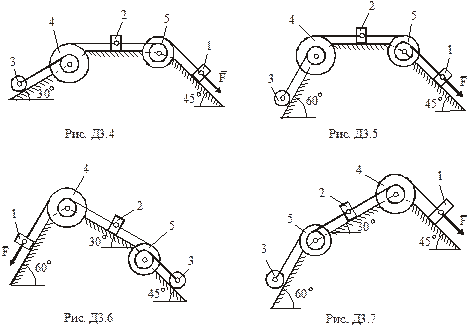
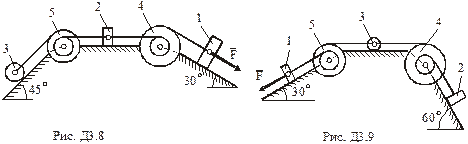
Табл.Д3.
| № умови | 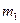 , кг , кг
| 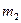 , кг , кг
| 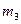 , кг , кг
| 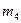 , кг , кг
| 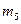 , кг , кг
| 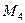 , Н·м , Н·м
|  , Н·м , Н·м
| 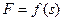 , Н , Н
| 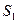 , м , м
| Визна-чити |
| 0,8 | 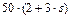
| 1,0 | 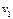
| |||||||
| 0,6 | 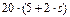
| 1,2 | 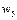
| |||||||
| 0,4 | 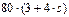
| 0,8 | 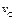
| |||||||
| 0,3 | 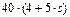
| 0,6 | 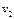
| |||||||
| 0,6 | 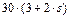
| 1,4 | 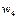
| |||||||
| 0,9 | 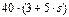
| 1,6 | 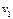
| |||||||
| 0,8 | 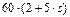
| 1,0 | 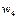
| |||||||
| 0,6 | 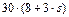
| 0,8 | 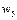
| |||||||
| 0,3 | 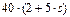
| 1,6 | 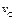
| |||||||
| 0,4 | 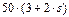
| 1,4 | 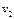
|
Теоретичне обґрунтування : [5] § 121 – 124 ; [6] Розд.III. Гл.4. § 5 – 7 ;
[7] § 58, 61, 65 – 69 ; [8]; [9]; [10]; [12]; [14].
Методичні вказівки. Завдання Д-3 на тему «Теорема про зміну кінетичної енергії механічної системи» в інтегральній формі.
Для незмінних механічних систем (тобто 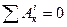 ) теорема має вид:
) теорема має вид:
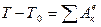 , (Д3.1)
, (Д3.1)
де Т - кінетична енергія системи в кінцевому положенні;
Т0 - кінетична енергія системи в початковому положенні;
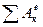 - сума робіт зовнішніх сил, діючих на систему на заданому її переміщенні;
- сума робіт зовнішніх сил, діючих на систему на заданому її переміщенні;
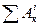 - сума робіт внутрішніх сил, діючих в системі на заданому її переміщенні.
- сума робіт внутрішніх сил, діючих в системі на заданому її переміщенні.
Кінетична енергія системи дорівнює сумі кінетичних енергій тіл системи, тобто:
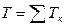 (Д3.2)
(Д3.2)
В залежності від того, який рух виконує тверде тіло, кінетична енергія визначається:
1) при поступальному русі 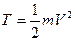 , (Д3.3)
, (Д3.3)
де m - маса тіла; V – швидкість тіла.
2) при обертальному русі тіла навколо нерухомої осі z
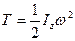 , (Д3.4)
, (Д3.4)
де Iz - осьовий момент інерції тіла відносно осі z;
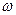 - кутова швидкість тіла.
- кутова швидкість тіла.
3) при плоскому русі в площині Сxy
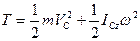 , (Д3.5)
, (Д3.5)
де m – маса тіла; VC – швидкість центру мас тіла; ICz - осьовий момент інерції тіла відносно осі Сz; 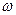 - кутова швидкість тіла.
- кутова швидкість тіла.
Момент інерції однорідного котка: 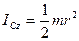 .
.
Момент інерції кільця радіуса R : 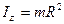 .
.
Робота змінної сили F =f(s) :
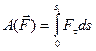 , (Д3.6)
, (Д3.6)
де 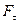 - проекція сили на напрямок переміщення точки прикладення сили.
- проекція сили на напрямок переміщення точки прикладення сили.
Робота постійної сили 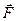 :
:
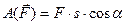 , (Д3.7)
, (Д3.7)
де 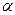 - кут між силою
- кут між силою 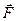 і напрямком переміщення точки прикладення сили.
і напрямком переміщення точки прикладення сили.
Робота пари сил з моментом  :
:
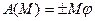 , (Д3.8)
, (Д3.8)
де 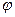 - кут повороту тіла. Знак „+” беремо, якщо момент М і кут
- кут повороту тіла. Знак „+” беремо, якщо момент М і кут 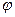 однаково спрямовані, та „ – ”, якщо вони спрямовані протилежно.
однаково спрямовані, та „ – ”, якщо вони спрямовані протилежно.
| <== попередня сторінка | | | наступна сторінка ==> |
| Визначити | | | Приклад Д-3 |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |