
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Розв’язування.
Розглянемо рух механічної системи, що складається з вала 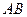 , стержня
, стержня 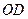 та вантажу
та вантажу 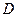 . Для визначення невідомих реакцій застосуємо принцип Д’Аламбера. Проведемо осі
. Для визначення невідомих реакцій застосуємо принцип Д’Аламбера. Проведемо осі 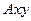 , що обертаються разом з валом, таким чином, щоб стержень знаходився в площині
, що обертаються разом з валом, таким чином, щоб стержень знаходився в площині 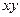 , та зобразимо діючі на систему зовнішні сили: сили ваги
, та зобразимо діючі на систему зовнішні сили: сили ваги 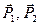 , складові
, складові 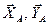 реакції підп’ятника і реакцію
реакції підп’ятника і реакцію 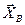 підшипника (рис.Д4.б).
підшипника (рис.Д4.б).
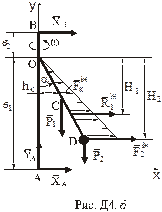 За принципом Д’Аламбера прикладемо сили інерції елементів стержня та вантажу, вважаючи його матеріальною точкою. Враховуючи, що вал обертається рівномірно
За принципом Д’Аламбера прикладемо сили інерції елементів стержня та вантажу, вважаючи його матеріальною точкою. Враховуючи, що вал обертається рівномірно 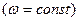 , елементи стержня мають тільки нормальні прискорення
, елементи стержня мають тільки нормальні прискорення 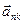 , спрямовані до осі обертання, чисельно:
, спрямовані до осі обертання, чисельно:
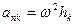 ,
,
де 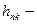 відстань елемента від осі.
відстань елемента від осі.
Тоді сили інерції 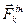 будуть спрямовані від осі обертання і чисельно:
будуть спрямовані від осі обертання і чисельно:
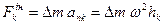 ,
,
де 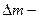 маса елемента.
маса елемента.
Оскільки всі 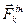 пропорційні
пропорційні 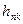 , то епюра цих паралельних сил є трикутник і їх можна замінити рівнодійною
, то епюра цих паралельних сил є трикутник і їх можна замінити рівнодійною 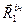 , лінія дії якої проходить через центр ваги цього трикутника, тобто на відстані
, лінія дії якої проходить через центр ваги цього трикутника, тобто на відстані 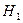 від вершини
від вершини 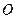 , де
, де 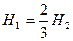 (
( 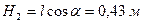 , тобто
, тобто 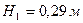 ) .
) .
Але, як звісно, рівнодійна будь якої системи дорівнює її головному вектору, а чисельно головний вектор сил інерції стержня:
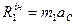 ,
,
де 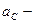 прискорення центра мас стержня.
прискорення центра мас стержня.
Як і будь-який елемент стержня, центр його мас має тільки нормальне прискорення:
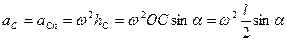
Таким чином отримаємо:
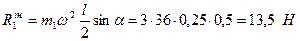
Аналогічно, сила інерції 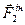 вантажу спрямована від осі обертання, а чисельно:
вантажу спрямована від осі обертання, а чисельно:
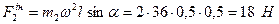 .
.
Всі діючі на систему сили і сили інерції знаходяться в одній площині 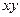 , тому і реакції підп’ятника
, тому і реакції підп’ятника 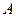 і підшипника
і підшипника 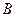 також знаходяться в цій площині, що було враховано при їх зображенні.
також знаходяться в цій площині, що було враховано при їх зображенні.
За принципом Д’Аламбера, прикладені активні сили, сили реакції та сили інерції складають зрівноважену систему сил. Таким чином, для отриманої плоскої системи сил , складемо три рівняння умовної рівноваги:
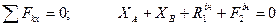 (4.1)
(4.1)
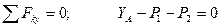 (4.2)
(4.2)
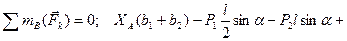
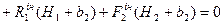 (4.3)
(4.3)
Підставимо числові значення, та знайдемо невідомі реакції. Через те, що 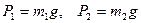 , приймаючи
, приймаючи 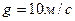 , з рівняння (4.2) знайдемо
, з рівняння (4.2) знайдемо 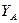 :
:
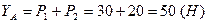 .
.
З рівняння (4.3) знайдемо 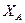 :
:
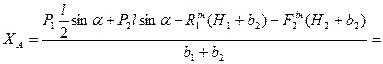
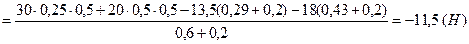
Підставимо отримане 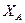 в рівняння (4.1) і знайдемо
в рівняння (4.1) і знайдемо  :
:
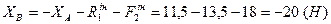 .
.
Відповідь:
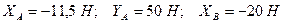 . Знаки вказують на те, що сили
. Знаки вказують на те, що сили 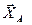 та
та 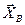 спрямовані протилежно показаним на рис. Д4.б
спрямовані протилежно показаним на рис. Д4.б
Завдання Д-5. Загальне рівняння динаміки
Умова завдання. Механічна система складається з однорідних ступінчастих шківів 1 і 2, обмотаних нерозтяжними нитками, вантажів 3 – 6, прикріплених до цих ниток, та невагомого блока (рис. Д5.0 – Д5.9, табл. Д5). Система рухається у вертикальній площині під дією сил ваги та пари сил з моментом  , прикладеної до одного з шківів. Радіуси ступенів шківа 1 дорівнюють:
, прикладеної до одного з шківів. Радіуси ступенів шківа 1 дорівнюють: 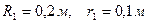 , а шківа 2 –
, а шківа 2 – 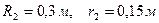 ; радіуси інерції відносно осей обертання дорівнюють відповідно
; радіуси інерції відносно осей обертання дорівнюють відповідно 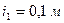 та
та  . Вага тіл
. Вага тіл  задана в табл. Д5. Вантажі, вага яких дорівнює нулю, на рисунку не зображати, шківи 1 і 2 зображати завжди.
задана в табл. Д5. Вантажі, вага яких дорівнює нулю, на рисунку не зображати, шківи 1 і 2 зображати завжди.
Визначити. Прискорення вантажу, що має найбільшу вагу, нехтуючи тертям.
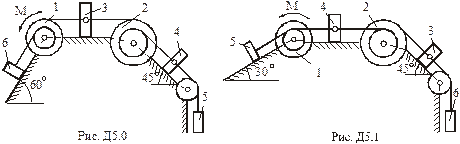
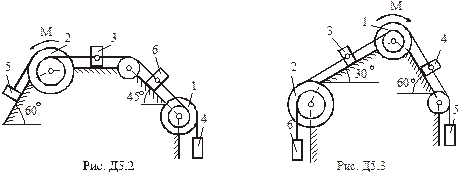
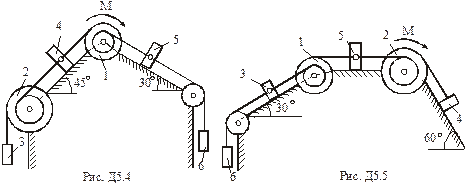
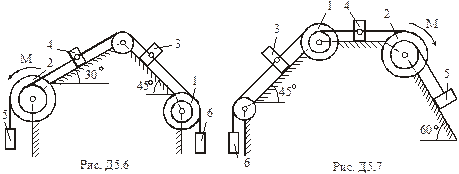
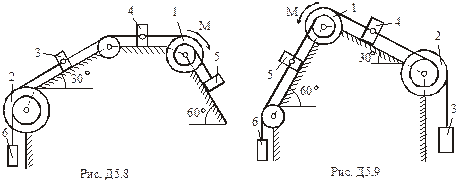
Табл. Д5
| № умови | 
| 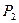 , , 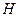
| 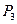 , , 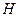
| 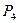 , , 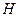
| 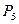 , , 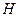
| 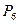 , , 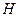
| 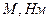
|
Теоретичне обґрунтування : [5] § 137 – 141; [6] Розд.III. Гл.6. § 1 – 3 , 8;
[7] § 112, 117, 118 ; [8]; [9]; [12]; [13] .
Методичні вказівки. Завдання Д-5 на тему «Загальне рівняння динаміки». Для систем з геометричними, стаціонарними ідеальними в’язями означене рівняння має вигляд:
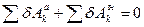 , (Д5.1)
, (Д5.1)
де 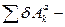 сума можливих робіт активних сил, що діють на систему;
сума можливих робіт активних сил, що діють на систему; 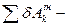 сума можливих робіт сил інерції.
сума можливих робіт сил інерції.
(У наведених вище сумах під можливою роботою розуміється робота сил на якомусь можливому переміщенні системи).
Сили інерції точок, з яких складаються тверді тіла, можна звести до головного вектора та головного моменту сил інерції відносно вибраного центру зведення (в динаміці за центр зведення беруть точку  - центр мас тіла). Для тіл, що виконують поступальний, обертальний або плоский рухи головний вектор і головний момент сил інерції визначаються за правилами.
- центр мас тіла). Для тіл, що виконують поступальний, обертальний або плоский рухи головний вектор і головний момент сил інерції визначаються за правилами.
Для тіла, що виконує поступальний рух:
- головний вектор 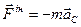 , головний момент
, головний момент 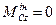 , (Д5.2)
, (Д5.2)
де 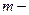 маса тіла,
маса тіла,  прискорення центру мас тіла.
прискорення центру мас тіла.
Головний вектор сил інерції та прискорення центру мас спрямовані протилежно.
Для тіла, що виконує обертальний рух навколо нерухомої центральної осі:
- головний вектор 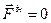 , головний момент
, головний момент 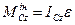 , (Д5.3)
, (Д5.3)
де  осьовий момент інерції,
осьовий момент інерції, 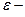 кутове прискорення тіла.
кутове прискорення тіла.
Головний момент сил інерції та кутове прискорення спрямовані протилежно.
Для тіла, що виконує плоский рух:
- головний вектор 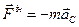 , головний момент
, головний момент 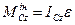 , (Д5.4)
, (Д5.4)
Головний вектор і головний момент сил інерції спрямовані протилежно відповідним прискоренням.
| <== попередня сторінка | | | наступна сторінка ==> |
| Приклад Д-4 | | | Приклад Д-5 |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |