Електростатичного поля

Для математичного моделювання електростатичного поля використовується той факт, що електричне поле стаціонарного струму в середовищі зі слабкою провідністю завжди є потенціальним. Це дає можливість використати електричне поле стаціонарного струму в середовищі зі слабкою провідністю для моделювання електростатичного поля заряджених тіл у вакуумі.

Роль заряджених тіл у моделювання виконують електроди, форма яких відповідає натуральним тілам, що виконані в певному масштабі (найчастіше збільшеному). Взаємне розміщення електродів має бути таким самим, як і в приладі, що моделюються. На електроди подається напруга, що дорівнює або пропорційна напрузі на електродах приладу, який моделюється. За виконання цих умов електричне поле між електродами матиме таку саму конфігурацію, як і те поле, що моделюється, відрізняючись від нього тільки чисельним значенням напруженості.

Якщо між електродами розмістити середовище зі слабкою провідністю, то конфігурація електричного поля зміниться. Проте за певних умов подібних змін можна уникнути. Які ж ці умови?

Розподіл поля у просторі задається рівнянням Максвелла для електричного поля. Розв’язок цих рівнянь, який визначає закон розподілу напруженості поля, залежить як від вигляду самих рівнянь, так і від граничних умов. Покажемо, що вигляд рівнянь Максвелла не зміниться, якщо замінити непровідне середовище на провідне.

Як відомо, густина електричного струму j всередині провідника задовільняє рівняння неперервності:

divj = 0.

Використовуючи закон Ома в диференціальній формі і враховуючи, що питома електропровідність середовища є величиною сталою (σ = сonst), одержимо:

divj = div(σЕ) = σ divЕ = 0,

Звідки

divЕ = 0. (2.1)

За відсутності змінного у часі магнітного поля виконується умова

rotE = 0.(2.2)

Таким чином, електричне поле сталого струму задовольняє рівняння (2.1) і (2.2). Ці самі рівняння задовільняє й електричне поле у вакуумі.

Рівняння (2.1) і (2.2), що описують поля у провідному середовищі й вакуумі, мають розв’язки, залежні від граничних умов. Розглянемо граничні умови на електродах та інших поверхнях розділу середовищ. Якщо електропровідність середовища мала, то малий і струм, який протікає через це середовище. Електропровідність електродів, з іншого боку, велика, тому можна знехтувати падінням напруги в їх об’ємі та вважати, що поверхні електродів є еквіпотенціальними. Тому лінії струму й силові лінії у малопровідному середовищі перпендикулярні до межі розділу електрод – малопровідне середовище.

Аналогічний хід силових ліній в діелектричному середовищі, наприклад, у вакуумі. Проте граничні умови повинні виконуватися не тільки на поверхні розділу електрод – середовище, але й на інших поверхнях, що його обмежують.

Як малопровідне середовище використовується електропровідний папір, а межують з ним повітря та ізолююча підкладка. Оскільки на межах між електропровідним папером. Повітрям і підкладкою електричний струм не може проходити перпендикулярно до поверхні розділу (з непровідного середовища у провідне), то в провідному середовищі встановлюється такий розподіл потенціалу, за якого вектор Е не матиме складових, перпендикулярних до поверхні розділу. Тому в провідному середовищі лінії струму й силові лінії йдуть вздовж межі розділу з непровідним середовищем. Межа розділу не вносить викривлень у форму ліній струму і, отже, ліній напруженості, якщо контур цієї межі відповідає контуру ліній струму.

У разі виконання всіх цих умов можна створити модель поля електростатичних зарядів, використовуючи поле в малопровідному середовищі. У такому моделюванні силовим лініям електростатичного поля відповідають лінії струму, а поверхням однакового потенціалу – поверхні однакових напруг. Перевагою такого моделювання є те, що виміряти поля у провідному середовищі набагато простіше, ніж у непровідному. Ця простота зумовлена тим, що в провідному середовищі вимірюється електричний потенціал, замість напруженості поля. Для таких вимірювань використовують зонди (електроди), які вводять у поле.

Зонд – це добре ізольований вздовж усієї довжини, крім кінця, провідник. Для вимірювання різниці потенціалів між двома точками поля в провідному середовищі потрібно доторкнутися до цих точок зондами, під’єднаними до вольтметра. Таким методом на електропровідному папері можна намітити лінії однакового потенціалу які відповідають лініям напруженості електростатичного поля всередині циліндричного конденсатора. Такий самий характер має розподіл потенціалу електростатичного поля безмежної, рівномірно зарядженої нитки.

Поле моделюється за допомогою електропровідного паперу, до якого щільно притиснуті два коаксіальних циліндричних електроди. Для такої моделі залежність напруженості, потенціалу поля від відстані r до осі системи та густину струму j(r) знаходимо з умови неперервності

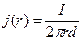де І – повний струм, що проходить через папір; d – товщина паперу.

Тоді напруженість поля на відстані r

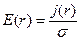, або ,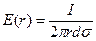

де σ - електрична провідність паперу.

Експериментальна установка може бути зібрана так, щоб в досліді вимірювалася різниця потенціалів між зовнішнім електродом, потенціал якого приймається таким, що дорівнює нулю, і даною точкою поля. Розрахуємо теоретично цю різницю потенціалів, використавши зв’язок між напруженістю поля та його потенціалом:

E = - gradφ.

У полярній системі координат ця рівність перепишеться так:

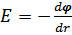Звідки, врахувавши,що U(r)= φ(r)- φ(r_з) та φ(r_з)=0, маємо

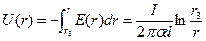де r₃ – радіус зовнішнього електрода.

Одержані вирази для U(r) і Е(r) можна переписати у вигляді, зручному для дослідження, якщо замість σ, I, d ввести величини r₃, r_вн, U₀,,що легко вимірюються експериментально (r_вн – радіус внутрішнього електрода, U₀ – різниця потенціалів між зовнішнім і внутрішнім електродами):

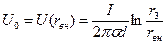; (2.3)

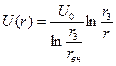; (2.4)

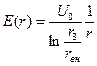. (2.5)

Зміст даної роботи полягає у визначенні залежностей U = U(r) і Е = Е(r) дослідним шляхом та порівнянні отриманих результатів з залежностями, отриманими теоретично за формулами (2.4) і (2.5)).

<== попередня сторінка	\|	наступна сторінка ==>
	\|	Опис експериментальної установки

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.041 сек.