• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Визначення методу ДП

Синтез оптимальних систем на основі динамічного програмування (ДІ1)

Визначення методу ДП

Динамічне програмування являє собою математичний метод оптимізації систем, функціонування яких представляє певну низку багатокрокових операцій (навпаки, ЛП призначено для пошуку оптимуму саме однокрокових операцій).

Уявимо собі, що досліджувані операції являють собою процес, що розвивається в часі і який розділяється на ряд «кроків». Наприклад, економічна діяльність підприємства (Q) протягом ряду років планується й оптимізується на кожний рік, що є природним кроком розвитку підприємства. Природно, що керування діяльністю підприємства буде складатися з елементарних «крокових» управлінь, сукупність яких називається стратегією управління.

Нехай на початку періоду, що розглядається, на розвиток системи підприємств, які виконують певні функції виробництва одного виду продукції, виділені деякі кошти Kq. Ці кошти повинні бути розподілені між підприємствами. У процесі функціонування ці кошти частково витратяться (тобто амортизуються). Крім того, кожне підприємство приносить доход, що залежить від вкладених коштів. На початку кожного наступного року наявні кошти, що залишилися, можуть знову якось розподіляться між підприємствами.

Постає питання: як потрібно розподіляти кошти між підприємствами на протязі кожного року, щоб сумарний доход від усіх систем підприємств на період Т, був максимальним. Саме це є типовою задачею ДП. Перерозподіл коштів на початок кожного року і представляє поточний крок управління.

Нехай на початку і'-го року підприємствам 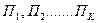виділені відповідні кошти:

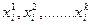(к - му підприємству в і - й рік).

Сукупність цих значень являє собою не що інше, як крокове управління на /-му кроці: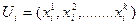

Керування ж системою підприємств за період Т, що містить m кроків (років) являє собою сукупність

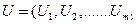і являє собою стратегію управління.

Ефективність цієї стратегії на і-му кроці визначається показником ефективності (наприклад, отриманим доходом):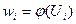

Тоді за весь період Т ( за т - кроків) показник ефективності визначається як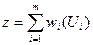

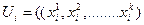Згідно з типовою задачею ДП необхідно вибрати стратегію управління усіма к підприємствами на і - му кроці:

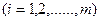
що забезпечує і = z_nm.

Поставлену задачу можна вирішити по різному:

- відразу знайти оптимальне рішення и (для оптимальної стратегії
приймемо ії позначку маленькою буквою и);

- на кожнім і-му кроці будемо оптимізувати тільки відповідне
управління и_і, у результаті такого розгляду за т кроків буде
знайдена оптимальна стратегія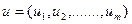

при якій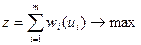

Здавалося б рішення тривіальне: необхідно оптимізувати крокові управління и_і, щороку (це просто, із застосуванням ЛП) і в результаті оптимізації всіх кроків одержимо оптимальну стратегію управління и.

Але принцип ДП аж ніяк не припускає, що кожен крок оптимізується окремо, незалежно від інших. Навпаки, крокове управління повинне вибиратися з урахуванням усіх його наслідків у майбутньому. Цей принцип сформульований американським вченим Робертом Беллманом, говорить, що незалежно від того, який стан системи і яке прийняте рішення в початковий момент, наступні рішення і отже поводження системи має бути оптимальним з урахуванням саме майбутніх наслідків.

Однак з цього загального правила є одне єдине виключення: останній крок, який може просто плануватися як оптимальний у рамках ЛП (без урахування наслідків), і який має приносити безумовно максимальну вигоду.

Таким чином, спланувавши цей останній крок, можна до нього пристроювати передостанній, потім предпередостанній і т.д. до початкового кроку.

Саме тому процес ДП розвертається, як правило, від кінця до початку. Але як же це спланувати, не знаючи передостаннього? Очевидно, потрібно зробити певні припущення щодо результатів передостаннього (т-1)-го кроку і для нього знайти таке управління, що забезпечить максимальний виграш на останньому m-му кроці.

Нехай це процедура виконання для кожного з можливих станів системи на (т-1) кроці і для кожного з них ми знаємо оптимальне керування на m-му кроці. Тепер ми можемо оптимізувати керування на (т-1) кроці, зробивши всі можливі припущення щодо стану системи на (т -2)-у кроці. Для кожного з цих припущень знаходимо оптимальний вектор управління и _т-1

Іншими словами, на кожнім і-у кроці шукається управління и яке забезпечує оптимальне продовження процесу на (і+1) - кроці відносно досягнутого стану на і-му кроці.

Управління, що забезпечує оптимальне продовження процесу називається умовним оптимальним управліннямна даному кроці (УОУ).

Тепер припустимо, що УОУ на кожному кроці нам відомо: ми знаємо як йти далі, у якому би стані не був процес до початку кожного кроку. Тоді, якщо початковий стан So нам відомий, то ми знаємо, як знайти вже не умовне, а дійсно оптимальне управління на 1-му кроці. Потім, спираючись на нього, можна знайти оптимальне управління на другому кроці і т.д. У результаті ми прийдемо до кінцевого стану S_m і знайдемо оптимальний вектор управління и, що забезпечить оптимальне протікання процесу протягом усіх т кроків управління.

Таким чином, при оптимізації систем методом ДП багатокроковий процес проходить двічі:

- від кінцевого кроку до початкового, при цьому знаходяться
оптимальні умовні управління;

- від початкового кроку до кінцевого, при цьому знаходяться серед
множини умовних оптимальних управлінь уже реальні
оптимальні управління на кожному кроці з урахуванням
результатів попереднього кроку (як початкові умови наступного).

Розглянемо декілька прикладів застосування методу ДП.

7.2 Знаходження найкоротшої відстаніміж двома вузлами на мережі доріг

Це одна з перших транспортних задач, що були вирішені методом ДП.[12].

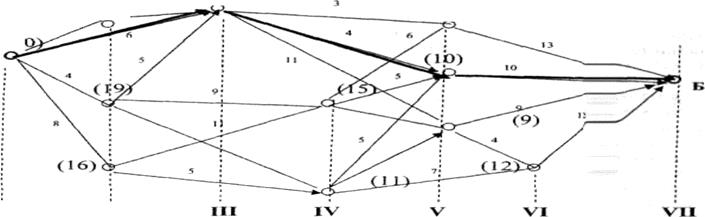
Рис.7.1 До визначення найкоротшого шляху

Нехай відома мережа автомобільних доріг, яка з'єднує пункти А і В. Ця мережа складається із сукупності вузлів і з'єднуючих їх доріг. Поставимо задачу пошуку найкоротшого шляху між пунктами А і Б (див. рис.7.1).

Рухаючись від останнього кроку до першого (від Б до А), знайдемо умовно оптимальне рішення на кожному кроці.

VI-й крок. На цьому кроці є одна умовна точка. Припустімо, що ми вже потрапили в цю точку (незалежно як) і будемо намагатися потрапити в кінцеву точку Б. Є тільки один шлях , тому це і буде найкоротша відстань =12 (оцінку цієї вузлової крапки змінимо 12).

V - крок. На цьому кроці маємо 3 точки. Якщо ми потрапили (незалежно як) у верхню крапку , то найкоротша відстань до Б буде дорівнює 13, для другої точки 10, для третьої - 9, покажемо стрілками напрямок руху в крапку В.

IV — крок. На цьому кроці маємо дві крапки. З верхньої крапки виходить три напрямки. Необхідно вибрати оптимальний напрямок. Якщо рухатися в напрямку крапки 13, то відстань до крапки Б , буде 6 +(13) = 19.

Якщо рухатися в напрямку крапки з оцінкою (10), тс відстань до Б буде дорівнює 5 + (10) = 15; а якщо в напрямку крапки з оцінкою (9), то 8+(9)=17. нас цікавить напрямок який дасть мінімальну оцінку, тому мінимо оцінку цієї крапки, рівної мінімальній з перелічених (15). Аналогічно знаходимо оцінку для другої крапки кроку IV 6+(10)=16; 2+(9)=11;7+(12)=13.

Мінімальне значення в напрямку крапки (9) далі буде дорівнює (11). Оптимальні значення позначимо стрілками.

III - крок. На цьому кроці одна вузлова точка з якої виходить три напрямки 3+(13)=16;4+(10)=14; П+(9)=20.

Мінімальну оцінку (14) одержимо рухаючи у вузлову крапку з оцінкою (10).

ІІ- крок. На цьому кроці 3 вузлові точки : Для верхньої: 7+(14)=21;

Для другої : 5+(14)=19; 9+(15)=24; 10+(11)=21. мінімальна оцінка (19) у напрямку крапки з оцінкою (14; Для третьої : 4+(15)=19; 5+(11)=16.

Умовно - оптимальної є оцінка (13) і умовно - оптимальним управлінням - рух у кутову крапку з оцінкою (11).

І - крок містить 4 можливі напрямки: 3+(21)=24; 6+(14)=20; 4+(19)=23; 8+(16)=24. Мінімальна сума (20) у напрямку крапки з оцінкою (14).

Таким чином, оцінка (20) для початкової точки є найкоротшою відстанню між А і Б. Для вибору оптимального управління (вибору найкоротшого напрямку руху) необхідно знайти такий шлях від А до Б, на якому не перериваються стрілки. Таким шляхом буде

А -> (13) -» (10) -> В.

Варто мати на увазі, що потрапивши в будь-яку точку, ми завжди знайдемо найкоротший маршрут у Б. Наприклад, із точки (16) таким маршрутом буде: (16) -> (11) ~> (9) -»Б, з відстанню, яка дорівнює 11 + 15=26.

Відзначимо, що цей алгоритм обчислення найкоротшої відстані зветься алгоритмом дослідження всіх можливих шляхів або алгоритмом Кука і Холсея (по імені його авторів)

Переглядів: 349