
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Інтервали монотонності та точки екстремуму функцій.
Будь-яке дослідження функції треба розпочинати з знаходження області її визначення. Обсяг досліджень можна зменшити, якщо функція парна чи непарна, або періодічна. Щоб не робити зайвої роботи, після знаходження області визначення доцільно провести дослідження функції на парність та періодичність.
Функція 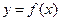 може бути парною або непарною лише у тому випадку, коли її область визначення симетрична відносно нуля Якщо ця умова не виконана, то вона ні парна, ні непарна, або, як часто кажуть, загального вигляду.
може бути парною або непарною лише у тому випадку, коли її область визначення симетрична відносно нуля Якщо ця умова не виконана, то вона ні парна, ні непарна, або, як часто кажуть, загального вигляду.
Функція 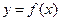 з симетричною відносно нуля областю визначення парна, якщо
з симетричною відносно нуля областю визначення парна, якщо 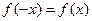 , і непарна, якщо
, і непарна, якщо 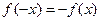 для всіх
для всіх 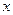 з її області визначення.
з її області визначення.
Приклад 4.1. Дослідити на парність функцію
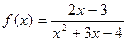 .
.
Розв’язок. Визначимо облать визначення функції. Вона, очевидно, визначається нерівністю 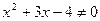 (чому?). Її розв’язок
(чому?). Її розв’язок 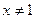 ,
, 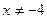 . Отже, область визначення функції
. Отже, область визначення функції 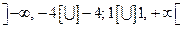 (Рис. 4.1).
(Рис. 4.1).
Через те, що область визначення не є симетричною відносно нуля, функція ні парна, ні непарна, тобто загального вигляду.

Приклад 4.2. Дослідити на парність функцію
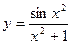 .
.
Розв’язок. Область визначення цієї функції 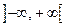 (чому?) симетрична відносно нуля. Отже, функція може бути парною або непарною.
(чому?) симетрична відносно нуля. Отже, функція може бути парною або непарною.
Оскільки
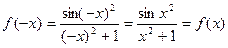 ,
,
то функція є парною.
Графік парної функції симетричний відносно осі ординат, а графік непарної функції симетричний відносно початку координат. Отже, як парну, так і непарну функцію достатньо дослідити лише на половині області визначення: для 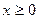 або для
або для 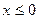 .
.
Інтервали монотонності та точки екстремуму доцільно шукати одночасно. Порядок находження інтервалів монотонності і екстремумів функції може бути таким:
1) знайти область визначення функції;
2) дослідити функцію на парність. Якщо функція парна або непарна, то подальше дослідження можна робити лише на половині області визначення функції, наприклад, при 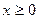 ;
;
3) дослідити функцію на періодичність. Якщо функція періодична, то подальше дослідження можна робити на проміжку довжиною один період, а якщо функція при цьому ще й парна або непарна, то подальше дослідження можна робити на половині періоду;
4) знайти критичні точки функції, тобто точки області визначення функції, у яких її похідна дорівнює нулю або не існує. Ці точки розіб’ють область визначення на інтервали, у яких похідна зберігає знак;
5) визначити знак похідної у кожному з одержаних інтервалів. Для цього досить обчислити (або хоча б визначити знак) значення похідної у довільній точці кожного інтервалу;
6) у інтервалах, де похідна додатна, функція зростає, у інтервалах, де похідна від’ємна, функція спадає. У критичних точках, у яких функція неперервна і при переході через які зліва направо похідна змінює знак з плюса на мінус, функція має масимум, а у критичних точках, у яких функція неперервна і при переході через які зліва направо похідна змінює знак з мінуса на плюс, функція має мінімум. Якщо при переході через критичну точку похідна неперервної функції не змінює знак, то у цій точці функція не має екстрему;
7) обчислити екстремальні значення функції, тобто значення функції у точках екстремуму.
Результати досліджень зручно ілюструвати на осі абцис, як це зроблено у наведеному нижче прикладі.
Приклад 4.3. Знайти інтервали монотонності та точки екстремуму функції
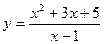 .
.
Розв’язок. Область визначення функції 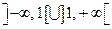 (чому?) (рис.4.2.).
(чому?) (рис.4.2.).
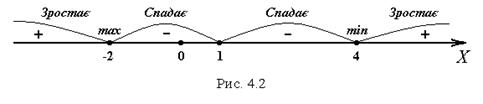
Область визначення не є симетричною відносно нуля, отже, функція загального вигляду, і неперіодична як алгебраїчна функція.
Знайдемо критичні точки функції:
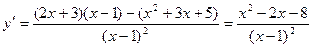 .
.
Похідна дорівнює нулю, якщо
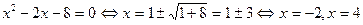 .
.
Похідна не існує при 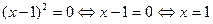 , однак ця точка не належить до області визначення функції, тобто не є її критичною точкою.
, однак ця точка не належить до області визначення функції, тобто не є її критичною точкою.
Отже, функція має дві критичні точки: 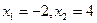 .
.
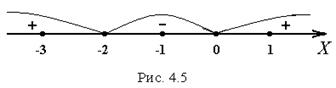
Критичні точки розбивають область визначення функції на чотири інтервали: 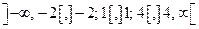 (рис.4.2).
(рис.4.2).
Визначимо знак похідної у кожному з інтервалів, для чого обчислимо значення похідної у точках 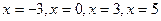 , кожна з яких є внутрішньою точкою для одного з інтервалів:
, кожна з яких є внутрішньою точкою для одного з інтервалів:
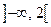
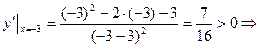 - функція зростає,
- функція зростає,
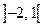
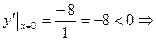 - функція спадає,
- функція спадає,
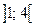
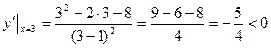 - функція спадає,
- функція спадає,
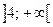
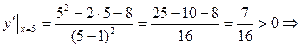 - функція зростає.
- функція зростає.
Таким чином, у інтервалах 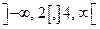 функція зростає, а у інтерваліах
функція зростає, а у інтерваліах 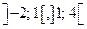 - спадає. У критичній точці
- спадає. У критичній точці 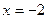 функція має максимум (чому?), а у критичній точці
функція має максимум (чому?), а у критичній точці 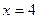 - мінімум (чому?).
- мінімум (чому?).
Обчислимо екстремальні значення функції:
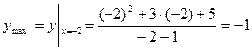 ;
;
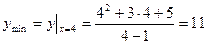 .
.
Питання для самоперевірки.
1. З чого слід почати будь-які дослідження функції?
2. Дайте означення парної та непарної функції.
3. Дайте означення періодичної функції. Що називається періодом та основним періодом функції?
4. Наведіть приклади функції, які є одночасно парними та непарними, та функції, які мають безліч основних періодів.
5. Які спрощення у дослідженнях можливі, якщо функція парна, непарна, або періодична?
6. Дайте означення функції, зростаючої, спадаючої та монотонної на інтервалі?
7. Дайте означення точки максимуму, точки мінімуму та точки екстремуму функції.
8. Сформулюйте й виведіть необхідну й достатню умови зростання (спадання) функції у інтервалі.
9. Які точки називаються критичними точками функції?
10. Сформулюйте необхідну умову існування екстремуму функції у точці.
11. Сформулюйте достатні умови існування екстремуму функції за допомогою першої похідної.
12. Сформулюйте достатню умову існування екстремуму функції за допомогою другої похідної.
13. У якому порядку визначаються інтервали монотонності та точки екстремуму функції?
Л і т е р а т у р а: [3, № 20; 4, гл. 5, № 4. 4-4. 12; 5, гл. 4, § 4.17 або 6, гл. 5, § 1-5].
4.2. Найбільше та найменше значення функції на відрізку.
Для функцій неперервних у замкненому проміжку має місце теорема Вейєрштраса: якщо функція 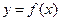 неперервна на відрізку
неперервна на відрізку 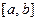 , то вона досягає на ньому найбільшого значення
, то вона досягає на ньому найбільшого значення 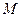 і найменшого значення
і найменшого значення 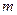 . Інакше кажучи, на відрізку
. Інакше кажучи, на відрізку 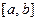 знайдуться такі точки
знайдуться такі точки 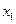 і
і 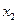 , що значення
, що значення 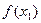 і
і 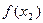 будуть відповідно найбільшими і найменшими з усіх значень функції
будуть відповідно найбільшими і найменшими з усіх значень функції 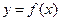 на цьому відрізку.
на цьому відрізку.
Для знаходження найбільшого та найменшого значень функції на відрізку достатньо знайти критичні точки, що йому належать, обчислити значення функції у цих критичних точках та на кінцях відрізка і з усіх отриманих значень функції вибрати найбільше і найменше. Це й буде найбільше і найменше значення функції на даному відрізку.
Зверніть увагу! У прикладних задачах часто зустрічається такий випадок, коли всередині заданого проміжку (відрізку або інтервалу) є лише одна критична точка. Якщо у цій точці функція має максимум (або мінімум), то без порівняння з її значеннями на кінцях проміжутку зрозуміло, що у цій точці й буде найбільше (або найменше) значення функції на заданому відрізку. Слід відзначити, що це є справедливим також і для нескінченного проміжку.
Приклад 4.4. Обчислити найбільше і найменше значення на відрізку 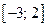 функції
функції
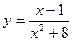 .
.
Розв’язок. Задана функція неперервна на відрізку 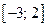 , отже, приймає найбільше та найменше значення на цьому відрізку. Для їх обчислення знайдемо спочатку критичні точки, що лежать у середині відрізку
, отже, приймає найбільше та найменше значення на цьому відрізку. Для їх обчислення знайдемо спочатку критичні точки, що лежать у середині відрізку 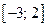 , тобто точки, у яких похідна дорівнює нулю або не існує:
, тобто точки, у яких похідна дорівнює нулю або не існує:
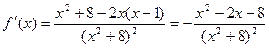 .
.
Звідси маємо 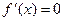 , якщо
, якщо 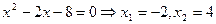 .
.
Точка 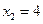 не входить до відрізка
не входить до відрізка 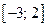 .
.
Обчислимо значення функції у знайденій критичній точці і на кінцях відрізка 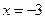 ,
, 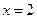 .
.
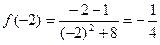 ;
; 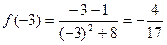 ;
; 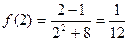 .
.
З усіх отриманих значень функції оберемо найбільше та найменше. Таким чином 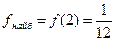 ;
;  , тобто задана функція найбільше значення приймає на правому кінці відрізка, а найменше - усередині відрізка.
, тобто задана функція найбільше значення приймає на правому кінці відрізка, а найменше - усередині відрізка.
Приклад 4.5. Текст, надрукований на сторінці книги, повинен займати 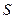 см. Поля зверху і знизу повинні бути по
см. Поля зверху і знизу повинні бути по 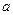 см, а справа й зліва - по
см, а справа й зліва - по 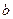 см. Обчислити найбільш економні розміри паперу.
см. Обчислити найбільш економні розміри паперу.
Розв’язок. Складемо спочатку функцію, найбільше або найменше значення якої треба буде шукати. Нехай аркуш паперу має форму прямокутника 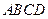 , а друкований текст займає площу прямокутника
, а друкований текст займає площу прямокутника 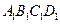 . Позначимо довжину сторін прямокутника відповідно
. Позначимо довжину сторін прямокутника відповідно 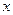 і
і 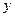 . Очевидно, що найбільш економні розміри аркуша паперу ті, за яких його площа буде найменшою (при заданій площі тексту). Позначимо її літерою
. Очевидно, що найбільш економні розміри аркуша паперу ті, за яких його площа буде найменшою (при заданій площі тексту). Позначимо її літерою 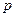 :
: 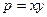 . Одержимо функцію двох змінних
. Одержимо функцію двох змінних 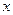 і
і 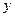 . Одну змінну виключаємо, використовуючи, що площа прямокутника
. Одну змінну виключаємо, використовуючи, що площа прямокутника 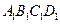 задана і дорівнює
задана і дорівнює 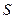 :
: 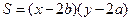 .
.
Звідси
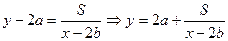 ,
,
звідки 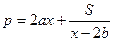 ,
, 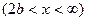 .
.
Таким чином, необхідно знайти найменше значення функції 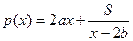 на інтервалі
на інтервалі 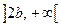 .
.
Знаходимо критичні точки, що лежать на цьому інтервалі:
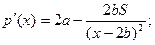
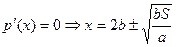 .
.
Інтервалові 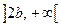 належить тільки значення
належить тільки значення 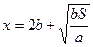 .
.
Для того, щоб визначити, чи є у знайденій критичній точці 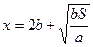 екстремум, скористуємось другою достатньою умовою існування екстремуму. Якщо
екстремум, скористуємось другою достатньою умовою існування екстремуму. Якщо 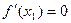 і
і 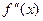 існує і неперервна в деякому околі точки
існує і неперервна в деякому околі точки 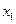 , то при
, то при 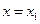 функція
функція 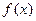 має максимум, якщо
має максимум, якщо 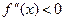 , та мінімум, якщо
, та мінімум, якщо 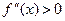 .
.
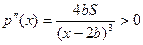 ,
, 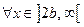 .
.
Отже, при 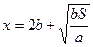 функція
функція 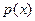 має мінімум. Оскільки це єдина точка екстремуму неперервної на інтервалі функції, то в ній вона має найменше значення. Відповідне значення
має мінімум. Оскільки це єдина точка екстремуму неперервної на інтервалі функції, то в ній вона має найменше значення. Відповідне значення 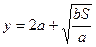 .
.
Таким чином, найбільш економні розміри паперу
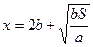 ,
, 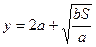 .
.
Питання для самоперевірки.
1. Що називається найбільшим значенням функції на відрізку?
2. Що називається найменшим значенням функції на відрізку?
3. Як знайти найбільше й найменше значення неперервних функцій на заданому відрізку?
4. Чи може функція, що має максимум (мінімум), не мати найбільшого (найменшого) значення? Наведіть приклади.
5. Чи може функція, що має найбільше (найменше) значення, не мати максимум (мінімум)? Наведіть приклади.
14. У якому порядку визначаються інтервали монотонності та точки екстремуму функції?
Л і т е р а т у р а: [3, № 121; 4, гл. 5, № 4.13–4.20, 4.25–4.39; 5, гл. 4, § 4.18 або 6, гл. 5, § 6].
4.3. Інтервали опуклості догори, опуклості донизу і точки перегину графіка функції.
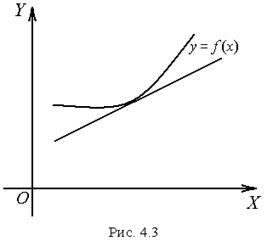
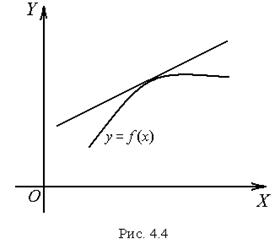
Треба звернути увагу, що поняття опуклості функції пов’язані з опуклістю її графіка. Кожний інтуітивно може уявити собі опуклу поверхню (наприклад зовнішня поверхня сфери). Будь-яка плоска крива на такій поверхні є опуклою. Протилежним до опуклості поняттям є поняття угнутості. Графік тієї ж самої функції є опуклим чи увігнутим залежно від того, звідки дивитись: знизу чи згори (рис. 4.3). Тому краще говорити про опуклість донизу (рис. 4.3) і опуклість догори функції (рис.4.4). Значення напрямку опуклості функції пов’язують з розташуванням її графіка відносно дотичних до графіка. Функція  вважається опуклою донизу у деякому інтервалі, якщо усі точки іі графіка у цьому інтервалі розташовані нижче дотичної, проведеної у будь-якій точці графіка, і випуклою догори, якщо усі точки її графіка у цьому інтервалі розташовані не вище дотичної, проведеної у будь-якій точці графіка.
вважається опуклою донизу у деякому інтервалі, якщо усі точки іі графіка у цьому інтервалі розташовані нижче дотичної, проведеної у будь-якій точці графіка, і випуклою догори, якщо усі точки її графіка у цьому інтервалі розташовані не вище дотичної, проведеної у будь-якій точці графіка.
Функція може бути опукла догори у одних інтервалах її області визначення і опукла донизу у інших. Точки графіка функції, у яких змінюється напрямок опуклості, носять назву точок перегину. Слід мати на увазі, що напрямок опуклості може змінитися не лише у точках перегину, але й у точках розриву функції.
Порядок знаходження інтервалів опуклості догори, опуклості донизу та точок перегину є аналогічним до порядку знаходження інтервалів монотонності і екстремумів функції, тільки замість першої розглядається друга похідна функції. Він може бути таким:
1) знайти область визначення функції;
2) дослідити функцію на парність;
3) дослідити функцію на періодичність;
4) знайти критичні точки другого роду функції, тобто точки, у яких її друга похідна дорівнює нулю або не існує. Ці точки розіб’ють область визначення функції на інтервали, у яких друга похідна зберігає знак;
5) визначити знак другої похідної у кожному з отриманих інтервалів. Для цього досить обчислити (або хоча б визначити знак) значення другої похідної у одній з внутрішніх точок кожного інтервала;
6) у інтервалах, де друга похідна додатна, функція опукла донизу, у інтервалах, де друга похідна від’ємна, функція опукла догори. Критичні точки другого роду, що належать області визначення функції, при переході через які змінює знак, є точки перегину функції;
7) обчислити значення функції у точках перегину.
Результати досліджень зручно ілюстровати на осі абцис, як це зроблено у наведеному нижче прикладі.
Приклад 4.6. Знайти інтервали опуклості догори, опуклості донизу і точки перегину функції
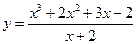 .
.
Розв’язок. Область визначення функції 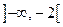 È
È 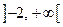 . Функція загального виду (чому?), неперіодична. Відшукуємо критичні точки другого роду функції
. Функція загального виду (чому?), неперіодична. Відшукуємо критичні точки другого роду функції
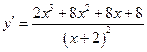 ,
, 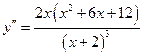 .
.
Перевірте!
Друга похідна дорівнює нулю при 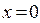 і не існує при
і не існує при 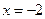 , але ця точка не належить області визначення заданої функції (точка розриву). Отже, функція має одну критичну точку другого роду:
, але ця точка не належить області визначення заданої функції (точка розриву). Отже, функція має одну критичну точку другого роду: 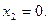
Критична точка та точка розриву функції, поділили область визначення функції на три інтервали 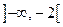 ,
, 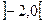 ,
, 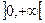 .
.
Визначимо знак другої похідної функції у кожному інтервалі:
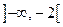
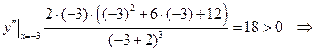 функція опукла донизу,
функція опукла донизу,
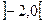
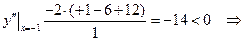 функція опукла догори,
функція опукла догори,
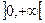
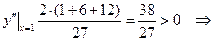 функція опукла донизу.
функція опукла донизу.
Точка з абсцисою 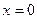 є точкою перегину функції.
є точкою перегину функції.
Ордината точки перегину 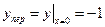 .
.
Відмітимо, що напрямок опуклості функції змінюється також у точці 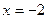 , що є точкою розриву функції.
, що є точкою розриву функції.
Питання для самоперевірки.
1. У якому разі функція 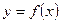 називається опуклою донизу (догори) у деякому інтервалі?
називається опуклою донизу (догори) у деякому інтервалі?
2. Що таке точки перегину функції?
3. Сформулюйте і поясніть необхідну і достатню умови опуклості догори (донизу) функції у інтервалі?
4. Яким є порядок знаходження інтервалів опуклості донизу, опуклості догори та точок перегину функції?
Л і т е р а т у р а: [3, № 124; 4, гл. 5, № 4.40-4.51; 5, гл. 4, § 4.79 або 6, гл. 5, § 9].
4.4. Асимптоти графіка функції.
Асимптоти дозволяють створити уявлення про вид графіка функції при віддаленні його точок на нескінченність. Саме це визначає їхню роль при вивченні поведінки функції. Вертикальні асимптоти - це прямі 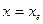 , де
, де 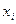 - точки розриву другого роду, при наближенні до яких функція необмежено зростає за модулем.
- точки розриву другого роду, при наближенні до яких функція необмежено зростає за модулем.
Горизонтальні асимптоти можна не шукати окремо, бо вони є частинним випадком похилих асимптот 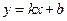 при
при 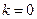 ; якщо область визначення функції не обмежена в обидва боки, то при находженні похилих асимптот слід окремо розглядати випадки
; якщо область визначення функції не обмежена в обидва боки, то при находженні похилих асимптот слід окремо розглядати випадки 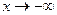 та
та 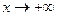 , тому що можуть бути дві різні асимптоти.
, тому що можуть бути дві різні асимптоти.
Приклад 4.7. Знайти асимптоти графіка функції
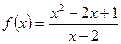 .
.
Розв’язок. Область визначення функції 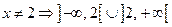 . Точка
. Точка 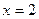 єдина точка розриву функції. Дослідимо її:
єдина точка розриву функції. Дослідимо її:
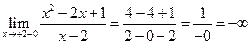 ,
,
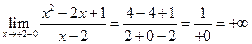 .
.
Через те, що при 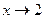 функція необмежено зростає за модулем, пряма
функція необмежено зростає за модулем, пряма 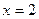 - вертикальна асимптота функції.
- вертикальна асимптота функції.
Знайдемо похилі (невертикальні) асимптоти функції, якщо вони є. Рівняння таких асимптот мають вигляд 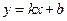 , де
, де
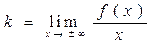 ,
, 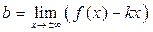 .
.
Знайдемо 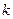 та
та 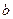 для нашої функції:
для нашої функції:
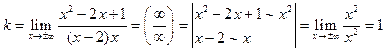 ,
,
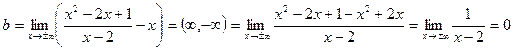 .
.
Таким чином, дана функція має одну й ту саму похилу асимптоту 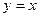 і при
і при 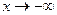 , і при
, і при 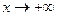 .
.
Приклад 4.8. Знайти асимптоти функції 
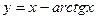 .
.
Розв’язок. Область визначення функції: 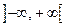 .
.
Точок розриву немає. Отже, немає й вертикальних асимптот.
Знайдемо невертикальні асимптоти функції, якщо вони є. Їхнє рівняння має вигляд 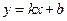 , де
, де
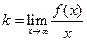 ,
, 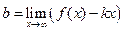 ,
,
Знайдемо 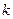 і
і 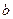 для нашої функції:
для нашої функції:
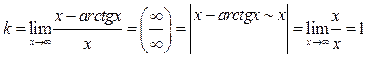
(і при  , і при
, і при  ).
).
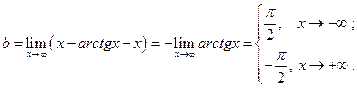 .
.
Таким чином, функція має дві похилі асимптоти: 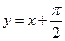 при
при 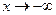 і
і 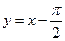 при
при 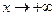 .
.
Питання для самоперевірки.
1. Якою є роль асимптоти при дослідженні функції та її графіка?
2. Що називається асимптотою графіка функції?
3. Як знаходять вертикальні асимптоти?
4. Як знаходять похилі та горизонтальні асимптоти?
Л і т е р а т у р а: [3, № 125; 4, гл. 5, № 4.52-4.60; 5, гл. 4, № 4.20 або 6, гл.5, № 10].
4.5. Загальна схема дослідження функції та побудови її графіка.
Повне дослідження функції та побудову її графіка можна робити у такій послідовності:
1. знайти область визначення функції (розд. 3.1);
2. дослідити функцію на парність (розд. 4.1);
3. дослідити функцію на періодичність (розд. 4.1);
4. дослідити точки розривів функції й відшукати та побудувати вертикальні асимптоти, якщо вони є (розд. 4.4);
5. знайти і побудувати невертикальні асимптоти, якщо вони є (розд. 4.4);
6. знайти інтервали монотонності й екстремуми функції (розд. 4.1), побудувати точки екстремумів;
7. знайти інтервали опуклості догори, опуклості донизу і точки перегину функції (розд. 4.3), побудувати точки перегину;
8. за знайденими “опорними” точками побудувати графік функції, враховуючи з’ясовану поведінку функції між “опорними” точками.
До “опорних” точок можна приєднати й інші. Часто до них приєднують точки перетину графіка з координатними осями. Проте точки перетину з віссю 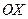 не завжди можуть бути знайдені. Часто графік будують саме для того, щоб хоча б наближено віднайти ці точки.
не завжди можуть бути знайдені. Часто графік будують саме для того, щоб хоча б наближено віднайти ці точки.
Приклад 4.9. Дослідити функцію

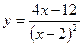
і побудувати її графік.
Розв’язок. Область визначення функції: 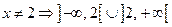 .
.

Через те що область визначення функції не є симетричною відносно початку координат, функція ні парна, ні непарна; функція неперіодична.
Дослідимо точку розриву 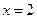 у якій можлива вертикальна асимптота графіка функції.
у якій можлива вертикальна асимптота графіка функції.
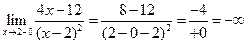 ,
, 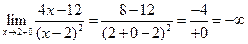
Ліва та права границі функції у точці 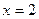 дорівнюють нескінченності, тому точка
дорівнюють нескінченності, тому точка 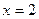 є точкою розриву другого роду. Оскільки функція необмежено спадає при
є точкою розриву другого роду. Оскільки функція необмежено спадає при 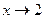 , то пряма
, то пряма 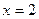 - вертикальна асимптота графіка функції. Побудуємо її на рисунку (див. рис.4.9).
- вертикальна асимптота графіка функції. Побудуємо її на рисунку (див. рис.4.9).
Знайдемо невертикальні асимптоти 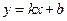 .
.
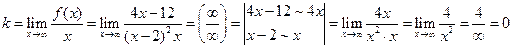 ,
,
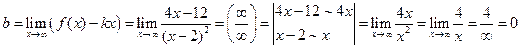
Отже, пряма 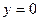 (вісь
(вісь 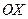 ) - горизонтальна асимптота графіка функції. Побудуємо її на рисунку ( див. рис.4.9).
) - горизонтальна асимптота графіка функції. Побудуємо її на рисунку ( див. рис.4.9).
Знайдемо інтервали монотонності й екстремуми функції. Результати досліджень наведені на рис. 4.7.
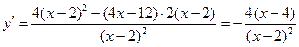 .
.
Похідна дорівнює нулю при 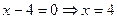 і не існує при
і не існує при 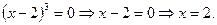
Таким чином, точка розриву 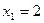 та критична точка
та критична точка 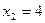 ділять область визначення функції на три інтервали:
ділять область визначення функції на три інтервали: 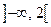 ,
, 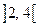 ,
, 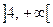 .
.
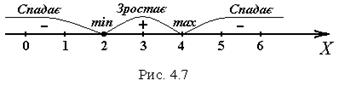
Визначимо знак похідної у кожному інтервалі:
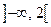
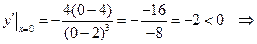 функція спадає,
функція спадає,
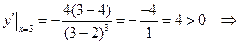 функція зростає,
функція зростає,
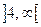
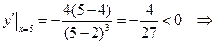 функція спадає.
функція спадає.
У точці 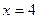 функція має максимум, тому що при переході через цю точку похідна змінює знак з плюса на мінус.
функція має максимум, тому що при переході через цю точку похідна змінює знак з плюса на мінус.
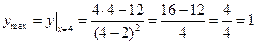 .
.
Зазначимо, що хоч у точці 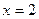 похідна змінює знак з мінуса на плюс, проте мінімуму функція у цій точці не має, бо це точка розриву (
похідна змінює знак з мінуса на плюс, проте мінімуму функція у цій точці не має, бо це точка розриву ( 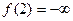 ). Іноді у таких випадках кажуть, що функція має невласний мінімум у точці
). Іноді у таких випадках кажуть, що функція має невласний мінімум у точці 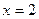 .
.
Знаходимо інтервали опуклості догори, опуклості донизу та точки перегину функції. Результати досліджень наведені на рис.4.8.
Знайдемо другу похідну:
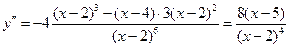 .
.
Друга похідна дорівнює нулю при 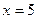 і не існує при
і не існує при 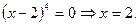
Таким чином, точка розриву 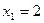 та критична точка другого роду
та критична точка другого роду 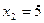 ділять область визначення на три інтервали:
ділять область визначення на три інтервали: 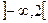 ,
, 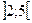 ,
, 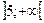 .
.
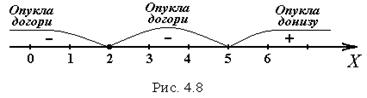
Визначимо знак другої похідної у кожному інтервалі:
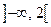
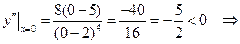 функція опукла догори,
функція опукла догори,
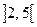
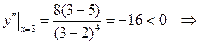 функція опукла догори,
функція опукла догори,
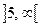
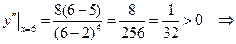 функція опукла донизу.
функція опукла донизу.
Через те що при переході через точку 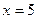 друга похідна змінює знак, точка з абсцисою
друга похідна змінює знак, точка з абсцисою 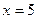 є точкою перегину функції.
є точкою перегину функції.
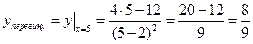 .
.
Побудуємо точку перегину 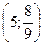 на рисунку (рис.4.9).
на рисунку (рис.4.9).
За отриманими “опорними” точками побудуємо графік.
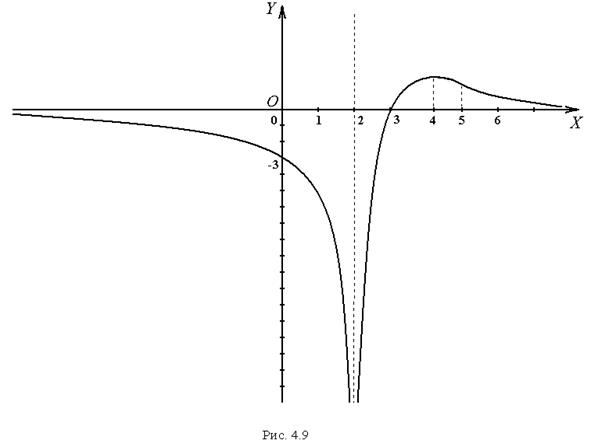
У цьому прикладі легко відшукати точки перетину графіка функції з координатними осями. З віссю 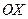 :
: 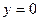 , якщо
, якщо 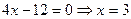 ; з віссю
; з віссю 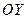 :
: 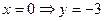 (див. рис.4.9).
(див. рис.4.9).
Питання для самоперевірки.
1. Яким є порядок дослідження функції та побудови її графіка?
2. Чи можна переставити пункти наведеного вище порядку дослідження функції і побудови її графік? Якщо можна, то як?
Л і т е р а т у р а: [3, № 126, 127; 4, гл. 5, 4.61-4.132; 5, гл. 4, 4.22 або 6, гл.5, № 11].
| <== попередня сторінка | | | наступна сторінка ==> |
| Додаток 2 | | | Пряма та двоїста задачі лінійного проґрамування |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |