
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Закон динаміки обертального руху матеріальної точки
Розглянемо обертальний рух матеріальної точки масою 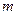 відносно точки О під дією сили
відносно точки О під дією сили 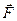 , яка в даний момент часу лежить в площині руху
, яка в даний момент часу лежить в площині руху
(рис.2). Складова сили 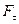 надає матеріальній точці
надає матеріальній точці  тангенціального прискорення, модуль якого
тангенціального прискорення, модуль якого 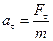 . Тоді
. Тоді 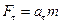 .
.
Дія нормальної складової сили 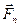 зводиться лише до надання точці
зводиться лише до надання точці 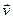 нормального приско-рення (закручування траєкторії). Оскільки за даних умов
нормального приско-рення (закручування траєкторії). Оскільки за даних умов 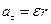 , то:
, то:
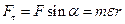
Домножимо вираз на 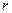 :
:
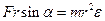 .
.
Увівши позначення 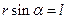 ,
, 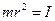 ,
, 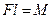 , запишемо останній вираз у вигляді:
, запишемо останній вираз у вигляді:
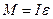 , (2.10)
, (2.10)
де 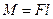 – момент сили
– момент сили 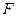 відносно точки О, l – плече сили,
відносно точки О, l – плече сили, 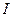 - момент інерції матеріальної точки
- момент інерції матеріальної точки 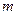 відносно точки О.
відносно точки О.
Вираз (2.10 ) за своїм виглядом є аналогом другого закону Ньютона для криволінійного руху з тією різницею, що аналогом сили 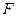 є момент сили
є момент сили 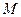 , маси
, маси 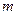 – момент інерції
– момент інерції 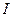 , прискорення
, прискорення 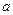 – кутове прискорення
– кутове прискорення 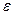 .
.
Оскільки точка рухається по колу сталого радіуса (r=const), то її момент інерції 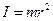 також сталий (I=const). Тоді вираз (2.10) можна звести до вигляду:
також сталий (I=const). Тоді вираз (2.10) можна звести до вигляду:
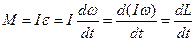 .
.
У векторному записі (рис.3)
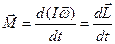 . (2.11)
. (2.11)
 Вектор
Вектор 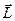 називають моментом імпульсу мате-ріальної точки відносно точки О. Даний вектор, який в умовах цієї задачі чисельно дорівнює
називають моментом імпульсу мате-ріальної точки відносно точки О. Даний вектор, який в умовах цієї задачі чисельно дорівнює 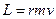 , є аналогом вектора імпульсу
, є аналогом вектора імпульсу 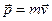 для прямолінійного руху.
для прямолінійного руху.
Розглянемо загаль-ний випадок, коли сила 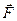 не лежить в одній площині з існуючою коловою траєкторією. За другим законом Ньютона рівняння руху матеріальної точки маси
не лежить в одній площині з існуючою коловою траєкторією. За другим законом Ньютона рівняння руху матеріальної точки маси 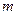 має вигляд:
має вигляд:
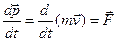
Домножимо даний вираз векторно на 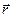 . Тут
. Тут 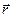 – радіус-вектор матеріальної точки масою m, проведений з деякої нерухомої точки О (центра обертання) до точки
– радіус-вектор матеріальної точки масою m, проведений з деякої нерухомої точки О (центра обертання) до точки 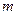 . Зауважимо, що
. Зауважимо, що 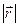 =const, оскільки розглядаємо лише обертовий рух. Тоді
=const, оскільки розглядаємо лише обертовий рух. Тоді
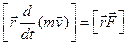
Ліву частину останнього виразу запишемо у вигляді:
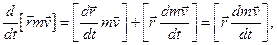 (2.12)
(2.12)
оскільки 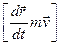 =
= 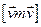 =0.
=0.
Вектор 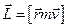 назвемо моментом імпульсу матеріальної точки відносно точки О, а вектор
назвемо моментом імпульсу матеріальної точки відносно точки О, а вектор 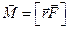 – моментом сили
– моментом сили 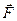 відносно точки О. Ввівши згадані позначення у вираз (2.12), отримаємо
відносно точки О. Ввівши згадані позначення у вираз (2.12), отримаємо
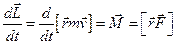 (2.13)
(2.13)
Вираз 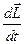 =
= 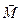 називають рівнянням моментів.
називають рівнянням моментів.
Після перетворення вираз (2.13) кінцево можна записати у вигляді, подібному до (2.10):
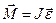 , (2.14)
, (2.14)
оскільки 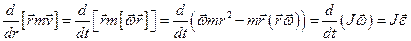 , а
, а 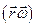 =0, бо
=0, бо 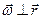 .
.
У останньому перетворенні використана відома формула для подвійного векторного добутку.
 |
Якщо через точку О провести довільну вісь z , то проекції векторів
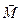 і
і 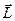 на цю вісь
на цю вісь 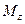 і
і 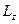 називають відповідно моментом сили
називають відповідно моментом сили 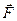 відносно осі z та моментом імпульсу матеріальної точки відносно осі
відносно осі z та моментом імпульсу матеріальної точки відносно осі 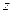 (рис.4 і рис.5).
(рис.4 і рис.5).
| <== попередня сторінка | | | наступна сторінка ==> |
| Закони динаміки системи матеріальних точок. Теорема про рух центра мас | | | Закон динаміки обертального руху абсолютно твердого тіла |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |