
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Рух в’язкої рідини. Ламінарна і турбулентна течія. Формула Пуазейля.
У реальній рідині під час руху одних шарів відносно інших виникають сили в’язкого тертя. Експериментально встановлено, що сили внутрішнього тертя між двома шарами рідини, що рухаються з різними швидкостями 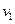 і
і 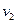 , можна описати за допомогою формули:
, можна описати за допомогою формули:
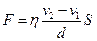 , (6.9)
, (6.9)
У виразі (6.9) 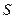 – площа шарів, що взаємодіють,
– площа шарів, що взаємодіють, 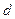 – відстань між шарами,
– відстань між шарами,
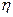 – динамічна в’язкість рідини (коефіцієнт пропорційності, залежний від сорту рідини, її стану, зокрема температури). Більш точніше дана залежність описується формулою Ньютона (див. вираз (3.7)):
– динамічна в’язкість рідини (коефіцієнт пропорційності, залежний від сорту рідини, її стану, зокрема температури). Більш точніше дана залежність описується формулою Ньютона (див. вираз (3.7)):
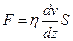 .
.
В’язкість рідини чисельно дорівнює силі тертя між двома шарами площею 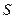 =1 при одиничному градієнті швидкості
=1 при одиничному градієнті швидкості 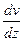 =1. Розмірність в’язкості
=1. Розмірність в’язкості 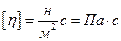 .
.
У багатьох задачах використовують величину 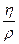 – коефіцієнт кінематичної в’язкості (
– коефіцієнт кінематичної в’язкості ( 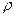 – густина рідини).
– густина рідини).
Розглядаючи рух рідини розрізняють два крайні типи течії рідини – ламінарну та турбулентну.
У ламінарній течії окремі шари рідини не змішуються між собою, ковзаючи один відносно одного. Ламінарна течія є стаціонарною.
Із збільшенням швидкості течії рідини ламінарна течія стає нестійкою і переходить у турбулентну. Під час турбулентного потоку частинки рідини рухаються складними траєкторіями, утворюючи вихори із замкненими траєкторіями, рідина інтенсивно перемішується.
Умови переходу від ламінарної до турбулентної течії характеризують числом Рейнольдса:
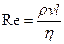 , (6.10)
, (6.10)
у якому 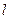 – характерний поперечний розмір тіла, що взаємодіє з рідиною. Для передбачення характеру руху рідини в конкретних задачах використовують розрахунок числа Рейнольдса. За малих величин
– характерний поперечний розмір тіла, що взаємодіє з рідиною. Для передбачення характеру руху рідини в конкретних задачах використовують розрахунок числа Рейнольдса. За малих величин 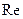 простежується ламінарна течія рідини. Починаючи з якогось критичного значення числа Рейнольдса течія рідини набуває турбулентного характеру.
простежується ламінарна течія рідини. Починаючи з якогось критичного значення числа Рейнольдса течія рідини набуває турбулентного характеру.
Зокрема, для води, що тече гладкою циліндричною трубою круглого перерізу діаметром 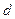 . критичне число Рейнольдса дорівнює :
. критичне число Рейнольдса дорівнює :
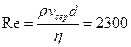 , (6.11)
, (6.11)
де 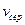 – середня швидкість течії рідини. Для води в трубі діаметром 0,02 м при
– середня швидкість течії рідини. Для води в трубі діаметром 0,02 м при 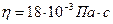 середня швидкість, при якій число Рейнольдса досягає критичного значення, дорівнює 0,2 м/с.
середня швидкість, при якій число Рейнольдса досягає критичного значення, дорівнює 0,2 м/с.
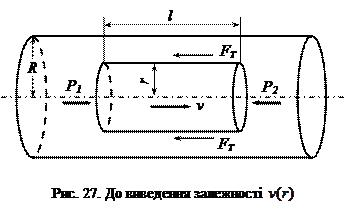 |
Проаналізуємо детальніше стаціонарну течію рідини в розміщеній горизонтально однорідній циліндричній трубі радіуса
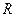 . Знайдемо закон зміни швидкості рідини
. Знайдемо закон зміни швидкості рідини 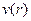 з відстанню від осі труби (
з відстанню від осі труби ( 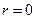 ) до її стінок (
) до її стінок ( 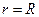 ). Уявно виділимо у рідині циліндричний об’єм радіуса
). Уявно виділимо у рідині циліндричний об’єм радіуса 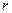 і довжиною
і довжиною 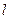 , вісь якого співпадає з віссю труби (рис. 27).
, вісь якого співпадає з віссю труби (рис. 27).
За умови стаціонарної течії рідини сумарна сила тиску 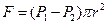 зрівноважується силою тертя
зрівноважується силою тертя 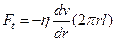 , де
, де 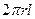 – площа бічної поверхні вибраного циліндра,
– площа бічної поверхні вибраного циліндра, 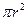 – площа основи циліндра,
– площа основи циліндра, 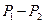 – перепад тиску між основами циліндра,
– перепад тиску між основами циліндра, 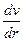 – градієнт швидкості. Запишемо цю умову у вигляді рівняння і знайдемо з нього
– градієнт швидкості. Запишемо цю умову у вигляді рівняння і знайдемо з нього 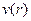 :
:
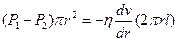 (6.12)
(6.12)
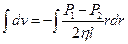
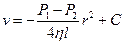 .
.
Оскільки швидкість рідини біля стінок дорівнює нулю ( 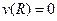 при
при 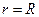 ), то
), то
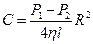 .
.
Отже:
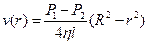 . (6.13)
. (6.13)
Якщо вважати, що швидкість рідини на осі труби 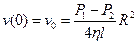 , то вираз (6.13) можна записати у вигляді:
, то вираз (6.13) можна записати у вигляді:

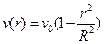 (6.14)
(6.14)
З виразу (6.14) видно, що залежність 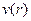 параболічна (рис. 28).
параболічна (рис. 28).
Вираз (6.13) можна використати для розрахунку об’єму рідини, що протікає через поперечний переріз труби за одиницю часу. Для цього поперечний переріз труби розіб’ємо на концентричні кільця радіуса 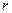
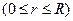 товщини
товщини 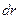 (рис. 29). Площа кільця дорівнює
(рис. 29). Площа кільця дорівнює 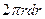 . За одиницю часу через поперечний переріз кільця протікає об’єм рідини
. За одиницю часу через поперечний переріз кільця протікає об’єм рідини 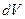 , який дорівнює:
, який дорівнює:
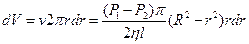 (6.15)
(6.15)
Знайдемо суму об’ємів рідини, яка пройшла за одиницю часу через повний поперечний переріз труби:
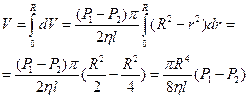 (6.16)
(6.16)
 Вираз (6.16) називають формулою Пуазейля. За допомогою цього виразу знаходять кількість (об’єм) рідини, що протікає через поперечний переріз круглої труби радіуса
Вираз (6.16) називають формулою Пуазейля. За допомогою цього виразу знаходять кількість (об’єм) рідини, що протікає через поперечний переріз круглої труби радіуса 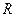 за одиницю часу. З виразу видно, що
за одиницю часу. З виразу видно, що 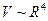 , а тому збільшення радіуса труби у два рази дозволяє збільшити пропускну здатність труби у 16 разів. Вираз (6.16) справедливий лише для ламінарної течії рідини.
, а тому збільшення радіуса труби у два рази дозволяє збільшити пропускну здатність труби у 16 разів. Вираз (6.16) справедливий лише для ламінарної течії рідини.
| <== попередня сторінка | | | наступна сторінка ==> |
| Основні поняття гідродинаміки. Стаціонарний рух рідини. Рівняння Бернуллі | | | Рух твердих тіл у рідинах |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |