
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Методичні вказівки для виконання роботи
1. Нехай нам дані емпіричні дані по 12 підприємствам деякої галузі у вигляді таблиці:
| V | K | L |
В якості одиниці виміру К обрана кількість одиниць устаткування, L – кількість людино-годин, V вимірюють у грошових одиницях.
Будемо шукати виробничу функцію Кобба-Дугласа
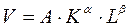 .
.
Щоб звести нашу задачу до побудови лінійної моделі, логарифмуємо:
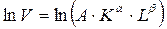 .
.
За властивостями логарифмів, отримуємо:
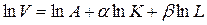 .
.
Виконуємо заміну:
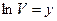 ,
, 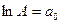 ,
, 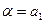 ,
, 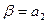 ,
,
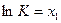 ,
, 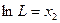 .
.
Переходимо до лінійної моделі:
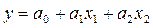 .
.
Таким чином, отримаємо наступну таблицю:
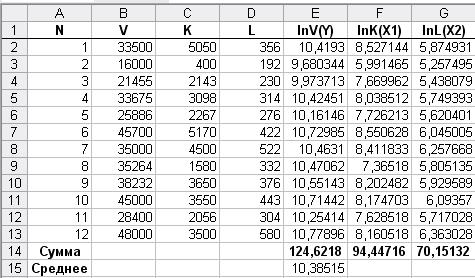
Тепер нам потрібно скласти систему нормальних рівнянь:
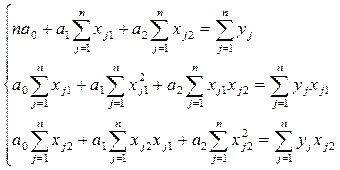
Запишемо нормальну систему традиційним способом, заповнивши таблицю:
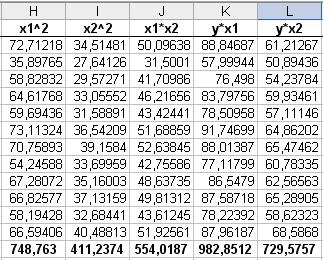
Після проведення потрібних обчислень система нормальних рівнянь буде мати вигляд:
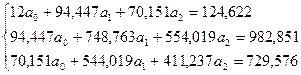
Для матриці коефіцієнтів знаходимо обернену матрицю, яка має назву кореляційної:
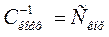
| 94,44716 | 70,15132 | ||
| Cкоеф | 94,44716 | 748,763 | 554,0187 |
| 70,15132 | 554,0187 | 411,2374 | |
Для того, щоб знайти кореляційну матрицю скористуємося функцією МОБР.
| 31,61357 | 0,802411 | -6,47384 | |
| Скор | 0,802411 | 0,438876 | -0,72813 |
| -6,47384 | -0,72813 | 2,087718 |
Далі знаходимо параметри 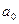 ,
, 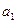 ,
, 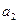 , перемноживши кореляційну матрицю
, перемноживши кореляційну матрицю 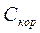 і стовпець вільних членів, скористуємося функцією МУМНОЖ.
і стовпець вільних членів, скористуємося функцією МУМНОЖ.
В нашому випадку стовпець вільних членів має вид:
| 124,6218 | |
| Свільн | 982,8512 |
| 729,5757 |
Тоді отримаємо наступні параметри 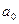 ,
, 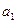 ,
, 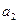 :
:
| а0 | 5,237621 |
| а1 | 0,119307 |
| а2 | 0,719904 |
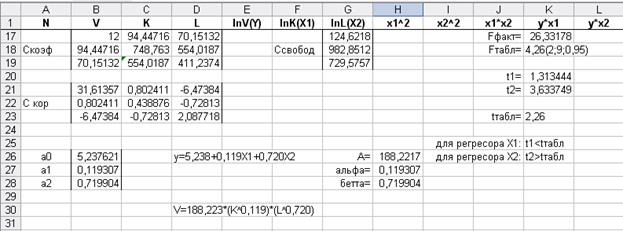
Отримаємо рівняння тренда лінеарізованої моделі:
y=5,238+0,119X1+0,720X2.
Робимо обернену заміну:
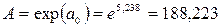 ;
;
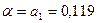 ;
;
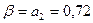 .
.
Тому виробнича функція Кобба-Дугласа має вигляд:
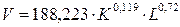 .
.
2. За допомогою критерію Фішера для рівня значущості 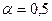 визначити адекватність знайденої моделі.
визначити адекватність знайденої моделі.
Для перевірки адекватності, дослідження значимості регресорів та знаходження довірчого проміжку використовують винятково лінеарізовану модель, а саме 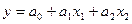 .
.
Справа в тому, що застосований математичний апарат розроблений для моделей, у яких параметри кореляційного рівняння входять лінійно.
Отже перевіримо адекватність. Для цього спочатку складемо наступну таблицю:
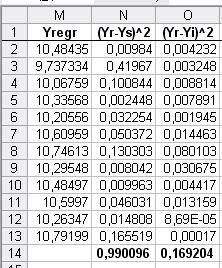
Для оцінки адекватності прийнятої економетричної моделі статистичним даним з надійністю Р=0,95 використовуємо критерій Фішера. Висуваємо гіпотезу Н0 про статистичну не значимість рівняння регресії, і нам треба її спростувати.
Знаходимо розрахункове значення величини  за формулою:
за формулою:
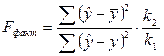 ,
,
де 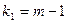 , а
, а 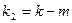 - кількість ступенів вільності, причому
- кількість ступенів вільності, причому 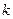 - число експериментів, а
- число експериментів, а 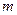 - число параметрів у кореляційному рівнянні. У нашому випадку
- число параметрів у кореляційному рівнянні. У нашому випадку
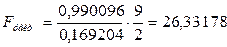
По таблицях розподілу Фішера знаходимо 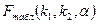 :
:
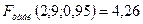 .
.
Оскільки Fфакт > Fтабл, 26,33 >4,26, робимо висновок про те, що математична модель з надійністю 0,95 адекватна емпіричним даним.
3. За допомогою критерію Стьюдента визначити значущість регресорів.
Тепер перевіримо значущість регресорів. З цією метою для кожного регресора знаходимо величину:
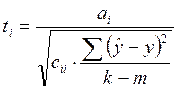
Тут: 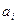 - коефіцієнт регресору
- коефіцієнт регресору  ;
;
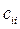 - відповідний діагональний елемент матриці
- відповідний діагональний елемент матриці 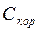 (верхній лівий елемент розуміють як
(верхній лівий елемент розуміють як 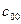 ).
).
Отримаємо:
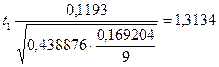 ;
;
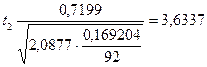 .
.
З таблиць розподілу Стьюдента для кількості ступенів вільності 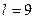 й імовірності 0,95 маємо:
й імовірності 0,95 маємо: 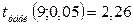 .
.
Якщо 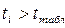 , то регресор вважають значимим, у протилежному випадку роблять висновок про те, що регресор не впливає істотно на регресант.
, то регресор вважають значимим, у протилежному випадку роблять висновок про те, що регресор не впливає істотно на регресант.
В нашому випадку  та
та 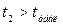 . Це означає, що в досліджуваній галузі вирішальну роль у збільшенні прибутку грає додаткове залучення живої праці L, а не витрати на виробничі фонди K.
. Це означає, що в досліджуваній галузі вирішальну роль у збільшенні прибутку грає додаткове залучення живої праці L, а не витрати на виробничі фонди K.
4. Зробити точковий та інтервальний прогнози для наведених у кінці кожного варіанта значень регресорів з надійністю 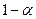 (
( 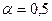 ).
).
Знайдемо прогнозне значення виробничої функції, якщо основні виробничі фонди складають 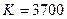 одиниць устаткування, а витрати праці
одиниць устаткування, а витрати праці 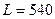 людино-годин. Оскільки для цього необхідно скористатися лінійною моделлю, знаходимо:
людино-годин. Оскільки для цього необхідно скористатися лінійною моделлю, знаходимо:
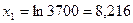 ;
;
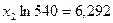 .
.
Підставляючи ці значення в лінійне рівняння регресії, отримаємо точкову оцінку:
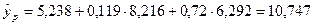 .
.
Точкова оцінка для обсягу продукції складе:
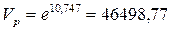 грошових одиниць.
грошових одиниць.
Інтервал довіри з надійністю 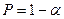 знаходять таким чином:
знаходять таким чином:
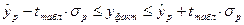 .
.
де 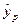 - точкова оцінка регресанту, що отримана з рівняння регресії, яке відповідає обраним значенням регресорів
- точкова оцінка регресанту, що отримана з рівняння регресії, яке відповідає обраним значенням регресорів 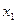 ,
, 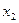 ;
;
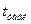 - критичне значення при заданому
- критичне значення при заданому  для величини, що має розподіл Стьюдента.
для величини, що має розподіл Стьюдента.
Розрахункова дисперсія 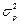 обчислюється за формулою:
обчислюється за формулою:
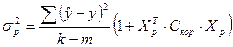 ,
,
де 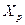 - 3-вимірний вектор (стовпець), перша координата якого дорівнює 1, інші координати – обраним значенням регресорів
- 3-вимірний вектор (стовпець), перша координата якого дорівнює 1, інші координати – обраним значенням регресорів 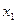 ,
, 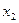 , тобто він має вигляд:
, тобто він має вигляд:
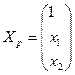 .
.
У нашому випадку отримаємо:
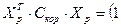
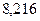
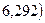
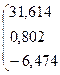
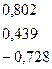
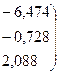
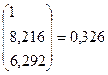 ;
;
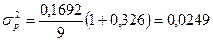 .
.
Звідси
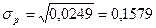 .
.
(середня стандартна помилка)
Знайдемо граничну помилку:
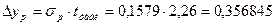 ;
;
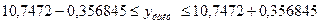 ;
;
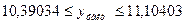 .
.
Тепер знаходимо інтервал довіри для регресанту V:
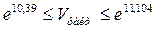 ;
;
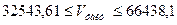 .
.
Таким чином, з надійністю 0,95 можна стверджувати, що фактичне значення регресанту V для 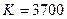 і
і 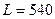 буде знаходитися в проміжку
буде знаходитися в проміжку 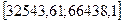 .
.

| <== попередня сторінка | | | наступна сторінка ==> |
| Лабораторна робота № 5 | | | Варіанти для самостійного виконання |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |