• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Приклад 1. Виробнича функція Кобба — Дугласа

Виробнича функція — це економетрична модель, яка кількісно описує зв’язок основних результативних показників виробничо-господарської діяльності з факторами, що визначають ці показники. До основних показників можна віднести дохід, прибуток, рентабельність, продуктивність праці, собівартість і т.ін.

Перше поняття виробничої функції пов’язане з математичним моделюванням технологічної залежності між обсягом продукції, що випускається, і кількісними характеристиками витрат ресурсів. Звідси і назва функції «виробнича». Уперше така функція була побудована американськими дослідниками Коббом і Дугласом ще в 30-ті роки ХХ ст. за даними про функціонування обробної промисловості США протягом двадцяти років і є класичним прикладом економетричного моделювання.

Функція Кобба — Дугласа (CDPF) належить до найвідоміших виробничих функцій, що набули широкого застосування в економічних дослідженнях, особливо на макрорівні. Класична виробнича функція Кобба — Дугласа має вигляд

Y =aF^aL^1–a,(4)

де Y — обсяг продукції; F — основний капітал; L — робоча сила.

У цій функції параметри a, a і 1—a є невід’ємними. Таке твердження можна довести, якщо з виробничої функції виключити один з факторів. Для цього, поділивши ліву і праву частини залежності Y= f(F,L) на L, дістанемо функцію двох змінних

W=f(V),

де 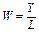— продуктивність праці; 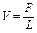— фондоозброєність праці.

Нехай залежність між W і V має вигляд степеневої функції, тобто

W = aV^a.

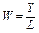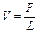Підставивши в цю функцію і , дістанемо:

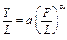, або Y = aF^aL^{1 – a}.

Сума параметрів або степінь однорідності, класичної функції Кобба — Дугласа дорівнює одиниці. А це означає, що при збільшенні обох виробничих ресурсів на одиницю обсяг продукції також збільшиться на одиницю. Отже, ефективність ресурсів у такому разі стала.

Практичні дослідження функції Кобба — Дугласа показали, що припущення про лінійну однорідність на практиці виконується рідко. Тому була запропонована виробнича функція загальнішого вигляду

Y =aF^aL^b. (5)

Сума параметрів (a+b) на відміну від попереднього випадку може бути як меншою, так і більшою від одиниці. Якщо (a + b) > 1, то темпи росту обсягу продукції вищі за темпи росту виробничих ресурсів, а якщо (a + b) < 1, то, навпаки, темпи росту продукції нижчі за темпи росту ресурсів.

Припустимо,що рівень кожного виробничого ресурсу збільшився на r %, тоді величини їх дорівнюватимуть 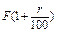і .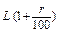

Обсяг продукції на основі виробничої функції запишеться так:

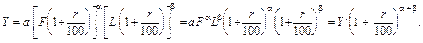
Звідси при a + b > 1 обсяг продукції зростає більш ніж на r %; при a + b < 1 — менш ніж на r %; при a + b = 1 продукція збільшиться на r %. Визначивши окремі коефіцієнти еластичності для виробничої функції Кобба — Дугласа, дістанемо:

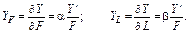
Це означає, що граничний приріст продукції за рахунок приросту кожного ресурсу визначається як добуток коефіцієнта еластичності на середню ефективність ресурсу. Параметр a у функції Кобба — Дугласа залежить од вибраних одиниць вимірювання Y, F, L; водночас числове значення цього параметра визначається також ефективністю виробничого процесу. У цьому можна переконатись, порівнявши дві виробничі функції, які відрізняються одна від одної лише значенням параметра a.

Для фіксованих значень F і L тій функції, в якої більше числове значення параметра a, відповідає більше значення Y. Отже, і виробничий процес, який описується цією функцією, буде ефективнішим. Другі похідні функції Кобба — Дугласа мають такий вигляд:

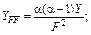
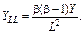
Узявши до уваги, що 0 < a < 1 і 0<b<1, Y_FF < 0 і Y_LL < 0, дійдемо висновку: при збільшенні ресурсів граничний приріст обсягу продукції зменшуватиметься. Якщо обсяг продукції у функції Кобба — Дугласа вважати сталим (таким, що дорівнює const), то можна обчислити граничні норми заміщення ресурсів:

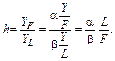
Звідси бачимо, що гранична норма заміщення ресурсів у функції
Кобба — Дугласа визначається як добуток співвідношень величин ресурсів та їх коефіцієнтів еластичності.

Швидкість зміни норми заміщення ресурсів у зв’язку зі зміною величини ресурсів обчислюється так:

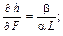
Мірою швидкості зміни h є еластичність заміщення ресурсів F і L, що визначається як відношення зміни величини ресурсів до зміни величини h:

.

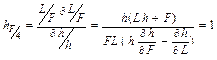Отже, еластичність заміщення в кожній точці кривої, що характеризує виробничу функцію Кобба — Дугласа, дорівнює одиниці.

Розглянемо тепер поводження функції при зміні масштабу виробництва. Для цього припустимо, що витрати кожного ресурсу виробництва збільшилися в l раз, тоді нове значення Y визначатиметься так:

Y=a(lF)^a(lL)^b=l^a+bY.

Степінь однорідності цієї функції дорівнює a+b. Якщо a+b=1, то рівень ефективності ресурсів не залежить від масштабів виробництва. Якщо a+b<1, то з розширенням масштабів виробництва середні витрати в розрахунку на одиницю продукції зменшуються, а при a+b>1 — збільшуються. Причому ці властивості не залежать від числових значень F і L і зберігають силу в кожній точці виробничої функції.

За припущення, що мета господарської діяльності — максимізація прибутку, можна проілюструвати інші властивості виробничої функції. Запишемо функцію прибутку:

П=bY ^r+1–wL – rF+l[ f(F,L) – Y ].

Підприємець вибирає такі значення Y, L, F, які максимізують прибуток при обмеженнях, що накладаються виробничою функцією. Величини b, w, r— параметри функції прибутку, l — множник Лагранжа. Якщо виробничий процес у даному співвідношенні описується функцією Кобба — Дугласа, то можна записати умови максимізації прибутку:

,

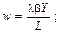
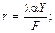
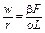l = (r + 1)P при r ¹ – 1, де P = bY ^r.

Звідси обсяги ресурсів такі:

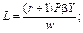
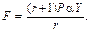
У такому випадку максимальне значення випуску продукції, якщо a + b ¹ 1, можна записати так:

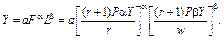
При r=1згідно із записаними щойно умовами максимізації дістанемо:

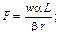
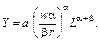
Отже, необхідні умови для забезпечення максимізації прибутку дають змогу визначити відповідні витрати робочої сили і основного капіталу. З розширенням масштабів виробництва ефективність витрат ресурсів падає, що відповідає максимізації прибутку в умовах досконалої конкуренції. Наведений приклад виробничої функції показує, що ця економетрична модель дає змогу досить широко проаналізувати виробничу діяльність, визначити шляхи її вдосконалення з метою підвищення ефективності. Обгрунтованість такого аналізу повністю залежить од вірогідності економетричної моделі, від того, наскільки вона адекватна реальному процесу.

Проблема побудови виробничої функції або інших технологічних взаємозалежностей у виробництві — класична проблема економетрії, висвітлюється далі.

Приклад 2. Моделі пропозиції і попиту
на конкурентному ринку

На конкурентному ринку рівновага обміну встановлюється через рівновагу між пропозицією і попитом. Нехай g₁ і g₂ — кількість попиту і пропозиції деякого продукту в певний день на деякому ринку; p — ціна, за якою реалізується продукція. Величини g₁ і g₂ залежать від p, оскільки ціна не влаштовує покупців і продавців, то кількість проданого товару зменшується. У результаті можна записати дві функції:

g₁=f(p, u) — функцію попиту;

g₂=Y(p, e) — функцію пропозиції.

Знаючи ціну p, можна визначити величини попиту і пропозиції. Для існування рівноваги на ринку необхідно, щоб виконувалась рівність. Отже, модель має такий вигляд:

g₁=g₂ ;

g₁=f(p, u); (6)

g₂=Y(p, e).

До неї входять дві функції, що характеризують залежність попиту і пропозиції від ціни, а також тотожність.

В реальних умовах попит і пропозиція певного товару залежать не лише від його ціни, а й від цін товарів, які можуть заміняти або доповнювати розглядуваний товар. Попит і пропозиція залежать також від інших чинників, наприклад, попит залежить від доходу покупців, а пропозиція від виробничих умов і т.ін. Тоді модель (2.6) можна записати так:

g_1t = f(p_t , X_1t , X_2t , ... X_mt , u_t);

g_2t = Y(p_{t – 1}, X_1t , X_2t , ... X_mt , e_t ); (7)

g_1t = g_2t .

В цій моделі на відміну від попередньої попит у періоді t залежить від ціни в цьому самому періоді, а пропозиція в періоді t залежить від ціни попереднього періоду (t – 1).

Нехай залежність попиту і пропозиції від факторів, що впливають на них, лінійна. Тоді економетрична модель запишеться так:

g_1t=a₀+a₁p_t+a₂X_1t+a₃X_2t+ ... + a_m X_mt+u_t ;

g_2t = b₀ + b₁p_{t – 1} + b₂X_1t + b₃X_2t + ... + b_m X_mt + e_t ; (8)

g_1t=g_2t .

Щоб оцінити параметри цієї моделі, необхідно застосувати один з численних економетричних методів, які розглядаються далі.

Переглядів: 6330