• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Випадкова складова економетричної моделі

Розглянемо економетричну модель з двома змінними у загальному вигляді:

Y =f(X)+u, (15)

де Y — залежна змінна; X — незалежна змінна; u — випадкова складова.

Це означає, що ми ідентифікували змінну X, яка впливає на змінну Y. Назвемо таку економетричну модель простою моделлю.

Як відомо, численні взаємозв’язки між економічними показниками не можна формалізувати лише на базі простої економетричної моделі. Наведені раніше приклади економетричних моделей показують, що вони описують вплив багатьох чинників на економічні процеси та явища. Причому для формалізації цих зв’язків може використовуватись не одне рівняння, а їх система.

На базі простої економетричної моделі розглянемо принципову структуру економетричної моделі та основні методи оцінювання її параметрів. Змістовне тлумачення взаємозв’язку між економічними показниками [модель (15)] має підказати його конкретну аналітичну форму. Але оскільки одні й ті самі економічні умови можуть задовольняти різні функції, то краще звернутися до статистичного аналізу і з його допомогою зробити вибір серед можливих альтернативних варіантів.

Найпростішою є лінійна форма зв’язку між двома змінними:

Y =a₀+bX ,

де a₀ і a₁ — невідомі параметри, перший з яких визначає довжину відрізка, утворюваного перетином прямої з віссю ординат, а другий — тангенс кута нахилу цієї прямої до осі абсцис.

Можливі й інші форми залежностей між двома змінними, наприклад:

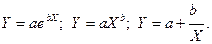
Останнє з цих співвідношень є лінійним відносно 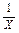, а перші два можна звести до лінійної форми для перетворених змінних, якщо взяти логарифми від виразів в обох частинах кожного з рівнянь:

lnY =lna+bX;

lnY =lna+bnX.

Навіть побіжне знайомство з економічними показниками, взаємозв’язок між якими вимірюється, показує, що окремі експериментальні значення залежної змінної не можуть міститися строго на прямій лінії чи на графіку функції іншої форми. Певна частина фактичних спостережень над змінною лежатиме вище або нижче від значень, обчислених згідно з вибраною функцією. Якщо фактичні значення залежної змінної містяться на значній відстані від обчислених з допомогою функції, то можна припустити, що формалізація залежності між економічними показниками на основі функції типу (15) чи якоїсь іншої функції не адекватна реальному процесу взаємозв’язків в економіці. Проте поняття «значна відстань» не є конкретним, а тому не може бути критерієм для оцінювання адекватності моделі.

Щоб розв’язати цю задачу, до економетричної моделі вводять стохастичну складову, яка акумулює в собі всі відхилення фактичних спостережень змінної Y від обчислених згідно з моделлю.

Математичний аналіз цієї складової дасть змогу зробити висновок щодо того, чи можна вважати її стохастичною і чи містить вона систематичну частину відхилень, яка може бути зумовлена наявністю тих чи інших помилок у моделюванні.

Нехай вектор змінної Y описує витрати на споживання, а вектор X — величину доходу сім’ї. Очевидно, що для окремих груп сімей існує певна залежність між споживчими витратами і доходом сім’ї. Проте, як уже зазначалося, на розмір споживчих витрат крім доходу можуть впливати інші фактори, частина яких є випадковими. Ці фактори й зумовлюють відхилення фактичних витрат на споживання від обчислених, наприклад, на основі регресійної функції:

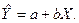(16)

Наблизити обчислені значення до фактичних формально можна введенням до моделі стохастичної складової:

Y =a+bX+u. (17)

У моделі (17) символом u позначено змінну, яка може набувати додатних та від’ємних значень, оскільки вона вимірює відхилення витрат на споживання кожної окремої сім’ї від обчисленого значення згідно з (16).

зауважимо, що в моделі (17) a і b— оцінювані параметри, а в моделі (16) 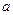і 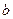— їх оцінки.

Означення 1. Стохастичну складову u економетричної моделі називають помилкою (залишком, збуренням, відхиленням).

Введення до моделі (17) стохастичної складової має три підстави, кожна з яких не виключає решти двох.

1. Величину витрат на споживання визначає не лише рівень доходів, а й інші об’єктивні чинники, наприклад розмір сім’ї, середній вік і т.ін.;

2. На величину споживання впливають випадкові фактори, наприклад схильність до ощадливості, стриманість чи навпаки — надмірність у витратах і т.ін.;

3. Частина факторів, які впливають на величину споживчих витрат, не оцінюються кількісно, вони не квантифікуються. Крім того, можлива помилка вимірювання змінних.

Отже, замість залежності

Y =f(x₁, x₂, x₃ ... x_m),

де m — досить велике, розглядається модель з невеликим числом незалежних змінних, причому Y відіграє роль функції від найважливіших 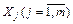, тоді як чистий сумарний ефект від впливу всіх інших чинників відбиває змінна u. У крайньому разі, якщо лишається одна незалежна змінна, маємо:

Y =f(X, u). (18)

У класичній лінійній економетричній моделі змінна u інтерпретується як випадкова змінна, яка має розподіл з математичним сподіванням, що дорівнює нулю, і сталою дисперсією 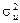. Це дає змогу розглядати змінну u як стохастичне збурення (помилку, відхилення). З огляду на те, що u охоплює вплив багатьох чинників, які можна вважати незалежними, на підставі центральної граничної теореми теорії ймовірностей, доходимо висновку: стохастична складова економетричної моделі розподілена за нормальним законом.

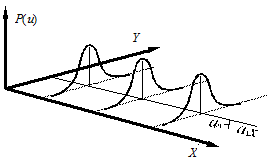Рис. 2.1.Розділ залишків

Щодо нашого прикладу, коли витрати на споживання перебувають у лінійній залежності від доходу сімей, а змінна u є випадковою складовою, можна графічно зобразити цю залежність за умови, що величина доходів упорядкована від меншого значення до більшого (рис. 2.1).

Розподіл імовірностей P(u) групуватиметься при цьому навколо лінії регресії 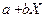. Можливо, у цьому прикладі доцільніше було б припускати, що дисперсія відхилення u зростає зі збільшенням доходу X. Цю особливість розглянемо пізніше, бо вона може бути притаманна й іншим економічним залежностям (наприклад, залежності заощаджень від доходу, дивідендів від прибутку і т.ін.).

В економетричній моделі (16) параметри 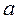, 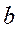невідомі. На підставі вибіркових спостережень X і Y потрібно не лише статистично оцінити ці параметри, а й перевірити виконання щодо них деяких гіпотез:

1) Чи можна вважати споживання пропорційними до доходу ( 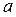= 0)?

2) Чи буде гранична схильність до споживання ( 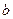) більша за половину?

3) Чи виправдана для цієї вибіркової сукупності гіпотеза про сталу дисперсію залишків для всіх значень X ?

Усі наведені щойно запитання є типовими задачами економетричних досліджень, і основна мета економетрії — вивчити класичні методи розв’язування поставлених задач, а також опанувати нові методи розв’язування складніших економічних задач, які максимально наближені до реальних умов.

Питання для самоконтролю.

1.З яких елементів складається математична модель?

2.Назвіть типи математичних моделей. Чим вони різняться між собою?

3.До якого типу математичних моделей належить економетрична модель?

4.Які особливості має економетрична модель?

5.Як треба розуміти сукупність спостережень та її однорідність?

6.Чим забезпечується порівнянність даних у просторі і часі?

7.Як визначається набір змінних для побудови економетричної моделі?

8.Наведіть декілька прикладів економетричних моделей.

9.Дайте тлумачення випадкової складової економетричної моделі.

10.Які методи застосовуються для оцінювання параметрів класичної регресійної моделі?

11.У чому сутність методу найменших квадратів (1МНК)?

12.Запишіть альтернативні варіанти оцінювання параметрів моделі методом 1МНК.

13.Як можна інтерпретувати параметри простої економетричної моделі?

Переглядів: 2307