• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Множинний коефіцієнт кореляції і детермінації

Тіснота зв’язку загального впливу всіх незалежних змінних на залежну визначається коефіцієнтами детермінації і множинної кореляції.

Щоб дати метод їх розрахунку необхідно показати, що варіація залежної змінної (Y) навколо свого вибіркового середнього значення ( 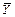)* може бути розкладена на дві складові:

1) варіацію розрахункових значень ( 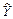) навколо середнього значення ;

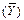2) варіацію розрахункових значень ( 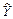) навколо фактичних (Y).

Необхідні при цьому обчислення зведемо в табл.2.

Таблиця 2

Джерело варіації	Сума квадратів відхилень	Ступені свободи	Середнє квадратів відхилень або дисперсія
Факторна ( )
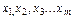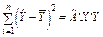
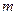
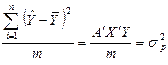
Залишок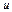
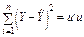
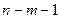
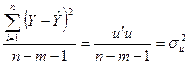
Загальна варіація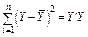

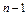
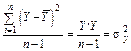
Зауважимо, що всі змінні Y i X взяті як відхилення від свого середнього значення.

Використаємо середні квадратів відхилень (дисперсії) (див. табл. 2) і запишемо формулу для обчислення коефіцієнта детермінації:

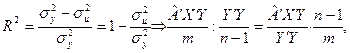(8)

або, не враховуючи ступенів свободи:

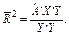(9)

Оскільки у (8) задані незміщені оцінки дисперсії з урахуванням числа ступенів свободи, то коефіцієнт детермінації може зменшуватись при введені в модель нових незалежних змінних. Тоді як для коефіцієнта детермінації, обчисленого без урахування поправки (n – 1/m – 1) на число ступенів свободи (9), коефіцієнт детермінації ніколи не зменшується. Залежність між цими двома коефіцієнтами можна подати так:

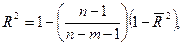(10)

де 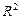— коефіцієнт детермінації з урахуванням числа ступенів свободи;

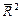— коефіцієнт детермінації без урахування числа ступенів свободи.

Для функції з двома і більше незалежними змінними коефіцієнт детермінації може набувати значень на множині 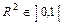. Числове значення коефіцієнта детермінації характеризує, якою мірою варіація залежної змінної ( 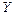) визначається варіацією незалежних змінних. Чим ближчий він до одиниці, тим більше варіація залежної змінної визначається варіацією незалежних змінних.

Множинний коефіцієнт кореляції:

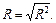
Він характеризує тісноту зв’язку усіх незалежних змінних із залежною.

Для множинного коефіцієнта кореляції з урахуваннням і без урахуванння числа ступенів свободи характерна така сама зміна числового значення, як і для коефіцієнта детермінації.

Розглянемо альтернативний спосіб обчислення коефіцієнтів детермінації і кореляції, коли система нормальних рівнянь будується на основі коефіцієнтів парної кореляції .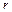

У такому разі оцінку параметрів моделі можна записати:

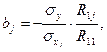(11)

де 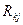— алгебраїчне доповнення матриці 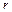до елемента .

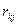Сума квадратів відхилень (залишків) також може бути виражена через алгебраїчне доповнення матриці :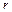

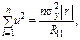
де 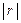— визначник кореляційної матриці. А це, у свою чергу, дає нам альтернативний вираз для коефіцієнта детермінації:

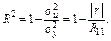(12)

Ще один альтернативний метод розрахунку коефіцієнтів детермінації на основі матриці 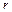можна подати у вигляді

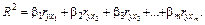(13)

Звідси коефіцієнт кореляції

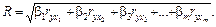(14)

4. Частинні коефіцієнти кореляції
і коефіцієнти регресії

Частинні коефіцієнти кореляції так само, як і парні, характеризують тісноту зв’язку між двома змінними. Але на відміну від парних частинні коефіцієнти характеризують тісноту зв’язку за умови, що інші незалежні змінні сталі.

Можна дістати спрощений вираз для розрахунку коефіцієнта частинної кореляції, обравши інший спосіб інтерпретації цього коефіцієнта. Для випадку простої регресії двох змінних маємо

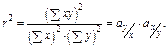
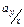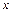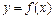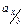де характеризує коефіцієнт при у рівнянні , а — коефіцієнт при 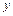в рівнянні 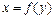. Отже, квадрат коефіцієнта парної кореляції дорівнює добутку двох наведених коефіцієнтів. Коефіцієнт частинної кореляції можна визначити аналогічно. Наприклад, розглянемо два регресійні рівняння:

;

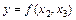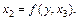
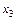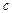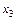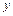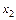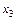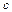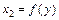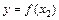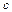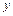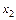Нехай в цих рівняннях дорівнює деякій довільній величині , тоді член, який відповідає змінній збігатиметься з вільним членом, а отже, дістанемо дві прості регресії, які відбивають загальну зміну і на площині = . Оскільки модель є лінійною, то коефіцієнти регресії і лишаються незмінними при різних значеннях , тобто можна стверджувати: квадрат коефіцієнта частинної кореляції між і дорівнює добутку коефіцієнтів при 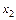і 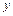у двох множинних регресіях.

Згідно з (8) запишемо ці рівняння у вигляді

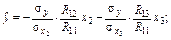
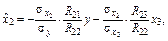
де 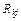— алгебраїчні доповнення до елемента 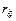матриці .

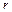Звідси

.

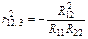Для знаходження частинного коефіцієнта кореляції змінної y з x₂ за умови, що змінна x₃ стала, достатньо взяти добуток параметрів при x₂ і y в наведених щойно рівняннях з протилежним знаком.

Аналогічно

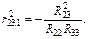
Тоді частинні коефіцієнти кореляції будуть такі:

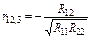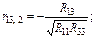
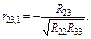; (15)

Ці висновки можна поширити на випадок, коли економетрична модель має 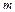незалежних змінних 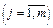, але при цьому решта незалежних змінних (крім двох) є константами.

Переглядів: 5814