• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Розкладення виразів.

Під розкладенням виразу розуміють математичне перетворення, яке переводить степені і добутки у більш прості для аналізу суми. У випадку розкладення тригонометричних виразів, функціі кратного аргументу перетворюються у відповідні їм функції від одинарного аргументу. Для розкладення логарифмічних функцій, використовуються відповідні формули логарифмічних спрощень.

Для проведення розкладу в MahCad існує спеціальний оператор Expand (Розкласти) панелі Symbolic (Символьні). В лівий маркер даного оператора заноситься вираз, який ми плануємо розкласти, а в правий – змінна або вираз, відносно якої відбувається розклад. Якщо вираз треба спростити максимально – правий маркер можна просто видалити, і система виконає розкладення по максимуму. Якщо спрощення потрібно провести лише до певного моменту, не до кінця, - потрібно в правому маркеру вказати ту частину виразу, яка повинна лишитися незмінною. Також можна спочатку ввести вираз, який потрібно розкласти, а потім ввести оператор Expand. Приклади розкладення різних типів виразів:

1. Розкладення алгебраїчного виразу.

Система перемножує вираз в чисельнику, зводить чисельник до спільного знаменника. Розкриває степінь в знаменнику, після чого чисельник ділиться на знаменник.

- Розглянемо різницю в результаті при заповненні правого маркера Expand, куди введемо (х):

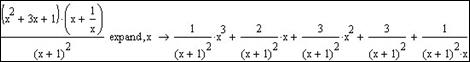у випадку розкладення дробів, заповнений правий маркер означає, що кожний елемент чисельника буде розділений на знаменник.

1. Розкладення тригонометричного виразу.

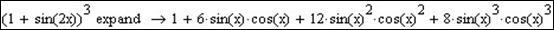
- Розглянемо різницю в результаті при заповненні правого маркера Expand, куди введемо (2х):

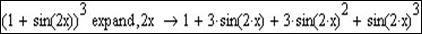
3. Розкладення тригонометричного виразу.

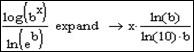Зверніть увагу на те, що десятковий логарифм представляється через відношення натуральних логарифмів.

У випадку роботи з логарифмами, використання оператора Expand є не завжди зручним, тому, що регенеруються лише натуральні логарифми за формулою 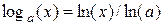. Обійти цей недолік системи – неможливо. Слід просто замінювати відношення натуральних логарифмів на логарифми з потрібною основою за даною формулою.

Крім свого прямого призначення, оператор Expand можна використовувати в якості довідника математичних формул по символьній алгебрі (особливо тригонометрії). Наприклад:

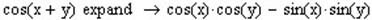
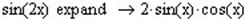
1. Розкладення на множники та зведення до спільного знаменника.

Для проведення розкладу на множники в MahCad існує спеціальний оператор Factor (від factoring – розкласти на множники)панелі Symbolic (Символьні). За допомогою оператора Factor не можна перетворити логарифмічний або тригонометричний вираз. Розкласти на множники можна тільки не дуже складний алгебраїчний вираз.

Оператор Factor має таке ж саме задання як і оператор Expand. Різниця в тому, що правий маркер потрібно обов’язково видалити, інакше результат не буде отримано.

Розкладення на множники не працює з комплексними числами. Можна розкласти лише на дійсні множники. Можливий розклад і в тому випадку, коли у вираз входять спеціальні функції, наприклад тригонометричні, коли система може використати до них звичайні алгебраїчні правила розкладу на множники.

1. Приклади розкладання на множники:

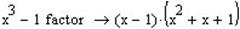
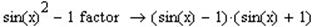
Другою важливою операцією яку виконує оператор Factor є розклад цілих чисел на прості множники.

2. Приклад розкладання чисел: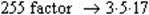

Ще однією важливою операцією, яку виконує Factor є перетворення десяткових дробів в прості дроби.

3. Приклад переведення дробів:

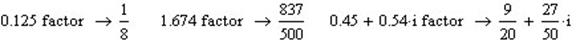
Оператор Factor використовується також для зведення до спільного знаменника. При чому в чисельник і знаменник дробів можуть входити будь-які функції та їх поєднання.

4. Приклад зведення дробів до спільного знаменника.

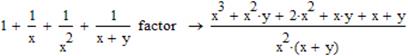
1. Винесення спільного множника за дужки.

Винесення спільного множника за дужки виконує оператор Collect (Збирати) панелі Symbolic (Символьні). Вводиться так само, як попередні оператори. В маркері зліва вказуємо вираз, з якого будемо виносити спільний множник, справа – ім’я змінної або функції, по якій проводимо дане перетворення. Винесення спільного множника може бути здійснене лише по одній змінній. Якщо доданки потрібно розподілити по декільком групам, то вираз потрібно буде ділити на частини і оперувати з кожною з них окремо.

Зазвичай, оператор Collect об’єднує в одну групу члени, в яких змінна, по якій здійснюється перетворення, входить в однаковому степені. В оператор Collect неможливо вказати вираз, який ви хочете винести за дужки. Тому він використовується лише для елементарних спрощень.

Приклад винесення спільного множника за дужки:

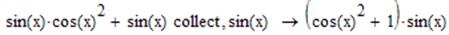
1. Розкладення на елементарні дроби.

Для розкладення виразу на елементарні дроби в MathCad використовують оператор Parfrac (елементарні дроби) панелі Symbolic. В лівому маркері оператора прописуємо вираз, який потребує спрощення, в правому – змінна, виходячи з якої повинно бути проведено спрощення. В якості змінних можуть бути використані функції.

Приклад розкладу на елементарні дроби:

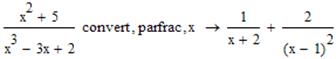
1. Виконання підстановки та заміни змінних.

Для виконання підстановки в MathCad використовують оператор Substitute (Замістити) панелі Symbolic (Символьні).

Вводиться оператор так само, як і попередні оператори. В правому маркері робимо запис: a=b, де b – вираз або значення, яке ми підставляємо на місце змінної a. Якщо потрібно замінити дві змінні, то через кому робимо ще одне аналогічне присвоєння. Але замість звичайного дорівнює ставимо дорівнює з панелі Boolean (Булеві). Оператор Substitute працює як із змінними, так і з функціями. ( ). Слід зауважити, що система погано працює з коренями.

Приклад підстановки:

1. Комплексне спрощення виразів.

Спрощення, для здійснення якого потрібно виконати декілька операцій різного роду, будемо називати комплексним спрощенням.

В простих випадках аналітичний процесор MathCad здатний проводити комплексне спрощення самостійно. Для цього служить спеціальний символьний оператор Simplify (Спростити),панелі Symbolic. Можливості оператора Simplify суміщають в собі можливості вивчених попередньо операторів. Крім того, оператор Simplify може зводити подібні доданки, та виконувати арифметичні обрахунки, суміщає всі виконані операції таким чином, щоб спрощення було максимальним.

Простий приклад:

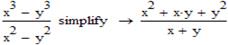
За умовчанням MathCad сприймає всі змінні як комплексні числа, тому у випадках, коли спрощення залежить від того, які значення може приймати змінна (вирази з коренем, логарифмічні вирази), потрібно наперед обумовити можливі значення або параметри змінної.

Для цього в MathCad є спеціальний оператор Modifier (Модифікація) панелі Symbolic. Він відкривається у вигляді окремої панелі, що складається з чотирьох операторів. ((Відкрили, подивилися)). Вводити їх можна як з панелі так і з клавіатури. Розглянемо кожен з них:

- Assume(Прийняти) слово – заготовка для створення оператора модифікації.

- Real(Дійсне) описує змінну як дійсне число.

- RealRange (a,b) (Дійсна область) дозволяє обмежити область визначення змінної або константи відрізком між дійсними числами a і b.

- Trig (Тригонометричні) розглядає змінну як тригонометричну величину. На практиці використовується рідко, так як реально практично ні на що не впливає.

НайкращеMathCad спрощує арифметичні та логарифмічні вирази. Погано працює з коренями та тригонометричними функціями. Якщо вам потрібно спростити складний вираз, потрібно скеровувати програму в потрібному напрямку. Розглянемо Приклад 1:

Спростити вираз:

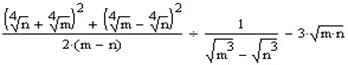
Оперувати таким великим виразом досить непросто. Тому розділимо його на три частини і будемо проводити спрощення поетапно. В першу чергу будемо розкривати квадрати в чисельнику першої частини виразу.

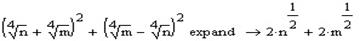
ОператорSimplify погано працює з коренями та дробовими степенями то ми надалі виконаємо заміну (m=x², n=y²), накладемо проміжок значень змінної (x≥0, y≥0), та спростимо (Simplify).

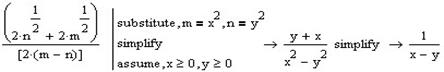
Виконаємо заміну в другій частині виразу:

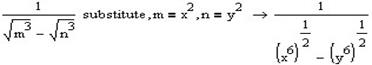
Спростимо її разом із першою частиною, яку ми спростили попередньо:

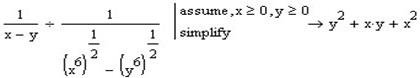
Виконаємо заміну в третій частині виразу :

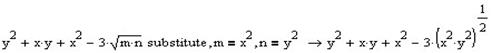
Та спростимо її разом з попередньою:

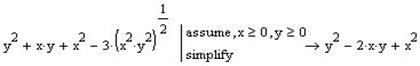
Розкладаємо отриманий вираз на множники та виконуємо зворотню заміну:

.

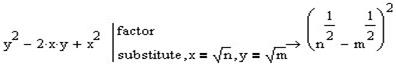Приклад 2:

Спростити тригонометричний вираз таким чином, щоб в результаті отримати добуток тригонометричних функцій:

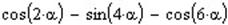
Для початку потрібно звести функції, що входять до даного виразу до функцій з однаковим аргументом (2α). Для цього використаємо оператор Simplify.

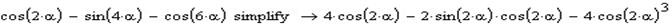
Наступним етапом буде розкладення на множники:

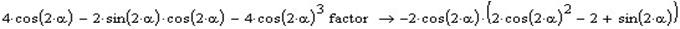
Виконаємо спрощення виразу в дужках. Для цього потрібно замінити косинус на синус, а потім розкласти на множники.

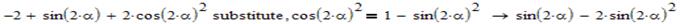
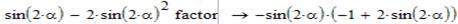
Суміщаємо першу частину, яку ми лишили – ((-2*cos(2α))) з другою, яку ми щойно спростили. Виконаємо загальне спрощення:

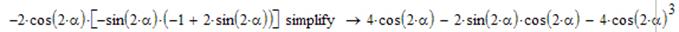
Знаємо, що 2sin2α*cos2α=sin4α, виконаємо заміну:

І виконаємо подальше розв’язання:

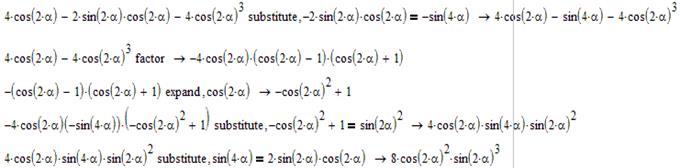
Звернемо увагу на те, що процес спрощення відбувається громіздко і важко. Простіше розв’язати особисто на папері. Те, що ми з вами повинні вивчити – ми розібрали. Вибір – користуватися спрощенням в MathCad чи ні – за вами.

Переглядів: 1764