Прості форми кристалів та їх комбінації

Кожен кристал, як було зазначено вище, характеризується цілком визначеним комплексом елементів симетрії (табл. 1.3): 32 класи, 7 сингоній, 3 категорії.

Габітус (зовнішня форма) кристалу– сукупність всіх граней, яку можна поділити на сукупності граней що симетрично рівні між собою.

В залежності від розмірів по трьох головних осях розрізняють такі обриси: ізометричний (коли всі три розміри близькі), видовжений (кристал розвинутий в одному напрямі), сплощений.

Проста форма — це сукупність граней кристалу, пов’язаних між собою елементами симетрії. Грані кожної окремої простої форми кристалів хімічних речовин є однаковими за фізичними і хімічними властивостями, а в ідеальних кристалах - і за обрисами та розмірами.

Чим більше елементів симетрії у виді (класі) симетрії, тим складніші прості форми, що властиві кристалу.

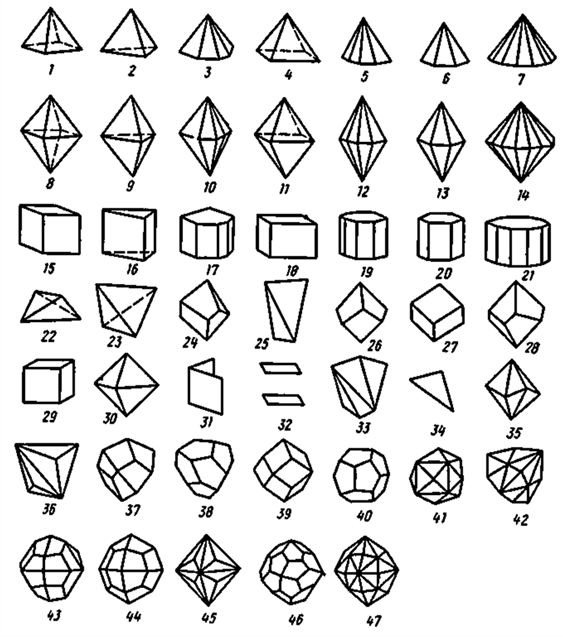
Загальна кількість простих форм – 47 (рис. 1.8).

Розрізняють загальні і власні прості форми.

Загальна проста форма - грані розміщені косо щодо усіх осей і площин симетрії.

Власна проста форма - грані або перпендикулярні хоча б до однієї осі чи площини симетрії, або паралельні до неї, або розміщені симетрично щодо двох чи декількох однакових осей або площин симетрії.

Рисунок 1.8 – Прості форми кристалів

Комбінацією простих формкристалів називається сукупність двох або кількох простих форм, об’єднаних елементами симетрії, якщо кристал утворений декількома видами граней.

На сьогоднішній день кількісний порядок вивчених кристалів становить показник ~ 10⁴. При цьому, число типів граней, за даними сучасних досліджень, може бути призведеним до значення 47 – рисунок 1.8.

Прості форми відкриті – сукупність граней не замикає простір. У якості прикладів відкритих простих форм на рисунку 1.8 представлені: а … ж, 34 – моноедр, 31 – діедр, 32 – пінакоїд.

Прості відкриті форми існують в кристалі тільки в поєднанні з іншими простими формами, формуючи комбінації простих форм.

Прості форми замкнені –простір замкнуто.

На рисунку 1.8 представлені:

1 – ромбічна піраміда, 2 – тригональна піраміда, 3 – дітригональна піраміда, 4 – тетрагональна піраміда, 5 – дітетрагональна піраміда, 6 – гексагональна піраміда, 7 – дігексагональна піраміда, 8 – ромбічна діпіраміда, 9 – тригональна діпіраміда, 10 – дітригональна діпіраміда, 11 – тетрагональна діпіраміда, 12 – дітетрагональна діпіраміда, 13 – гексагональна діпіраміда, 14 – дігексагональна діпіраміда, 15 – ромбічна призма, 16 – тригональна призма, 17 – дітригональна призма, 18 – тетрагональна призма, 19 – дітетрагональна призма, 20 – гексагональна призма, 21 – дігексагональна призма, 22 – ромбічний тетраедр, 23 – тетраедр, 24 – тригональний трапецоедр, 25 – тетрагональний тетраедр, 26 – тетрагональний трапецоедр, 27 – ромбоедр, 28 – гексагональний трапецоедр, 29 – куб, 30 – октаедр, 31 – діедр, 32 – пінакоїд, 33 – тетрагональний скаленоедр, 34 – моноедр, 35 – дітригональний скаленоедр, 36 - тригонтритетраедр, 37 – тетрагон-тритетраедр, 38 – пентагон-тритетраедр, 39 – ромбододекаедр, 40 – пентагон-додекаедр, 41 – тетрагексаэдр, 42 – гексатетраэдр, 43 – дідодекаедр, 44 – тетрагон-триоктаедр, 45 – тригон-триоктаедр, 46 – пентагон-триоктаедр, 47 – гексаоктаэдр,

Число граней залежить від виду простої форми: 1 – моноедр (рис. 1.8 № 34) … 48 – гексаоктаэдр (рис. 1.8 № 47).

Піраміди – (1 – 7) рівні трикутні грані, що перетинаються в одній точці.

Діпіраміди – (8 – 14) дві піраміди, складені своїми основами.

Призми – (15 – 21) чотирикутні грані, пересічні по паралельним ребрам.

По формі поперечного перерізу призми, піраміди і діпирамиди поділяють на: ромбічні, тригональні, дітригональні, тетрагональні, дітетрагональні, гексагональні, дігексогональні (рис. 1.8 а … ж).

Дітригональні, дітетрагональні та дігексагональні призми, піраміди та діпіраміди утворюються із відповідних простих форм шляхом здвоєння їх сторін. Такі прості форми в поперечному перерізі дають багатокутники з кутами, які повторюються через один.

Ромбічні призми мають в поперечному перерізі форму ромба та можуть бути похилими. Кут між ребрами і поперечним перерізом ≠ 90°.

Трапецоедри (рис. 1.8 №26; №28) утворені чотирикутними гранями та можуть бути представлені як повернуті навколо вертикальної вісі на деякий кут половини відповідної діпіраміди.

Скаленоедри (рис.1.8 №33, №35) утворені гранями, що мають форму нерівносторонніх трикутників.

Ромбоедр (рис. 1.8 №27) – шість граней у вигляді ромбу. Фактично це витягнутий або стиснутий за однією з вісей куб.

Тетраедр (рис. 1.8 №№22 – 25) – чотири непаралельні трикутні грані. За типом трикутної грані – кубічний тетраедр (рівносторонні трикутники), тетрагональний тетраедр (рівнобедрені трикутники), ромбічний тетраедр (трикутники зі скошеними кутами).

Куб (рис.1.8 №29) – проста форма вищої категорії (табл. 1.3).

Тобто, при наявності розглянутих 47 простих форм (рис. 1.8) їх комбінацій у природних кристалах безліч.

Напівправильні форми багатогранників. Багатогранники , у яких всі багатогранні кути рівні, а грані - правильні, але правильні багатокутники різнойменні. Багатогранники такого типу називаються рівнокутно - напівправильними.

До напівправильних багатогранників відносяться антипризми, тобто призми зі зміщеними на певний кут основами.

Найбільш простими напівправильними багатогранниками є просторові тіла з кутами багатогранника які усічені площинами іншої симетрії – усічений тетраедр, усічений октаедр, усічений ікосаедр та інш.

Зірчасті багатогранники – це багатогранники, які можуть бути одержані шляхом продовження граней вихідного багатогранника через ребра до їх наступного перетину з іншими гранями по новим ребрам.

<== попередня сторінка	\|	наступна сторінка ==>
Кристалографічні категорії, сингонії	\|

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.006 сек.