Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Потоки Субстанції

Поняття потоку й щільності потоку субстанції є фундаментальними для всієї теорії переносів. Основні вираження для них можна одержати застосовуючи "метод контрольного обсягу".

Розглянемо довільний обсяг простору, нерухомо пов'язаний із системою відліку в поле швидкостей 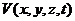загального виду, як показано на мал.2.1.

Рис.2.1.Рух субстанції через контрольний обсяг довільної форми

Кількість субстанції, що заповнювало цей обсяг у момент часу t, через проміжок часу dt займе положення, показане пунктирною лінією. Використовуючи зазначені на малюнку позначення просторових областей (А), (В), (З) і беручи до уваги, що загальна величина обсягу субстанції в процесі руху не зміниться, можна записати:

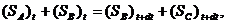(31)

або

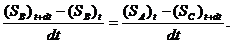(32)

У межі, коли збільшення часу спрямовується до нуля, ліва частина рівняння (32) стає швидкістю зміни субстанції в контрольному обсязі

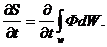(33)

Із цього випливає, що потік субстанції – це повна похідна субстанції за часом. Істотною величиною є потік щільності субстанції, дорівнює повної похідній від щільності субстанції, тобто 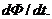Права частина рівняння (32) являє собою повний потік субстанції через контрольну поверхню. Цей потік визначається швидкістю руху субстанції й спрямований усередину контрольного обсягу на ділянці поверхні 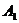і назовні на ділянці поверхні 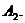Тому рівняння (32) можна записати:

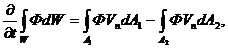(34)

де 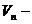компонента вектора швидкості, нормальна до поверхні контрольного обсягу; 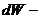елемент обсягу.

У векторній формі маємо:

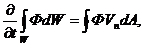(35)

де 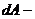вектор елемента поверхні, спрямований по внутрішній нормалі до цієї контрольної поверхні. Скалярний добуток 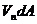позитивне для потоку, спрямованого усередину контрольного обсягу, і негативно для потоку, спрямованого назовні. Отримане вираження є загальним рівнянням нерозривності для потоку субстанції. Якщо кількість субстанції усередині контрольного обсягу постійно в часі, то рівняння (35) можна записати як

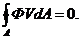(36)

Це рівняння застосовне до потоку, що встановився, субстанції.

Загальний випадок зміни субстанції пов'язаний з рухом по криволінійному шляхові з можливим локальним прискоренням і збільшенням інерційного впливу на середовище, відповідними до локальної зміни кривизни просторового шляху (кривизни відносного простору). Кривизна просторового шляху стає важливою характеристикою й може бути критерієм катастрофічних змін у середовищі субстанції, що рухається. Представимо рівняння нерозривності (29) потоку субстанції для плоского завдання в полярних координатах:

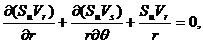(37)

де 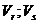- складові швидкості руху субстанції в певній крапці лінії струму по напрямках радіуса кривизни й дотичній до лінії струму в даній крапці; - збільшення радіуса кривизни і його повороту.

Для плоского потенційного потоку, що відбувається без обертання контрольного обсягу, справедливо:

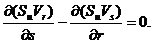(38)

У полярних координатах умова (38) запишеться у вигляді

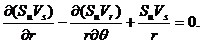(39)

У рівнянні (37) 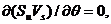а в рівнянні (39) 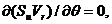тому що в першому випадку розглядається складове руху по напрямкові радіуса кривизни ділянки, а в другому – по напрямкові дотичної до лінії струму. У результаті, ці рівняння ухвалюють вид:

(40)

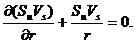(41)

Рівняння збереження імпульсу субстанції (27) для одномірного криволінійного плоского потоку (у полярних координатах) запишеться:

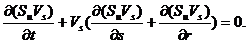(42)

У цьому рівнянні 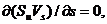тому що це рівняння є умовою сплошності (нерозривності) потоку субстанції при відсутності її припливу ззовні в досліджувану зону. Підставивши в рівняння (42) замість 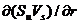рівне йому значення з (41), одержимо залежність:

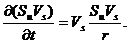(43)

Різні середовища можна представляти як ідеальні, проміжні й реальні за аналогією з рідинами: ідеальними, ньютоновськими й реальними. Ідеальні середовища це умовні середовища, у яких відсутнє внутрішнє тертя, тобто при русі немає дотичних сил тертя. Придатність моделі ідеального середовища пояснюється насамперед тим, що вона зберігає основні властивості реального середовища: її безперервність і сплошність. Крім того, модель ідеального середовища суттєво спрощує математичну постановку багатьох практично важливих завдань. Перехід від розв'язків для ідеального середовища до реальної можна здійснити внесенням виправлень на вплив в'язкості. Наприклад, перехід від розв'язків ідеальної моделі твердого тіла до реальної здійснюється як показано в третьому розділі, множенням шуканих збільшень параметрів напружено-деформованого стану на величину коефіцієнта, рівну двом.

Доцент кафедри ОПтаТЕБ к.т.н., с.н.с. В.М. Стрілець

<== попередня сторінка	\|	наступна сторінка ==>
Фізичні передумови єдиної теорії	\|	Загальне визначення технічних систем (ТС)

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.006 сек.