• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

У двовимірні та навпаки

Для формування матриці з елементів одновимірного масиву необхідно, по-перше, знати розміри створюваної матриці, по-друге, кількість елементів вхідного масиву повинна бути достатньою.

Нехай маємо масив X(16). З нього можна створити матриці A(4,4) або B(2,8) (рис. 8.2).

Рис. 2 Створення матриць

Очевидно, що протилежне перетворення буде відрізнятися тільки присвоєнням: X_L=A_i,j або X_L=B_i,j.

Розглянемо питання визначення розміру квадратної матриці.

Нехай з елементів вихідного масиву X(93) необхідно створити квадратну матрицю максимально можливого розміру. Простим підбором можна визначити, що розмір найбільшої матриці — 9х9. В загальному випадку розмір найбільшої квадратної матриці визначається як N=[ 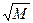], де M — розмір вихідного одновимірного масиву. В наведеному прикладі N=[ 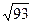]=[9,64]=9.

Приклад 5.Здано масиви A(N), B(M,N). Із додатних елементів заданих масивів створити квадратну матрицю D(X,X), де X >=2. Значення X вибрати таким, щоб масив D мав максимально можливі розміри.

Розв’язання. Алгоритм розіб’ємо на дві частини. Спочатку з додатних елементів заданих масивів сформуємо проміжний одновимірний масив С. Використовуючи проміжний масив, визначимо розміри створюваної квадратної матриці та сформуємо її. Ввід вхідних масивів та формування проміжного масиву виконується в одному циклі; L — індекс масиву С.

#include<stdio.h>

#include<math.h>

main()

{

float a[100];

float b[100][100];

int n,m,i,j,l,p,k;

double x;

printf(“Введіть кількість елементів масиву а та кількісь рядків масиву b”);

scanf(“%d%d”,&n,&m);

/*Ввід масиву*/

for(i=0;i<n;i++) scanf(“%g”,&a[i]);}

p=n+m*n;

float c[p];

l=0;

for(i=0;i<n;i++)

{

if(a[i]>0){l++;c[l]=a[i];}

}

for(i=0;i<m;i++)

{

for(j=0;j<n;j++) scanf(“%g”,&b[i][j]);

}

x=floor(sqrt(l));

if(x<2){printf(“\n””Масив створити неможливо”);goto m1;}

k=0;

float d[x][x];

for(i=0;i<x;i++)

{

for(j=0;j<x;j++)

{

k++;d[i][j]=c[k];printf(“%g”,d[i][j]);

}

print(“\n”);

}

m1:printf(“\n””Роботу закінчено”);

}

Контрольні питання

1. Що таке двовимірний масив ? Як він оголошується в програмі?

2. Особливості вводу двовимірних масивів.

3. Особливості вибору з двовимірного масиву парних(непарних) елементів.

4. Особливості перетворення одновимірних масивів в двовимірні.

Переглядів: 1001