
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Теоретичні відомості
Значна частина економічних явищ, таких як попит на товари та послуги, пасажиропотоки, виробництво в цукровій та консервній промисловості носить сезонний характер.
Для аналізу та прогнозування таких сезонних явищ використовують ряд Фур’є, який представляє сезонне явище у вигляді гармоніки.
У загальному вигляді ряд Фур’є можна записати так:
|
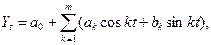
де a0, ak, bk – параметри моделі,
t – фактор часу,
k – порядковий номер гармоніки,
m – кількість гармонік.
В економетричних дослідженнях кількість гармонік ряду Фур’є приймають не більшою 4, а потім визначають, яка із гармонік найбільш адекватно описує сезонні коливання економічних явищ.
Параметри ряду Фур’є 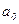 ,
, 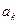 ,
, 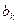 визначають методом найменших квадратів. Формули для розрахунку цих параметрів мають вигляд:
визначають методом найменших квадратів. Формули для розрахунку цих параметрів мають вигляд:
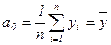 , (8.2)
, (8.2)
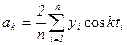 , (8.3)
, (8.3)
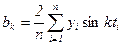 . (8.4)
. (8.4)
де n – кількість періодів часу, за які розглядається явище (місяців, днів, кварталів, років).
Для побудови економетричної моделі необхідно зробити перехід для фактора часу від натурального масштабу до радіанного або градусного. Цей перехід можна здійснити за формулою:
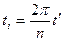 , (8.5)
, (8.5)
де n – кількість спостережень (або кількість інтервалів часу, за який аналізується сезонне явище), ti – фактор часу у радіанному (градусному) вираженні, t’ – натуральний ряд чисел від 0 до n-1 (0,1,2, …, n-1).
Запишемо місяці у радіанній формі (таблиця 8.1).
Таблиця 8.1 - Радіанна форма місяців
| Січень | Липень | 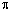
| ||
| Лютий | 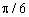
| Серпень | 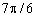
| |
| Березень | 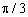
| Вересень | 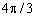
| |
| Квітень | 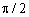
| Жовтень | 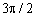
| |
| Травень | 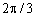
| Листопад | 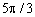
| |
| Червень | 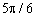
| Грудень | 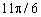
|
Для визначення параметрів моделі ak та bk необхідно скласти таблицю значень тригонометричних функцій cost, cos2t, …, sint, sin2t, … (табл. 8.2).
Таблиця 8.2 - Значення тригонометричних функцій
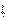
| ti, рад. | costi | cos2ti | sinti | sin2ti |
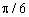
| 0,866 | 0,5 | 0,5 | 0,866 | |
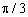
| 0,5 | -0,5 | 0,866 | 0,866 | |
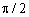
| -1 | ||||
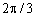
| -0,5 | -0,5 | 0,866 | -0,866 | |
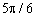
| -0,866 | 0,5 | 0,5 | -0,866 | |
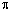
| -1 | ||||
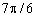
| -0,866 | 0,5 | -0,5 | 0,866 | |
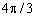
| -0,5 | -0,5 | -0,866 | 0,866 | |
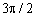
| -1 | -1 | |||
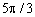
| 0,5 | -0,5 | -0,866 | -0,866 | |
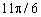
| 0,866 | 0,5 | -0,5 | -0,866 |
Для оцінювання якості прогнозу використовують показники, наведені у розрахунковій роботі № 7.
Питання для самоперевірки
1 Які економічні явища описуються за допомогою рядів Фур’є?
2 Який вигляд має ряд Фур’є?
3 Яким чином розраховують параметри ряду Фур’є?
4 Яким чином переходять від натурального масштабу до радіанного або градусного?
5 На основі якого критерію оцінують адекватність гармоніки?
| <== попередня сторінка | | | наступна сторінка ==> |
| Тестові завдання | | | Тестові завдання |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |