• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Определение главных напряжений и главных площадок

Если РїРѕ граням выделенного элементарного параллелепипеда действуют РѕРґРЅРё только нормальные напряжения, то РѕРЅРё называются главными напряжениями, Р° площадки, РЅР° которых РѕРЅРё действуют, называются главными площадками. Можно доказать, что РІ каждой точке напряженного тела существуют три главные взаимно перпендикулярные площадки (СЂРёСЃСѓРЅРѕРє3.6.). Главные напряжения обозначают s₁, s₂, s₃. РџСЂРё этом большее (СЃ учетом знака) главное напряжение обозначается s₁, Р° меньшее (СЃ учетом знака) обозначается s₃. Различные РІРёРґС‹ напряженного состояния классифицируются РІ зависимости РѕС‚ числа возникающих главных напряжений. Если отличны РѕС‚ нуля РІСЃРµ три главных напряжения, то напряженное состояние называется трехосным или объемным (СЂРёСЃСѓРЅРѕРє 3.6). Если равно нулю РѕРґРЅРѕ РёР· главных напряжений, то напряженное состояние называется двухосным илиплоским. Если равны нулю РґРІР° главных напряжения, то напряженное состояние называется одноосным или линейным.

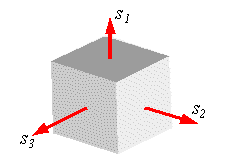
РРёСЃСѓРЅРѕРє 3.6. Главные напряжения

Для определения главных напряжений предположим, что площадка abc (СЂРёСЃСѓРЅРѕРє 3.5) является главной площадкой. РўРѕРіРґР° РЅР° ней Р±СѓРґСѓС‚ действовать только нормальные напряжения, то есть главные напряжения Р±СѓРґСѓС‚ равны полным напряжениям p. Р’ этом случае компоненты вектора полного напряжения p₁, p₂, p₃ можно рассматривать как проекции главных напряжений РЅР° РѕСЃРё координат:

.

(3.15)

Подставив это условие в уравнение (3.9), получим

.

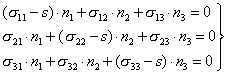(3.16)

Эти уравнения можно рассматривать как систему линейных однородных уравнений относительно направляющих косинусов. В силу известного соотношения:

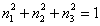
(3.17)

направляющие косинусы не могут одновременно иметь нулевые значения. В этом случае определитель, составленный из коэффициентов системы (3.16) должен быть равен нулю:

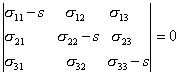
(3.18)

Раскрыв определитель, получим характеристическое уравнение третьего РїРѕСЂСЏРґРєР°:

,

(3.19)

где коэффициенты

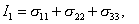
	(3.20)
,	(3.21)
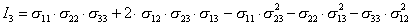
	(3.22)

называются инвариантами напряженного состояния в точке, так как они не изменяют своей величины при изменении направления исходной системы прямоугольных координат. Можно доказать существование трех действительных корней уравнения (3.19). На основании этого можно считать, что в каждой точке тела, независимо от его формы и размеров, места приложения, вида и характера нагрузок, существует не более трех взаимно ортогональных главных напряжения.

Для определения положения главных площадок необходимо знать направляющие косинусы нормали к этой площадке. Для их определения следует воспользоваться системой уравнений (3.16). Однако равенство нулю определителя этой системы указывает на то, что не все уравнения системы являются линейно независимыми; одно из них есть следствие двух других. Чтобы сделать систему определенной, надо добавить к ней равенство (3.17). После этого число независимых уравнений становится достаточным для однозначного определения направляющих косинусов.

Читайте також:

1. Определение механических свойств материала при растяжении

Переглядів: 830