
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Періодичні функції та їх властивості
Означення: Функція 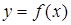 , задана на множині
, задана на множині 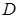 , називається періодичною, якщо існує таке число
, називається періодичною, якщо існує таке число  , що
, що
1. 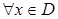
 і
і 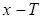 також належить
також належить 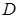 ,
,
2. 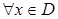
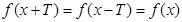
Приклад 1 : 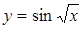 не є періодичною , бо
не є періодичною , бо  обмежена
обмежена  ‒ не виконується умова 1.
‒ не виконується умова 1.
Приклад2 : Чи є функція  періодичною.
періодичною.  повинно виконуватись:
повинно виконуватись:  , тобто
, тобто  ,
,  , якщо
, якщо 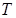 ‒ період, то
‒ період, то  повинна виконуватись ця рівність. Таке
повинна виконуватись ця рівність. Таке 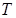 не існує. Наприклад , при
не існує. Наприклад , при  , що суперечить умові.
, що суперечить умові.
Щоб встановити неперіодичність функції, досить показати, що вона не періодично повторює хоча б одну властивість (нулі, проміжки монотонності і так далі). Так, наприклад, функція  не є періодичною, оскільки вона має тільки один нуль, що неможливо для періодичної функції.
не є періодичною, оскільки вона має тільки один нуль, що неможливо для періодичної функції.
Приклад: Оскільки синус і косинус визначені на усій числовій прямій і  для будь-кого
для будь-кого 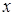 , синус і косинус ‒ періодичні функції з періодом
, синус і косинус ‒ періодичні функції з періодом 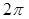 .
.
Теорема: Якщо  і
і  є періодами функції
є періодами функції  , то їх сума
, то їх сума  також є періодом функції
також є періодом функції  .
.
Доведення.
Нехай  і
і  ‒ періоди функції
‒ періоди функції 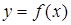 , тоді
, тоді


Покажемо, що  ‒ період функції
‒ період функції 

 що і треба було довести.
що і треба було довести.
Наслідок: Якщо функція  періодична з періодом
періодична з періодом 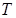 , то при будь-якому цілому
, то при будь-якому цілому  число
число  теж період цієї функції.
теж період цієї функції.
Якщо функція періодична, то періодів нескінченно багато. Найменший додатний період називатиме основним (головним) періодом функції.
Найменший додатний період функцій  і
і 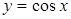 рівний
рівний 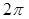 .
.
Найменший додатний період функцій 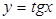 і
і  рівний
рівний  .
.
Доведемо твердження для функції  .
.
Той факт, що для функції  число
число 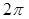 є періодом витікає безпосередньо із означення.
є періодом витікає безпосередньо із означення.
Доведемо, що цей період є найменшим додатним методом від супротивного. Припустимо, що існує таке число Т< 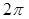 , що є періодом функції
, що є періодом функції  . Це означає, що для всіх дійсних х виконується умова
. Це означає, що для всіх дійсних х виконується умова  . Отже дана умова виконується також і для
. Отже дана умова виконується також і для  ,
,  ;
;
 звідси
звідси 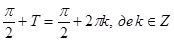 ;
;
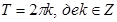 і
і  . А це означає, що
. А це означає, що  ‒ ціле число. Отримана суперечність свідчить про невірність припущення про існування періоду меншого за
‒ ціле число. Отримана суперечність свідчить про невірність припущення про існування періоду меншого за 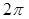 .
.
Теорема. Якщо періодична функція має основний період 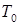 , то будь-який інший її період буде кратним,
, то будь-який інший її період буде кратним, 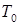 , тобто
, тобто  , де
, де  .
.
Доведення (від супротивного)
Нехай існує такий період 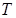 , функції
, функції  , що
, що  не є цілим числом, тоді,
не є цілим числом, тоді,  , де
, де  ,
,  . Але
. Але 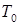 і
і  - періоди функції
- періоди функції  і тому
і тому  числа
числа  й
й 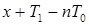 належить
належить  і
і 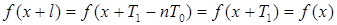 .
.
Тобто число  <
< 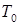 , є періодом функції
, є періодом функції  . Це суперечить припущенню, що
. Це суперечить припущенню, що 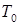 ‒ найменший додатний період функції
‒ найменший додатний період функції  . Отже, припущення невірне, тобто
. Отже, припущення невірне, тобто  ‒ ціле число.
‒ ціле число.
Приклад: Доведемо, що функція  періодична і її найменший додатний період рівний
періодична і її найменший додатний період рівний 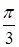 .
.
Катангенс визначений при усіх значеннях аргументу, не рівних  . Тому область визначення цієї функції складається з таких
. Тому область визначення цієї функції складається з таких 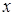 , що
, що
 , тобто
, тобто  .
.
Звідси слідує , що  разом з довільним
разом з довільним 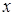 містить і усі точки виду
містить і усі точки виду
 . Очевидно
. Очевидно 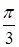 є періодом функції
є періодом функції 
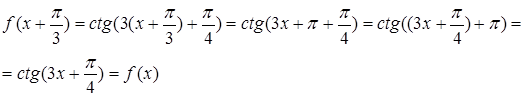 .
.
Залишається довести, що число 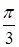 ‒ найменший додатний період
‒ найменший додатний період  . Припустимо, що періодом
. Припустимо, що періодом  є таке число
є таке число  , що
, що  . Тоді
. Тоді  справедлива рівність
справедлива рівність

оскільки 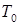 ‒ період функції. Але це означає, що
‒ період функції. Але це означає, що  . Але
. Але  ‒ найменший додатний період функції
‒ найменший додатний період функції 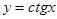 , пришли до суперечності.
, пришли до суперечності.
Справедливе також твердження:
Якщо функція  періодична і має період
періодична і має період 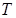 , то функція
, то функція  , де
, де  ‒ сталі, і
‒ сталі, і 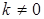 , також періодична, причому її період рівний
, також періодична, причому її період рівний  .
.
З цього твердження слідує, що для функцій  . Для функцій
. Для функцій  .
.
Проте функція, яка є алгебраїчною сумою, добутком, часткою 2-х або декількох функцій з різними періодами, може виявитися і неперіодичною.
Наприклад: функції 
 ‒ періодичні, якщо число
‒ періодичні, якщо число  є раціональним числом, і неперіодичною, якщо
є раціональним числом, і неперіодичною, якщо  ‒ ірраціональне число.
‒ ірраціональне число.
Так, функція  ‒ періодична, оскільки
‒ періодична, оскільки  ‒ раціональне число
‒ раціональне число 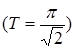 , а функція
, а функція  ‒ неперіодична, оскільки
‒ неперіодична, оскільки  ‒ ірраціональне число.
‒ ірраціональне число.
Період функції.
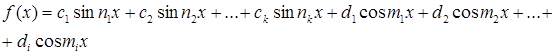
де сума 2-х чи декількох членів ряду тотожно не дорівнює нулю
 і відмінні від нуля,
і відмінні від нуля,  .
.
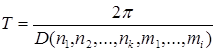 , де
, де 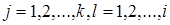 .
.
Аналогічно, період функції
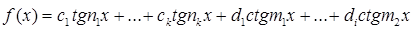 знайдемо за формулою
знайдемо за формулою  .
.
Якщо 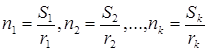
 , де
, де  , то період функції рівний
, то період функції рівний 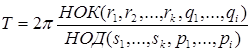 ; а період функції за формулою:
; а період функції за формулою:  .
.
Наприклад :  ;
;
 .
.
Переглядів: 5549