- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Закон Стефана Больцмана. Закон Віна.
У 1884 р. Л. Больцман, застосувавши термодинамічний метод для дослідження рівноважного теплового випромінювання всередині замкненої порожнини, теоретично показав, що: інтегральна випромінювальна здатність абсолютно чорного тіла пропорційна до четвертого степеня його абсолютної температури:
. (3.6)
Цей закон називають законом Стефана–Больцмана. Коефіцієнт пропорційності 
–стала Стефана-Больцмана. Внаслідок численних експериментів знайдено, що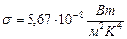 
.
Енергія, яка випромінюється за час t абсолютно чорним тілом з поверхні S при температурі Т, дорівнює:
. (3.7)
Якщо абсолютне чорне тіло оточене середовищем, яке має температуру 
, то таке тіло буде поглинати енергію, що випромінюється середовищем. В цьому випадку різниця між енергіями, що випромінюється і поглинається абсолютно чорним тілом приблизно виражається формулою:
. (3.8)
До реальних тіл закон Стефана-Больцмана не застосовний, оскільки спостереження показують більш складну залежність 
від температури, а також від форми тіла і стану його поверхні.
Використовуючи закони термодинаміки і електродинаміки, В.Він у 1893 р. встановив характер залежності випромінювальної здатності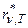 
абсолютно чорного тіла від частоти і температури:
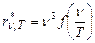, (3.9)
де 
– функція, яка виражає відношення частоти випромінювання абсолютно чорного тіла до його температури.
Із закону Віна можна знайти залежність частоти 
, що відповідає максимальному значенню випромінювальної здатності 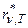абсолютно чорного тіла, від температури Т. А саме
, (3.10)
де 
– стала величина – стала Віна.
Рівняння 
виражає закон зміщення Віна: частота, яка відповідає максимальному значенню випромінювальної здатності 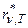абсолютно чорного тіла, прямо пропорційна до його абсолютної температури.
Закон зміщення Віна можна записати в дещо іншій формі, розглядаючи максимум випромінювальної здатності абсолютно чорного тіла 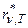, віднесеної до інтервалу 
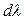довжин хвиль (у вакуумі): довжина хвилі 
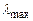, яка відповідає максимальному значенню випромінювальної здатності 
абсолютно чорного тіла, обернено пропорційна до його температури:
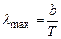, (3.11)
де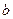 
– стала Віна, 
.
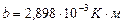Із закону Віна видно, що при зниженні температури абсолютно чорного тіла максимум енергії його випромінювання зміщується в область більших довжин хвиль.
Значення максимуму випромінювальної здатності абсолютно чорного тіла пропорційне до п’ятого степеня його абсолютної температури:
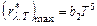, (3.12)
де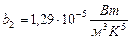 
.
Квантова гіпотеза. Формула Планка
В 1900 р. М.Планк вперше знайшов правильний вираз для функції Кірхгофа і обґрунтував спектральні закономірності випромінювання абсолютно чорного тіла.
В своїх розрахунках Планк вибрав найпростішу модель випромінювальної системи у вигляді сукупності лінійних гармонічних осциляторів (електричних диполів) з найрізноманітнішими частотами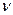 
. Як показав Планк, випромінювальна здатність абсолютно чорного тіла
,
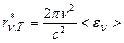де 
– середнє значення енергії осцилятора з власною частотою .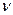
Правильний вираз для середньої енергії осцилятора 
, а, отже, і функції Кірхгофа вдалось знайти Планку введенням квантової гіпотези, яка зовсім не притаманна класичній фізиці. У класичній фізиці припускається, що енергія будь-якої системи може змінюватись неперервно, набираючи будь-яких, як завгодно близьких значень.
За квантовою гіпотезою Планка енергія 
осцилятора може набувати тільки певних дискретних значень, які дорівнюють цілому числу елементарних порцій – квантів енергії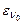 
:
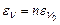
. (3.13)
Тобто, згідно з гіпотезою Планка атоми і молекули випромінюють енергію окремими порціями, або квантами, величина яких 
( 
).
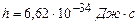Вираз для Планк отримав в такому вигляді:
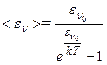. Тому формула Планка для випромінювальної здатності абсолютно чорного тіла має вигляд:
, або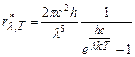 
. (3.14)
Переглядів: 2155