
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Термодинамічна модель процесу перед руйнування у металевих конструкціях, що перебувають під дією статичних навантажень
РОЗДІЛ 2
ВДОСКОНАЛЕННЯ МЕТОДУ КОНТРОЛЮ ПЕРЕДДЕФЕКТНОГО СТАНУ МЕТАЛЕВИХ КОНСТРУКЦІЙ, ЩО ПЕРЕБУВАЮТЬ ПІД ДІЄЮ СТАТИЧНИХ НАВАНТАЖЕНЬ
Термодинамічна модель процесу перед руйнування у металевих конструкціях, що перебувають під дією статичних навантажень
Передача тепла може відбуватися трьома способами: теплопровідністю, конвекцією і випромінюванням. У нашому випадку процес передачі тепла відбувається за допомогою теплопровідності, шляхом безпосереднього дотику частинок неоднорідної структури металу з різною температурою.
Теплопровідність представляє собою, згідно з поглядами сучасної фізики, молекулярний процес передачі тепла. Передача тепла теплопровідністю залежить від фізичних властивостей тіла, його геометричних розмірів [70].
В загальному випадку процес передачі тепла теплопровідністю в твердому тілі супроводжується зміною температури Т як у просторі, так і в часі [71]:
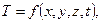
| (2.1) |
де 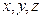 - просторові координати точки;
- просторові координати точки;  - час.
- час.
Ця функція визначає температурне поле в однорідному ізотропному тілі. Під температурним полем будемо розуміти сукупність значень температури в даний момент часу для всіх точок досліджуваного простору, в якому протікає процес.
Границя відношення зміни температури 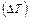 до відстані між ізотермічними поверхнями по вектору нормалі
до відстані між ізотермічними поверхнями по вектору нормалі 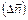 , яка прямує до нуля, називають градієнтом температури, який у загальному випадку розраховується за формулою [72]:
, яка прямує до нуля, називають градієнтом температури, який у загальному випадку розраховується за формулою [72]:
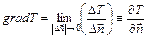 , ,
| (2.2) |
Градієнт температури – це вектор, напрямлений по нормалі до ізотермічної поверхні в сторону збільшення температури і чисельно рівний частковій похідній від температури у цьому ж напрямку [73].
Для поширення тепла в будь-якому тілі необхідною умовою є наявність різниці температур в різних точках тіла. Зв'язок між кількістю тепла 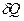 , яка проходить за проміжок часу
, яка проходить за проміжок часу 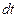 через елементарну площину
через елементарну площину 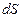 , розташовану на ізотермічній поверхні, і градієнтом температури встановлюється за допомогою гіпотези Фур'є, згідно якої [74]:
, розташовану на ізотермічній поверхні, і градієнтом температури встановлюється за допомогою гіпотези Фур'є, згідно якої [74]:
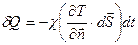 , ,
| (2.3) |
де 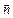 - це вектор нормалі до елемента поверхні dS.
- це вектор нормалі до елемента поверхні dS.
Від'ємний знак у правій частині вказує на те, що в напрямку теплового потоку температура зменшується і 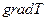 є величиною від'ємною. Коефіцієнт пропорційності
є величиною від'ємною. Коефіцієнт пропорційності 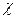 називається коефіцієнтом теплопровідності або більш коротко – теплопровідністю [75]. Під тепловим потоком
називається коефіцієнтом теплопровідності або більш коротко – теплопровідністю [75]. Під тепловим потоком 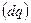 будемо розуміти відношення кількості тепла, що проходить через задану поверхню, до часу:
будемо розуміти відношення кількості тепла, що проходить через задану поверхню, до часу: 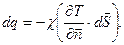
Відношення теплового потоку 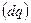 через елементарну частинку ізотермічної поверхні до елемента площі
через елементарну частинку ізотермічної поверхні до елемента площі 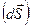 цієї поверхні називають поверхневою густиною теплового потоку
цієї поверхні називають поверхневою густиною теплового потоку 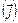 (або вектором густини теплового потоку):
(або вектором густини теплового потоку): 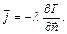 Вектори
Вектори 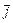 і
і 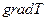 лежать на одній прямій і напрямлені у протилежні сторони [76].
лежать на одній прямій і напрямлені у протилежні сторони [76].
Тепловий потік, що проходить через довільну поверхню знаходять за допомогою виразу:
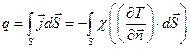 . .
| (2.4) |
Кількість тепла, що пройшла за одиницю часу через цю поверхню визначається інтегралом:
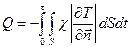 . .
| (2.5) |
Таким чином, для визначення кількості теплоти необхідно знати температурне поле всередині тіла. Знаходження температурного поля складає основну задачу аналітичної теорії теплопровідності.
Вивчення будь-якого фізичного процесу пов'язане з встановленням залежностей між величинами, які характеризуються даний процес. Зв'язок між величинами, що приймають участь в передачі тепла теплопровідністю, встановлюється диференціальним рівнянням теплопровідності [77].
Диференціальне рівняння теплопровідності з джерелом тепла всередині тіла має вигляд [78]:
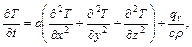
| (2.6) |
де с – питома теплоємність середовища;
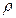 - густина середовища;
- густина середовища;
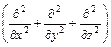 - оператор Лапласа, який позначають скорочено
- оператор Лапласа, який позначають скорочено 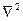 ;
;
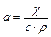 - коефіцієнт температуропровідності, що характеризує швидкість зміни температури;
- коефіцієнт температуропровідності, що характеризує швидкість зміни температури;
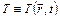 - об’ємно-часова функція розподілу температури;
- об’ємно-часова функція розподілу температури;
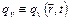 .
.
Рівняння теплопровідності можна переписати у наступному вигляді:
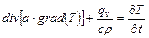 . .
| (2.7) |
Оскільки, напружено-деформований стан характеризується динамічними процесами утворення і анігіляції різного роду дефектів, то слід звернути увагу на постійну взаємодію останніх та кількість тепла, яка виділяється під час утворення мікротріщин.
Під час розрахунку кількості тепла необхідно враховувати як вплив енергії, що виділяється під час зародження мікротріщин так і вплив точкових дефектів, які утворились поблизу такої мікротріщини. Проте, якщо врахувати малі розміри точкових дефектів (~10-9 м), то для розрахунку калориметричного ефекту доцільно застосувати наступну модель теплового джерела:
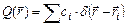
| (2.8) |
де 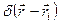 - функція Дірака [79];
- функція Дірака [79];
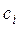 - тепловий ефект утворення мікротріщини;
- тепловий ефект утворення мікротріщини;
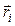 - розташування мікротріщини.
- розташування мікротріщини.
Дослідження дефектної мікроструктури металу [52] показують, що при пластичній деформації утворюються мікротріщини, поблизу яких спостерігається максимальне накопичення точкових дефектів, кількість яких зменшується в залежності від віддалі до мікротріщини. Тому, для математичних розрахунків доцільно припустити, що поширення тепла від джерела енергії можна описати за допомогою гаусівського розподілу.
Врахувавши вище наведене, рівняння для визначення джерела тепла буде мати вигляд [80]:
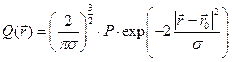 . .
| (2.9) |
де Р – потужність джерела тепла;
s – середнє квадратичне відхилення;
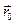 – положення джерела теплової енергії.
– положення джерела теплової енергії.
Задачею дослідження є визначення температурного розподілу на поверхні зразка у формі паралелепіпеда (рис.2.1).
Рис. 2.1. Елемент зразка з ймовірною зоною утворення мікродефекту.
Таке формулювання задачі дослідження передбачає розв’язання рівняння теплопровідності (2.7) з відповідними початковими та краєвими умовами, що дозволяє визначити температурний розподіл на поверхні зразка та сформулювати основні вимоги до системи контролю.
Переглядів: 819