- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Робота сили та її вираз через криволінійний інтеграл
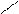Нехай тіло рухається прямолінійно і на всьому переміщенні 
на нього діє стала за величиною і напрямком сила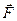 
, яка утворює кут 
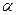з напрямком переміщення. Дію сили 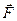на переміщенні , характеризують величиною, яку називають роботою.
Робота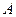 
, яка виконана силою 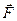, – це фізична величина, яка дорівнює скалярному добутку сили на переміщення:
,
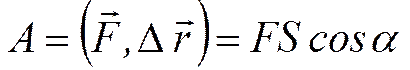де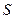 
– шлях пройдений тілом за час дії сили.
Елементарною роботою 
сили 
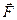на переміщенні 
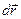називається скалярна величина
,
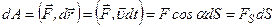де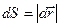 
- елементарний шлях, α – кут між векторами 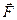і ,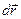 
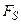- проекція вектора 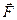на напрямок вектора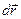
Якщо на тіло, яке рухається поступально, одночасно діють декілька сил, то робота рівнодійної сили при переміщенні на 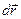дорівнює алгебраїчній сумі робіт складових сил:
.
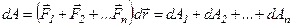Сила 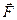, що діє на матеріальну точку або на тіло, яке рухається поступально, називається консервативною або потенціальною, якщо робота 
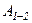, яка виконується цією силою при переміщенні точки (тіла) з одного довільного положення 1 в інше 2, не залежить від того, вздовж якої траєкторії відбулось це переміщення (рис. 9):
.
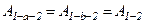Зміна напрямку руху вздовж траєкторії на протилежний спричинює зміну знака роботи (кут a замінюється на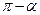 
і cos a змінює свій знак). Тому робота консервативної сили при переміщенні матеріальної точки вздовж замкненої траєкторії L (1-а-2-b-1) тотожно дорівнює нулю:
.
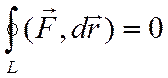Прикладами консервативних сил можуть бути сили тяжіння, гравітаційні сили, сили пружності, сили електростатичної взаємодії між зарядженими тілами.
Кінетичною енергією механічної системи називається енергія механічного руху цієї системи.
Сила 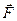, яка діє на тіло і викликає його рух, виконує роботу, а енергія рухомого тіла зростає на величину виконаної роботи:
.
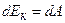Використовуючи скалярний запис другого закону Ньютона і помноживши обидві частини на елементарний шлях dS, отримаємо
.
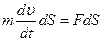Оскільки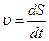 
, то
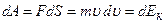
і
.
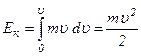співвідношення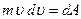 
вздовж деякої траєкторії від точки 1 до точки 2 в яких швидкість тіла 
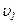і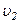 
відповідно:
.
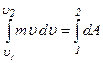Звідси,
.
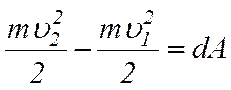Отже, зміна кінетичної енергії тіла дорівнює роботі, яка виконується над тілом.
Кінетичній енергії тіла можна надати і такого вигляду:
,
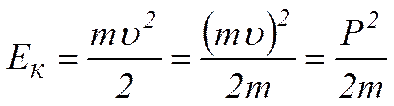де Р – імпульс тіла.
Кінетична енергія тіла не може бути від’ємною.
Повна кінетична енергія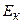 
системи дорівнює сумі кінетичних енергій 
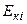всіх тіл, що входять до неї:
.
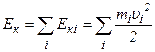Кінетична енергія системи залежить від величини мас і швидкостей руху тіл, що входять до неї. При цьому неістотно, як тіло з масою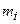 
набуло швидкості 
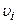. Цей висновок можна сформулювати так: кінетична енергія системи є функцією стану її руху.
Швидкість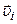 
істотно залежить від вибору системи відліку. В різних інерціальних системах відліку, що рухаються одна відносно одної, швидкість 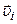і-го тіла системи, а отже, його кінетична енергія системи будуть неоднакові.
Кінетична енергія системи залежить від вибору системи відліку, тобто є величиною відносною.
Якщо в інерціальній системі відліку (і.с.в.) К кінетична енергія системи дорівнює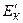 
, то в і.с.в. 
, яка рухається відносно К поступально з швидкістю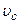 
, центра мас системи, то
,
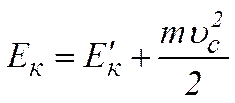де m – маса системи, 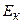- кінетична енергія системи відносно і.с.в. .
Ця рівність описує теорему Кюніга: кінетична енергія механічної системи дорівнює сумі кінетичної енергії цієї системи при її русі відносно і.с.в. , яка поступально рухається з початком в центрі мас і кінетичної енергії, яку мала би матеріальна точка, що має масу, яка дорівнює масі всієї системи і рухається зі
швидкістю її центра мас.
Переглядів: 3826