• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Закон рівномірного розподілу енергії за ступенями вільності молекул

Для того, щоб визначити енергію, яка припадає на всі рухи молекул, необхідно ввести поняття про число ступенів вільності.

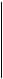Числом ступенів вільності називають найменше число координат, які необхідно задати для того, щоб повністю визначити положення тіла у просторі, або кількість незалежних рухів, які може виконувати тіло.

У класичній статистичній фізиці виводиться закон Больцмана про рівно­мірний розподіл енергій за ступенями вільності молекул:

для статистичної системи, що перебуває у стані термодинамічної рівноваги, на кожний поступальний і обертальний ступінь вільності припадає в середньому кінетична енергія, що дорівнює 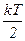, а на кожний коливальний ступінь вільності – в середньому енергія .

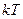Коливальний ступінь має вдвоє
більшу енергію тому, що на нього припадає не лише кінетична енергія, як у разі поступального і обертального руху, але і потенціальна енергія, причому середні зна­чення кінетичної і потенціальної енергій однакові:

.

Таким чином, середня енергія молекули

,

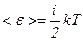де .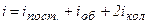

Важливою характеристикою термодинамічної системи є її внутрішня енергія

U – енергія хаотичного (теплового) руху мікрочастинок системи (молекул, атомів, електронів, ядер і тощо) і енергія взаємодії цих частинок.

В ідеальному газі немає сил взаємодії між молекулами, а, отже, дорівнює нулю взаємна потенціальна енергія молекул. Тому для моля ідеального газу внутрішня енергія дорівнює сумі кінетичних енергій молекул:

.

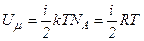Якщо є 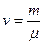молів газу, то його внутрішня енергія

.

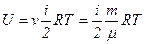Внутрішня енергія ідеального газу залежить від кількості ступенів вільності молекул і абсолютної температури газу.

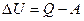, або .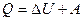

Це рівняння є математичним виразом першого закону термодинаміки:

теплота, надана системі, витрачається на збільшення її внутрішньої енергії і на виконання системою роботи проти зовнішніх сил.

Вираз для першого закону термодинаміки для нескінченно малої зміни стану системи матиме вигляд:

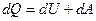
або в коректнішій формі

,

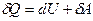де 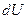– нескінченно мала зміна внутрішньої енергії системи, 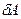– нескінченно мала робота, 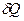– нескінченно мала кількість теплоти. У цьому виразі 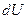є повним диференціалом, а 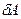і 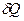не є повними диференціалами, а функціоналами і залежать від вигляду функції, що описує перехід з одного стану в другий.

Дуже важливим є випадок, коли
система – це періодично діюча машина, в якій газ, пара або інше “робоче тіло” внас­лідок деякого процесу повертається до початкового стану. У цьому раз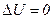і

і .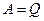

Робота, що виконується машиною за один цикл, дорівнює підведеній ззовні теплоті 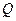. Цей висновок дає змогу сформулювати перший закон термодинаміки так:

неможливо побудувати періодично діючий двигун, який виконував би роботу без підведення енергії ззовні або виконував би роботу більшу, ніж кількість переданої йому ззовні енергії (вічний двигун першого роду неможливий).

Для характеристики теплових властивостей газу, як i будь-якого iншoгo тіла, користуються особливою величиною – теплоємністю.

Теплоємністю тіла називається фізична величина, яка числово дорівнює кількості теплоти, яку потрібно надати тілу, щоб підвищити його температуру на один кельвін:

.

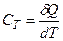Значення 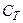залежить від маси тіла, його хімічного складу, термодинамічного стану i виду процесу зміни стану тіла, в якому надходить теплота .

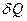Питомою теплоємністю c називається фізична величина, що числово дорівнює кількості теплоти, яку слід надати одиниці маси цієї речовини для підвищення її температури на :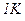

.

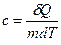Молярною теплоємністю C називається фізична величина, яка числово дорівнює кількості теплоти, яку треба надати одному молю речовини для підвищення його температури на :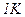

,

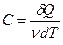де 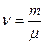– кількість молей газу.

Між молярною теплоємністю 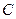і питомою теплоємністю 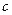існує співвідношення: .

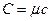Якщо нагрівають газ, то згідно з
першим законом термодинаміки

,

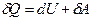а для одного моля газу

.

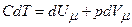Якщо газ нагрівається при сталому об’ємі, то надана газу теплота йде лише на збільшення його внутрішньої енергії:

.

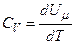Якщо газ нагрівається при сталому тиску, то

.

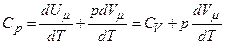Тут враховано, що 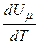не залежить від виду процесу, оскільки внутрішня енергія ідеального газу не залежить ні від 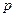, ні від 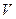, а визначається лише температурою. Тому завжди .

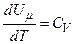Згідно з рівнянням Клапейрона-Менделєєва

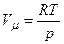і .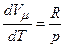

В результаті

.

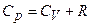Отриманий вираз називається рівнянням Майєра.

Оскільки

,

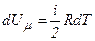то

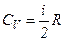і .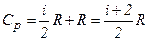

Кожний газ характеризується величиною

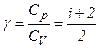і .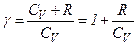

Звідси

.

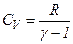Отримані вирази для 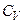і добре збігаються з експериментом для одноатомних і багатьох двоатомних газів при кімнатній температурі 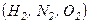. Однак у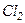 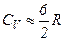, що неможливо пояснити. У триатомних газів спостерігаються систематичні відхилення від теорії.

Експеримент показав, що теплоємність залежить від температури. Водночас згідно з формулами для 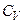і вона стала для даного газу.

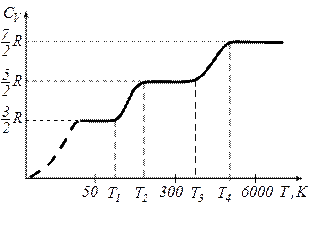
Графічно залежність теплоємності 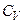водню від температури показано на рисунку. При низьких температурах до температури .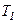

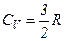Ізопроцесами в газах називаються процеси, при яких один із основних параметрів стану 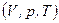зберігається сталим.

Ізохорний процес .

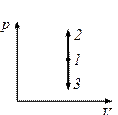Діаграма цього процесу в координатах p, V зображається прямою, яка паралельна до осі ординат, де 1-2 – ізохорне нагрівання, а 1-3 – ізохорне охолод­ження

При ізохорному процесі газ не виконує роботи над зовнішніми тілами: δA=pdV=0.

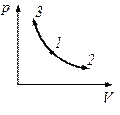Отже, з першого закону термодинаміки δQ=dU+δA для ізохорного процесу випливає, що δQ=dU. Оскільки

,

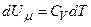то для довільної маси газу

.

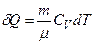Ізобарний процес .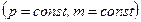

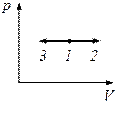Діаграма цього процесу в координатах p, V зображається прямою, яка паралельна до осі V 1-2 – ізобарний процес розширення, 1-3 – ізобарний стиск.

Робота, яку виконує газ при ізобарному розширенні від об’єму 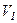до 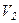, до­рівнює

,

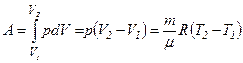де використано рівняння Клапейрона-Менделєєва.

При ізобарному процесі при наданні газу масою m кількості теплоти

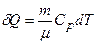
його внутрішня енергія зростає на величину

.

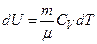Газ виконує роботу

.

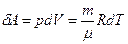Ізотермічний процес .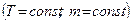

Діаграма цього процесу в координатах p, V є гіперболою. 1-3 – ізотермічний стиск, 1-2 – ізотермічне розширення

Робота газу при ізотермічному роз­ширенні:

.

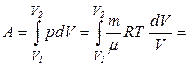
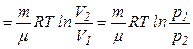При 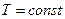внутрішня енергія ідеального газу не змінюється, тобто

і ,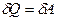

тобто вся кількість теплоти, надана газу, витрачається на виконання ним роботи проти зовнішніх сил:

.

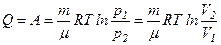Робота розширення газу 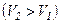додатна. У випадку стиску газу (процес 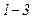) робота A, що виконується газом, від’ємна, водночас зовнішні сили виконують додатну роботу 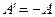. При цьому 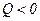, тобто теплота від газу відводиться.

Переглядів: 3099

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове.