Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Розвиток уявлень про число та лічбу у дітей дошкільного віку

Основні поняття: аксіома лічби, числівники, рівнопотужні множини, взаємнооднозначна відповідність, образ числа, цифра, натуральний ряд чисел, розвиток уявлень про число і лічбу у різних вікових групах, склад числа.

Прийняття Базового компонента дошкільної освіти та вимога обов’язкової логіко-математичної підготовки дітей до школи змінюють чинні підходи до організації навчання математики у ДНЗ. Формалізований характер математичних знань вимагають більш продуманих інноваційних підходів, котрі створювали б особистісно-сприятливе навчальне середовище. Однак поряд із засвоєнням змісту предмета необхідно закладати у дошкільнят основи операційного мислення.

Аналіз стану викладання математики у ДНЗ показує, що акцент робиться на змісті, логіці його викладу, систематизації, методичному забезпеченні процесу передачі знань від дорослого до дитини. Домінування у навчальній діяльності дошкільнят репродуктивних форм її організації, недооцінка вироблення операційних компонентів мислення на різнотипних завданнях програмує формування навчальних стереотипів.

Під операційним розуміємо мислення, яке передбачає виконання розумових дій, пов’язаних з перетворенням предметів, явищ дійсності. Операційність є здатність мозку відтворювати акти перетворення, зміни навколишньої дійсності і повторювати, копіювати їх у мисленні дитиною. Попередній досвід спостереження за змінами у природі, побуті, соціальному середовищі дозволяє дитині з часом самостійно у мисленнєвому, внутрішньому плані здійснювати розумові операції, а пізніше і планувати їх виконання. А це і є джерелом змін усередині самої дитини, що може забезпечити їй певну автономію у саморозвитку і самовизначенні, може позитивно відбитися на процесах соціалізації особистості школяра надалі.

Кількісна лічба передує у часі порядковій і здійснюється у певній послідовності: 1) перелічування предметів, що мають однакові властивості (форму, величину, колір), 2) лічба предметів, що відрізняються однією ознакою (великі – маленькі, високі – низькі, товщі – тонші); 3) рахування предметів, розміщених лінійно (у рядок чи колонку), тобто мають початок відліку; 4) визначення чисельності множини, коли предмети мають довільне просторове розташування на площині малюнка; 5) початок відліку не задається, предмети розміщені по кільцевому принципу і дитина має вибрати перший для лічби предмет і зафіксувати його; 6) практичні дії з роздавальним матеріалом, коли дитина будує серіаційні ряди за вказівкою вчителя чи самостійно вибирає спосіб лічби предметів, співвідносить із числовими фігурами, почергово викладає на столі та називає число.

Правомірність такої системи завдань у навчанні математики дошкільників полягає у поєднанні форми мислення з просторовим образом числа, навчанням математики на основі альтернативних варіантів просторового представлення чисельності множин. Такі завдання дозволяють формувати поняття натурального числа на різнотипних завданнях при збереженні істотних, суттєвих інваріантних кількісних характеристик множини. Для закріплення навичок лічби дітям пропонуються завдання на відлік певної кількості предметів за зразком (цифрою), на встановлення незалежності чисельності множини від величини, форми предметів, їх розміщення та відстані між ними.

Операційнісгь важливо враховувати якраз на п’ятому році життя, бо в цей період інтенсивно розвивається орієнтовно-дослідницький рефлекс дитини. І тому необхідно дати їй можливість самореалізації в навчальних ситуаціях, у яких вона поставлена перед вільним вибором власного способу виконання завдання. Наприклад, на малюнку лісового пейзажу зображені тварини. Діти розповідають про те, де які тварини знаходяться і відповідають на запитання: “Чому сховався зайчик? Від кого він сховався? Скільки зайчиків? Де вони ховаються? Де знаходиться лисичка?”. Після цього дітям пропонується прикласти малюнок ще одного зайчика так, щоб його не побачила лисичка.

Ознайомлення із математичними відношеннями в межах перших п’яти чисел відбувається у практичних діях на прикладання, накладання предметів чи їх оптичний аналіз.

Для закріплення поняття кількісної лічби можна запропонувати гру “Доміно”. До комплекту входять по два набори, у кожному із яких по 5 (10) карток. Набори відрізняються між собою тим, що у першому із них зображені предмети рослинного чи тваринного світу, а у другому – є зображення цифр. „Доміно” належить до ігор з правилами, в яких одночасно беруть участь двоє гравців, тобто передбачається парна робота. Перший варіант “Доміно” можна використовувати для закріплення поняття рівнопотужних множин, а другий – складу чисел у межах 5 (10).

Розглянемо послідовність ознайомлення дітей дошкільного віку з лічбою.

У ранньому віці у дошкільників формуються навички оперування з множинами: утворення множин, усвідомлення принципу кількісного порівняння чисельності двох множин, використання термінів для порівняння множин за певними ознаками. У предметно-практичній роботі з множинами у дітей формується м’язо-зоровий-руховий образ числа. Спостереження за навколишнім середовищем, спілкування з дорослими, участь у побутових ситуаціях сприяють накопичення пізнавального досвіду щодо чисельності множин. Операційність на цьому етапі лічильної діяльності полягає у відтворення, наслідуванні зразків соціальної поведінки дорослих, намаганні повторювати слова-терміни, які вони чують від інших, повторювати дії старших. Пізнавальний пошук дітей раннього віку зосереджений на вивченні предметного світу в цілому, а не окремих його складових. Лічба предметів на цьому етапі розвитку дітей носить формальний характер, оскільки забезпечує природну допитливість дитини інформацією про математичний бік дійсності. Оперування з дискретними множинами дозволяє порівнювати чисельності множин без використання слів-числівників, а лише зоровим, руховим та зоровим аналізом кількості предметів контрастних множин (один – багато) та рівності-нерівності множин. У цьому віці діти спроможні до висновку, який є підставою до засвоєння принципу утворення натурального числа додавання (віднімання) одиниці. А саме: якщо докладати предмети по одному, то їх стає більше. У доцифровий період лічильної діяльності діти вправляються у різних видах роботи з множинами (утворюють нові множини за певними ознаками, виокремлюють або виділяють окремі елементи, оцінюють їх, вказують на їх властивості чи відмінності).

Лічбу будемо розглядати двояко: як процес та результат. Лічба як процес передбачає встановлення взаємнооднозначної відповідності між елементами певного класу множин, тоді як результат лічби позначається в усному мовленні числівником, а у письмовому поданні – цифрою.

Формування слухового образу числа відносимо до молодшого дошкільного віку. Ним діти оволодівають у ситуаціях, коли дорослі промовляють, показуючи на множину предметів або використовуючи у розмові, числівники. Звертаючись до дитини, дорослі говорять: «Принеси одну книгу», «Дістань дві іграшки», «Купила два кілограми борошна», «Полетіло п’ять пташок», «Одягни два чобітки» тощо.

Навчання лічильної діяльності в організованому середовищі ДНЗ передбачає використання аксіоми лічби, у якій поєднуються поняття потужності множин, дії дитини та назви числівників в єдине і цілісне сприймання і засвоєння натурального числа.

Для ознайомлення з числом і цифрою один можна запропонувати завдання з наочністю.

Таких завдань може бути два. Перше із них передбачає порівняння контрастних множин, у яких один та багато елементів.

Інше завдання полягає у демонстрації на набірному полотні (фланелографі) кількох предметів по одному, яка супроводжується вербальним промовлянням: «Одне поросятко, одна качечка, одне дерево, одна мавпочка, одна полуничка. Цих предметів по одному або один». Згодом виставляється цифра 1.

Ознайомлення з числом 2 може бути виконано за допомогою методичних підходів: 1) як результату лічби предметів; 2) як результату приєднання до одного предмета ще одного; 3) на основі порівняння чисельності множин; 4) як спільне, що є у кількох множинах, а саме кількість.

Подамо зразок мовлення у вивченні числа 4 як потужності рівночислених множин:

Поставимо на набірному полотні рибки. Полічимо їх. Всього рибок чотири. Нижче на набірному полотні виставляємо курчат. Під кожною рибкою ставимо одне курча. Курчат стільки ж, скільки рибок. Курчат на набірному полотні теж чотири. Їх однаково. Під курчатами поставимо зображення ягоди малини. Ягід стільки ж, скільки курчат і стільки рибок або чотири.

Кількість рибок, курчат та малини однаково, по чотири. Поставимо цифру 4.

Закріплення кількісної лічби з використанням слів-числівників можна проілюструвати на завданні, коли усне лічба поєднується із чисельністю відповідних множин.

Один Два Три Чотири П’ять

Розглянемо питання порівняння чисел у межах п’яти. Можна вказати два види завдань: 1) порівняння числа, що вивчається, з одиницею; 2) порівняння чисел у межах числа, що вивчається.

Розглянемо приклад порівняння чисел у межах чотирьох.

Діти, порівняємо числа 4 та 3. Яке із чисел більше, а яке менше? Поставимо на набірному полотні поставимо равликів, а під ними кошенят.

Скільки всього равликів? (4) Скільки всього кошенят? (3) Чи однаково їх? (Ні, неоднаково) Чому неоднаково? (Під одним равликом немає кошеняти) Чого більше? (Равликів більше). На скільки равликів більше? (Равликів більше на один) Чого менше? (Кошенят менше, ніж равликів) Висновок: Равликів більше, ніж кошенят. Отже; 4 більше 3.

Наступним завданням є побудова натурального ряду чисел від 1 до 5.

На основі знань про усну нумерацію, слуховий образ числа будується відрізок натурального ряду чисел. Завдання на закріплення знань про ряд чисел:

1) Назви числа по порядку від меншого до більшого.

2) Назви числа від більшого(5) до меншого.

3) Назви числа, більші за 3.

4) Постав цифри у порядку зростання.

5) Віднови порядок слідування чисел.

У старшому дошкільному віці формується просторовий образ числа. Лічильна діяльність дітей зосереджується на кількісних відношеннях, а не позиційних чи метричних характеристиках множин. Діти розрізняють процес та результат кількісної лічби та роблять висновок про те, що кількість не залежить від величини предметів, їх розташування на площині чи у просторі.

Серед показників сформованості навичок лічильної діяльності у старших дошкільників визначено називання чисел у межах першого десятка; співвіднесення числа з цифрою, цифри з кількістю елементів певної множини і навпаки; лічби у прямому і зворотному напрямах; виконання кількісної та порядкової лічбу; знання послідовності натурального ряду чисел, відновлення порядку чисел (від меншого до більшого і навпаки) та складу чисел у межах 10 (напам’ять у межах 5).

Порівняння чисел першого десятка за методичним підходом аналогічний порівнянню чисел у межах п’яти.

Традиційно склад чисел вивчався на роздавальній наочності, яку можна використовувати у практичних діях. Наприклад, при вивченні складу числа 7 елементи однієї і тієї ж множини можна по-різному перегруповувати: розкласти предмети на столі по одному (Висновок: Сім – це один та один та . . . ) або покласти справа два предмети, а інші – зліва (Сім – це два та п’ять); вліво відкласти три предмети, а чотири вправо (Сім – три та чотири) і т. д.

Інший варіант закріплення складу чисел, починаючи із числа і цифри 5, полягає в тому, що теоретичною основою виступає математична операція розбиття множини на класи за певною ознакою. Відповідно до означення класи розбиття повинні бути не порожніми множинами, не мати спільних елементів, а їх об’єднання давати дану множину. За таких умов вивчення складу чисел у межах 10 дітям шостого року життя пропонується комплект індивідуального роздавального матеріалу для кожного із чисел в межах 10. Мета завдань – подати різні варіанти дихотомічного розбиття множини на класи та закріпити склад чисел в межах 10. Спосіб виконання: оперування предметною множиною для кожного із чисел 5 – 10.

Логічним обґрунтуванням вивчення складу чисел в межах 10 на основі дихотомічного розбиття множини на класи виступають закони тотожності та непротиріччя, оскільки основою поділу в усіх випадках є постійна ознака – властивості предметів.

Для вивчення складу чисел у межах першого десятка дітьми старшого дошкільного віку доцільно використовувати предметні малюнки: для числа 5 – грибів, що відрізняються формою та величиною, книг, що відрізняються товщиною і шириною; для числа 6 – м’ячів, що відрізняються величиною та кольором; для числа 7 – олівців, що відрізняються довжиною та кольором; для числа 8 – квітів, що відрізняються кількістю пелюсток та кольором; для числа 9 – кубиків, різних за величиною та кольором; для числа 10 – геометричних фігур, що відрізняються формою та кольором.

Проілюструємо ознайомлення зі складом, наприклад, числа 7 на основі розбиття множини на класи еквівалентності.

Наочність (демонстраційна, роздавальна). Об’єкти дії – циліндри.

Ознака розбиття: колір, величина.

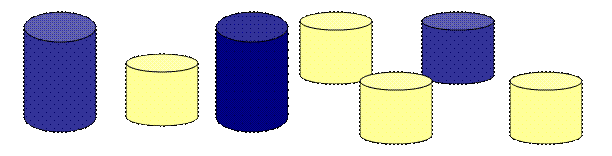
Склад числа 1 та 6. Вибрати маленький синій циліндр (1), та інші (6).

Склад числа 2 та 5. Вибрати великі сині циліндри (2) та інші (5).

Склад числа 3 та 4. Вибрати сині циліндри (3) та інші (4).

Склад числа 4 та 3. Вибрати маленькі жовті циліндри (4) та інші (3).

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.006 сек.