• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

ПРИ СИНУСОЇДНIЙ ДIЇ

ПЕРЕХIДНI ПРОЦЕСИ У КОЛАХ RL, RC, RLC

5.1 Увiмкнення джерела синусоїдної дiї до кола RC

Розв'яжемо задачу аналiзу коливань для кола RC (рис.5.1а) при синусоїднiй дiї 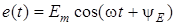. У положеннi 2 перемикача S визначаються початковi умови: ; у положенні 1 коло замикається.

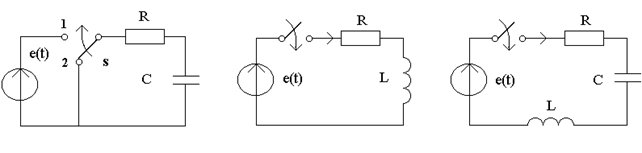
а) б) в)

Рисунок 5.1

Згiдно з другим законом Кiрхгофа

; ; ;

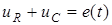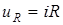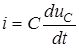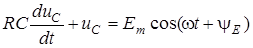. (5.1)

За класичним методом розв’язок (5.1) шукаємо у виглядi

; ; ; .

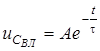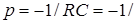
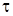Оскiльки дiя є синусоїдною, вимушена складова визначається методом комплексних амплiтуд.

; .

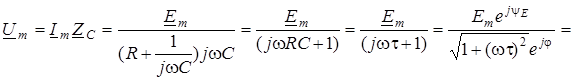
Перейдемо вiд комплексної амплiтуди до миттєвого значення

,

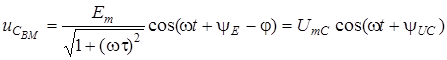де ; .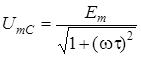

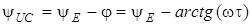Отже, .

Коефiцiєнт A визначається з початкових умов:

; ; .

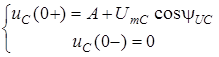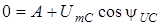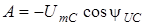Визначивши A, маємо

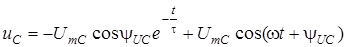. (5.2)

Згiдно з (5.2), напруга на ємностi дорівнює сумі двох складових, при цьому 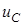залежить вiд величини 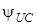. Розглянемо два характерних випадки.

1. Припустимо, що в момент увiмкнення джерела миттєве значення вимушеної складової дорiвнює нулю. Це можливо, якщо . Тодi 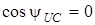, , 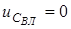нiяких перехiдних процесiв не виникає, i у колi вiдразу встановлюється стацiонарний режим.

2. У загальному випадку, коли 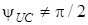; 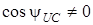, спад напруги на ємностi, як це видно з (5.2), може суттєво вiдрiзнятися вiд напруги вимушених коливань . Найбiльш характерним у цьому вiдношеннi є перехiдний процес, який спостерiгається при 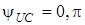(рис.5.2а). У нульовий момент часу сума напруг 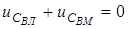. Потiм виникає перехiдний процес, який закiнчується через промiжок часу 4,6t. При вiльна складова практично дорiвнює нулю, i графiк збігається з кривою . Як бачимо, пiсля замикання ключа через промiжок часу, який приблизно дорiвнює половинi перiоду вiльних коливань, напруга 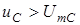. Максимальна напруга на ємностi може бути бiльшою нiж амплiтуда синусоїдної дiї майже у два рази (особливо, якщо стала часу велика).

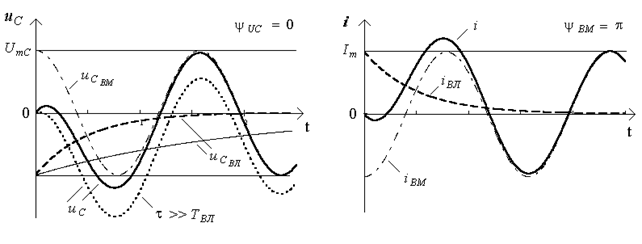а) б)

Рисунок 5.2

5.2 Увiмкнення джерела синусоїдної дiї до кола RL

Розв'яжемо задачу аналiзу коливань для кола RL (рис.5.1б) при синусоїднiй дiї 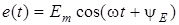, виключаючи етап складання диференцiйного рiвняння, за нульових початкових умов. Тоді запишемо

.

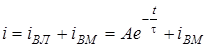Вимушену складову знайдемо за допомогою методу комплексних амплiтуд

,

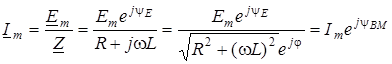де ; ; .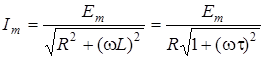

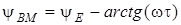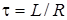Тодi .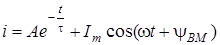

Коефiцiєнт A визначимо з початкових умов:

; ; .

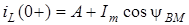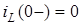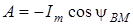Визначивши A, маємо

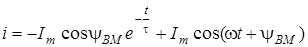. (5.3)

Аналогiчно з попереднiм роздiлом маємо два характерних випадки.

1. Вiдсутнiсть перехiдного процесу, коли 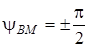. При цьому у початковий момент часу вимушена складова струму дорiвнює нулю, вiльний струм вiдсутнiй, i у колi вiдразу встановлюється стацiонарний стан.

2. У загальному випадку вимушена складова струму у початковий момент вiдрiзняється вiд нуля, i у колi спостерiгається перехiдний процес (рис.5.2б). З рисунка видно, що у початковий момент часу перехiдний струм помiтно вiдрiзняється за формою вiд вимушеного струму, причому у деяких точках величина його перебiльшує .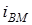

Максимально можливi значення струму у колi, як це виходить з (5.3), спостерiгаються за умови, коли вимушена складова у момент часу 0+ має максимальне значення, тобто при 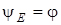або . Якщо стала часу велика, то на iнтервалi, де , максимуми струму наближаються до .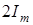

5.3 Увiмкнення джерела синусоїдної дiї до кола RLC

Розглянемо перехiднi процеси у колi RLC при увiмкненнi джерела гармонiчної дiї за нульових початкових умов: ; .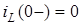

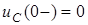Нехай функцiя зовнiшньої дiї при 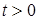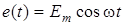, . Пiсля комутацiї створюється коло, яке описується за другим законом Кiрхгофа (рис.5.1в):

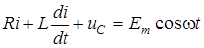. (5.4)

Оскiльки 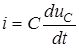, отримуємо диференцiйне рiвняння

.

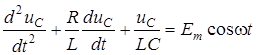Розв'язок шукаємо у виглядi . Результат залежить вiд характеру коренiв 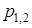. Найбiльш цiкавим є випадок комплексно-спряжених коренiв, оскiльки це вiдповiдає великому значенню добротностi (при цьому має мiсце явище резонансу). Тодi

; .

Визначимо вимушену складову методом комплексних амплiтуд:

,

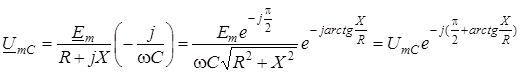де ; .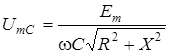

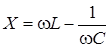Позначимо i перейдемо до миттєвого значення.

.

Отже, напруга на ємностi визначається виразом:

. (5.5)

Вище (лекція 4) було показано, що при , . Крiм того, за таких умов можна показати, що ; .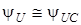

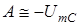При цих припущеннях вираз (5.5) матиме вигляд

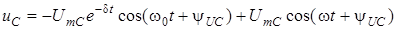. (5.6)

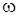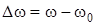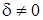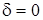Отже, є сумою двох коливань з рiзними частотами. Аналiзуючи (5.6), можна зробити висновок, що характер перехiдних процесiв залежить вiд спiввiдношення мiж частотою коливань зовнiшньої дiї i резонансною частотою . Позначимо абсолютну розстройку i розглянемо три випадки: 1) , ; 2) , ; 3) , .

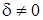1. При , 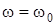маємо

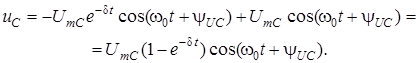
Оскiльки при 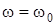у колi виникає явище резонансу, то слушнi спiввiдношення 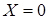; ; 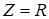; 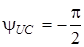. Тодi

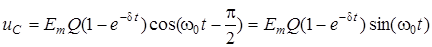. (5.7)

Останнiй вираз можна записати ще як , де 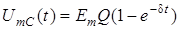- рiвняння обвідної. У даному випадку амплiтуда коливань напруги на ємностi у контурi зростає у часі за експоненцiйним законом, наближаючись до значення .

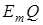Щоб знайти швидкiсть зростання амплiтуди коливань, розрахуємо похiдну 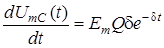у початковий момент часу:

.

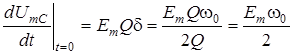Отже, швидкiсть зростання обвідної не залежить вiд значення добротностi. Тому у контурi з бiльшою добротнiстю (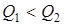) для встановлення стацiонарного режиму потрiбен бiльший час (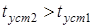, рис.5.3а). Осцилограма спаду напруги на ємностi при вмиканнi i вимиканнi синусоїдної дiї зображена на рис.5.3б.

а) б)

Рисунок 5.3

2. Перейдемо до аналiзу перехiдних явищ у контурi, коли частота зовнiшнiх коливань 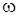не збігається з резонансною частотою. Якщо контур не має втрат (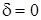), напруга на ємностi являє собою, як це виходить з (5.6), сукупнiсть двох гармонiчних коливань, якi мають близькi частоти i приблизно однаковi амплiтуди. У цьому випадку (5.6) перетворюється у вираз

(5.8)

В результатi пiдсумовування коливань вiльної i вимушеної складових виникають так званi биття (рис.5.4). З рiвняння (5.8) виходить, що амплiтуда 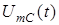повiльно змiнюється у часі за законом

,

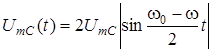а частота коливань дорiвнює . Биття будуть протiкати з подвоєною амплiтудою, оскiльки у випадку однакових фаз векторiв 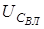i 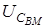, цi вектори спрямованi однаково, i тому їх амплiтуди пiдсумовуються. Перiод биттiв розглядають як величину, що у два рази менша за перiод синусоїди, тобто .

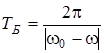Рисунок 5.4

3. У реальному контурi (коли 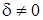) величина вiльної складової зменшується за експоненцiйним законом. Внаслiдок цього при i 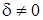обвідна перехiдного процесу матиме складніший вигляд (рис.5.5). Аби пояснити формування виду обвідної, слiд розглянути векторну дiаграму (рис.5.6).

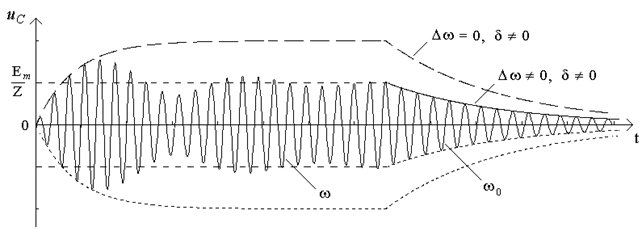
Рисунок 5.5

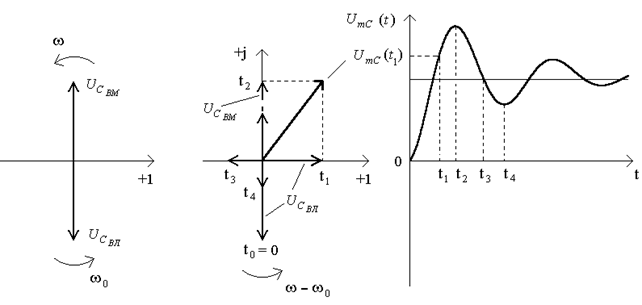
Рисунок 5.6

Переглядів: 613