• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Эти частицы находятся в непрерывном хаотическом (тепловом) движении

Основные положения МКТ и их опытное обоснование

МОЛЕКУЛЯРНАЯ ФИЗИКА

Лекция 8

Опукле програмування

Опукле програмування розглядає методи розв’язування задач нелінійного програмування, математичні моделі яких містять опуклі або угнуті функції.

Загальний вигляд задачі опуклого програмування такий:

, (7.27)

, ; (7.28)

, (7.29)

де , – угнуті функції.

Аналогічний вигляд має задача для опуклих функцій.

Позначимо: , тоді , і маємо:

, (7.30)

; (7.31)

, (7.32)

де , – опуклі функції.

Оскільки ці задачі еквівалентні, то нижче розглянемо задачу (7.27)-(7.29).

Множина допустимих планів задачі, що визначається системою (7.28), є опуклою.

Як наслідок теорем 7.2 та 7.3 справджується таке твердження: точка локального максимуму (мінімуму) задачі опуклого програмування (7.27)-(7.29) є одночасно її глобальним максимумом (мінімумом).

Отже, якщо визначено точку локального екстремуму задачі опуклого програмування, то це означає, що знайдено точку глобального максимуму (мінімуму).

У разі обмежень-нерівностей задачу опуклого програмування розв’язують, застосовуючи метод множників Лагранжа.

Функція Лагранжа для задачі (7.27)-(7.29) має вид:

(7.33)

де – множники Лагранжа.

Використовуючи теорему Куна-Таккера, маємо необхідні та достатні умови існування оптимального плану задачі опуклого програмування.

Теорема 7.4. Якщо задано задачу нелінійного програмування виду (7.27)-(7.29), де функції диференційовні і вгнуті по Х, то для того, щоб вектор був розв’язком цієї задачі, необхідно і достатньо, щоб існував такий вектор , що пара ( , ) була б сідловою точкою функції Лагранжа, тобто щоб виконувалися умови:

(І) , ; (7.34)

(ІІ) , ; (7.35)

(ІІІ) , ; (7.36)

(IV) , . (7.37)

Для задачі мінімізації (7.30)-(7.32), де всі функції диференційовні і опуклі по Х, маємо умови, аналогічні вищенаведеним, але зі знаком «≥» в нерівностях (7.35) та (7.37).

Молекулярно-кинетическая теория строения вещества (МКТ)__________________ ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

1. Все тела состоят из частиц – атомов и молекул.

Это можно доказать, ________________________________________________________ ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

______________________________________________________________________________________________________________________________________________________

Опытные доказательства – ________________________________________________

Диффузия –_______________________________________________________________ ___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Броуновское движение – ____________________________________________________ _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Экспериментальное исследование броуновского движения – Жан Перрен.

Траектория броуновской частицы.

3. Частицы взаимодействуют друг с другом силами притяжения и отталкивания.

Опытные доказательства – ____________________________________________________ _________________________________________________________________________________________________________________________________________________________________________________________________________________________________

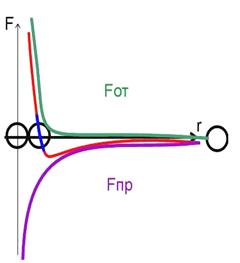Fот – ______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Fпр - ______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Третья кривая - ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Линейный участок ____________________________________________________________________________________________________________________________________________________________________________

Читайте також:

1. Потери напора по длине при равномерном ламинарном движении жидкости

Переглядів: 730