• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Узагальнений закон Гука.

Для сумісного розгляду теорії напружень та теорії деформацій потрібно встановити залежність між напруженнями та деформаціями. Ця залежність має фізичний характер. Для лінійно - пружних ізотропних тіл фізичні рівняння представляють собою співвідношення узагальненого закону Гука, відомого з курсу “Опір матеріалів”:

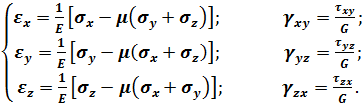(3.21)

де E, G, μ – модуль поздовжньої пружності, модуль пружності при зсуві та коефіцієнт Пуассона, відповідно.

Останні рівняння виражають лінійну залежність між складовими деформації та напруження ми в ізотропному пружному тілі.

При розв’язку задач інколи потрібно мати формули в яких складові напружень виражені через складові деформацій. Для їх отримання складемо ліві та праві частини перших трьох формул (3.21):

Згідно виразів (3.13) та (2.8):

остання формула набуде вигляду:

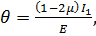(3.22)

тобто відносна об’ємна деформація θ пропорційна першому інваріанту напруженого стану І₁. Введемо в розрахунок модуль об’ємного розширення:

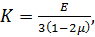
отримаємо:

(3.23)

Якщо перший інваріант напруженого стану І₁ замінити потроєним середнім напруженням в точці , то замість рівняння (3.23) отримаємо:

(3.24)

Останнє рівняння говорить про те, що середнє напруження в точці пропорційне об’ємній деформації.

Для того щоб виразити складові напруження через складові деформації скористаємося першою формулою закону Гука (3.21), додаючи та віднімаючи в квадратних дужках величину μσ_х:

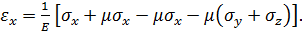
З отриманого виразу виділимо перший інваріант напруженого стану I₁:

(3.25)

Виразимо з формули (3.22) перший інваріант напруженого стану:

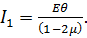(3.26)

Підставимо формулу (3.26) в формулу (3.25):

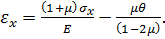
З останньої формули виразимо σ_х:

(3.27)

Введемо позначення:

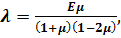
та відома з курсу опір матеріалів залежність:

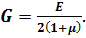
Тоді замість формули (3.27) отримаємо:

Аналогічно останньому виразу, можна отримати формули для обчислення σ_y, σ_z. Після цього є змога записати так званий обернений закон Гука:

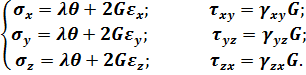(3.28)

В частину формул (3.28) входить коефіцієнт λ, що називають коефіцієнтом Ламе, який характеризує пружні властивості матеріалу.

Складемо між собою праві та ліві частини перших трьох формул (3.28):

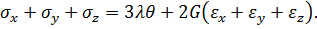
Враховуючи, що ліва частина останнього рівняння представляє собою перший інваріант напруженого стану, а права частина в дужках відносну об’ємну деформацію, формула набуде вигляду:

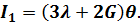(3.29)

Останнє співвідношення встановлює зв'язок між першими інваріантами напруженого стану та деформованого стану через коефіцієнти Ламе. Замінивши в останньому виразі перший інваріант напруженого стану І₁ на потроєне середнє напруження в точці σ₀, а об’ємну деформацію θ – потроєною усередненою деформацією в точці отримаємо:

(3.30)

Рівняння (3.30) представляє собою ще одну форму закону Гука – середнє напруження в точці прямо пропорційне середньому подовженню в цій точці.

Читайте також:

1. II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
2. IV. Закони ідеальних газів.
3. IV. Закономірності структурно-функціональної організації спинного мозку
4. Авілум – “син чоловіка” – повноправна людина, охороні його життя, здоров’я, захисту його майнових інтересів присвячена значна частина законника.
5. Аграрне право та законодавство США, Німеччини, Франції, Великої Британії, Ізраїлю, Польщі, Росії
6. Аграрні закони України
7. Адаптація законодавства України до законодавства ЄС - один із важливих інструментів створення в Україні нової правової системи та громадянського суспільства
8. Адаптація законодавства України до законодавства ЄС - один із важливих інструментів створення в Україні нової правової системи та громадянського суспільства
9. Адміністративна відповідальність за порушення аграрного законодавства
10. Адміністративна відповідальність за порушення земельного законодавства
11. Адміністративна відповідальність за порушення податкового законодавства.
12. Адміністративна відповідальність осіб, винних в порушенні податкового законодавства

Переглядів: 2984