• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Узагальнений закон Гука.

3.1. Складові переміщення, деформацій. Геометричні співвідношення Коші.

Дослідимо деформацію пружного тіла. Для її визначення порівняємо положення точок тіла до та після прикладання навантаження. На рис. 10 показано тіло та точка А з координатами x, y, z. Під дією навантаження точка А переміститься в нове положення А' з координатами x', y', z'. Вектор АА' носить назву – вектор переміщення точки А.

Розрізняють два види переміщень: переміщення всього тіла як єдиного цілого без його деформації та переміщення, пов’язане з деформуванням тіла. Переміщення першого виду вивчають в теоретичній механіці як переміщення абсолютно твердого тіла. В теорії пружності розглядають тільки переміщення, пов’язані з деформуванням тіла.

Будемо вважати, що розглядуване тіло закріплено таким чином, що воно не може переміщуватися, як абсолютно тверде тіло. Позначимо проекції вектора переміщення точки А на координатні осі через u, w, z. Вони дорівнюють різниці відповідних координат точок А та А':

На рис. 3.2 зображено два ребра цього паралелепіпеду: ребро АВ, паралельне осі х, та ребро АС, паралельне осі y. Довжина ребра АВ дорівнює dx, ребра АС – dz. Після деформації точки А, В, С займуть нові положення: А', В', С'. При цьому точка А отримає переміщення, складові якого в площині креслення дорівнюють u та v. Точка В, яка знаходиться на нескінченно малій відстані dx від точки А, отримає переміщення, складові якого будуть відрізнятися від складових переміщення точки А на нескінченно малу величину за рахунок зміни координати х:

Складові переміщення точки С будуть відрізнятися від складових переміщення точки А на нескінченно малу величину за рахунок зміни координати y:

Довжина проекції ребра АВ на вісь х після деформації:

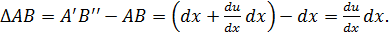(3.2)

Відносна деформація вздовж осі х:

. (3.3)

Вираз (3.3) називають лінійною деформацією за напрямком осі х.

Аналогічно можна отримати лінійну деформацію за напрямком координатних осей y та z:

(3.4)

Отже, лінійна деформація в будь-якому напрямку дорівнює частній похідній складової переміщення в цьому напрямку за змінною в цьому ж напрямку.

Розглянемо зміни кутів між ребрами паралелепіпеду (рис. 3.2). Тангенс кута повороту ребра АВ в площині xOy:

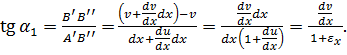(3.5)

Обмежуючись розглядом тільки малих деформацій, можна прийняти tgα₁ ≈ α₁ та нехтуючи лінійною деформацією ε_х, як нескінченно малою у порівнянні з одиницею, отримаємо:

(3.6)

Аналогічно можна визначити кут повороту ребра АС в цій же площині:

(3.7)

Кут зсуву в площині xOy, тобто зміну попередньо прямого кута ВАС, називають кутовою деформацієюта визначають як суму кутів повороту ребер АВ та АС:

(3.8)

Аналогічно знаходять кутові деформації в двох інших координатних площинах:

(3.9)

Кутова деформація в будь-якій площині дорівнює сумі частних похідних складових переміщення в цій площині по переміщенню в перпендикулярних напрямках.

Формули (3.3), (3.4), (3.8), (3.9) дають шість основних залежностей складових лінійних та кутових деформацій від складових переміщення:

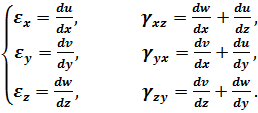(3.10)

Останні залежності називають геометричними співвідношеннями Коші.

Переходячи до межі, коли ребра паралелепіпеду прямують до нуля, формули (3.10) визначають лінійні та кутові деформації біля точки А.

Правило знаків для складових деформації:

- додатнім лінійним деформаціям відповідає подовження за відповідними напрямками, а від’ємним – скорочення;

- додатнім кутовим деформаціям відповідає зменшення кутів між додатнім напрямком координатних осей, а від’ємним – збільшення цих же кутів.

У випадку, коли потрібно знайти об’ємну деформацію, розглядають нескінченно малий паралелепіпед об’ємом dV = dxdydz. Вважають, що зміна цього об’єму пов’язана тільки зі зміно довжини ребер, а кутовими деформаціями нехтують, як більшого порядку малості.

Довжина ребра АВ, яка попередньо дорівнювала dx, після деформування відповідно до (3.1) дорівнює:

Скориставшись першим рівнянням (3.10), отримаємо:

(3.11)

Аналогічно отримують довжини інших ребер після деформації:

(3.12)

Об’єм паралелепіпеду після деформації дорівнює:

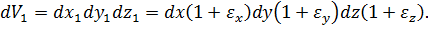
Розкривши дужки, отримаємо:

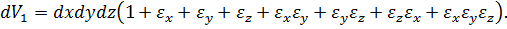
Нехтуючи в дужках величинами другого та третього порядків малості та враховуючи, що dxdydz = dV, знайдемо:

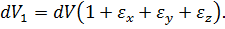
Позначимо відносну зміну об’єму 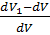через θ та отримаємо:

(3.13)

Таким чином, об’ємна деформація дорівнює сумі лінійних деформацій за трьома перпендикулярними напрямками.

Використовуючи рівняння (3.10) об’ємну деформацію можна виразити через складові переміщення:

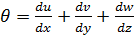. (3.14)

3.2. Рівняння неперервності деформацій.

Геометричні співвідношення Коші (3.10) пов’язують між собою шість складових деформації ε_x, ε_y, ε_z, γ_xz, γ_yx, γ_zy та три складових переміщення u, v, w. Якщо задані три складові переміщення, то їм відповідає єдина система шести складових деформацій.

Якщо задані шість складових деформацій, то для визначення трьох складових переміщення потрібно про інтегрувати шість диференціальних рівнянь (3.10) в частних похідних. При довільному виборі складових деформацій шість рівнянь з трьома незалежними не завжди можуть бути вирішені однозначно. Тому між шістьома складовими деформації повинні існувати певні залежності. Щоб отримати ці залежності, виключимо складові переміщення з рівнянь (3.10). Продиференцюємо перш рівняння (3.10) двічі по y, а друге по х:

Складемо ліві та праві частини отриманих рівнянь:

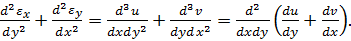(3.15)

Вираз в дужках, відповідно до (3.10), визначає кутову деформацію γ_yx. З урахуванням цього вираз (3.15) набуде вигляду:

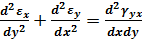. (3.16)

За аналогією встановимо залежності між двома деформаціями в двох інших координатних площинах:

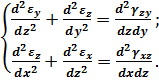(3.17)

Рівняння (3.16), (3.17) показують, що якщо задані дві лінійні деформації у взаємно перпендикулярних напрямках, то кутову деформацію в площині цих лінійних деформацій неможливо задати довільно.

Трьох рівнянь (3.16), (3.17) недостатньо для забезпечення однозначності переміщень, оскільки вони отримані диференціюванням. При диференціюванні порядок диференціального рівняння підвищується і можлива поява нових рішень, які не задовольняють початковому рівнянню. Щоб запобігти отриманню неприйнятних рішень, потрібно мати додаткові умови.

Продиференцюємо три останні рівняння (3.10) наступним чином:

Складемо перші дві строки та віднімемо третю:

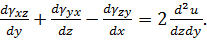
Продиференцюємо отримане рівняння ще раз по x та, враховуючи, що:

отримаємо:

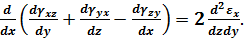(3.18)

Аналогічно можна отримати ще два рівняння:

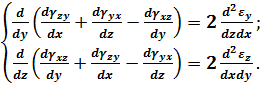(3.19)

Рівняння (3.18), (3.19) свідчать про те, що якщо задані три кутові деформації в трьох взаємно перпендикулярних площинах, то лінійні деформації не можуть бути задані довільно.

Отже, отримана наступна система рівнянь, що носять назву рівнянь неперервності деформаційСен-Венана:

(3.20)

Необхідність існування отриманих залежностей можна обґрунтувати і геометричним шляхом. Уявимо тіло розрізане на нескінченно малі паралелепіпеди. Якщо кожен з цих паралелепіпедів отримає довільні деформації, то з окремих деформованих паралелепіпедів неможливо буде знову скласти неперервне тверде тіло (в частині точок після деформування виникнуть нескінченно малі розриви). Рівняння (3.20) встановлює такі залежності між складовими деформації, що тіло і після деформування залишаться суцільним.

Читайте також:

1. II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
2. IV. Закони ідеальних газів.
3. IV. Закономірності структурно-функціональної організації спинного мозку
4. Авілум – “син чоловіка” – повноправна людина, охороні його життя, здоров’я, захисту його майнових інтересів присвячена значна частина законника.
5. Аграрне право та законодавство США, Німеччини, Франції, Великої Британії, Ізраїлю, Польщі, Росії
6. Аграрні закони України
7. Адаптація законодавства України до законодавства ЄС - один із важливих інструментів створення в Україні нової правової системи та громадянського суспільства
8. Адаптація законодавства України до законодавства ЄС - один із важливих інструментів створення в Україні нової правової системи та громадянського суспільства
9. Адміністративна відповідальність за порушення аграрного законодавства
10. Адміністративна відповідальність за порушення земельного законодавства
11. Адміністративна відповідальність за порушення податкового законодавства.
12. Адміністративна відповідальність осіб, винних в порушенні податкового законодавства

Переглядів: 934