Boolean Algebra

One should know when and where the idea of laying down postulates for the manipulation of abstract symbols (not necessarily numbers) first occurred and who was the creator of such an abstract algebra (= who the creator of such an abstract algebra was). It occurred first in England and at about the time of George Boole (1815-1864), the English mathematician and logician. One can doubt whether Boolean algebra, i.e., the algebra of sets, studied largely by means of truth tables, has anything to do with computers; whether basic laws of ordinary algebra (commutative, associative and distributive) hold in Boolean algebra, etc. The most recent development in connection with Boolean algebra is its application to the design of electronic computers through the interpretation of Boolean combinations of sets as switching circuits. The answer to the question of what part of Boolean algebra is used so widely in cybernetics may surprise the uninitiated – the limited special type of Boolean algebra having only two elements in it which at first sight may seem impractical at all is the very one used too widely nowadays. The basic electronic device in the early computers was the vacuum tube which was turned off or on by the electric current entering the tube. Boolean logical product of two sets corresponds to a circuit with two switches in series. It is easy to realize when electricity flows in such a circuit – only if both the first and the second switches are closed. The logical sum of two sets corresponds to a circuit with two switches in parallel. The question whether electricity can flow in such a circuit has the following answer: electricity flows in such a circuit if either one or the other or both switches are closed. Telephone circuits and electronic computers are basically designed upon a system of Boolean symbolic logic.

The fundamental components of any digital computer are, thus, switches capable of two different states of transmission. The speed of the computer in its calculations is limited by the time, required for a switch to change states, among other factors. In general, it is desirable that a switch should consume as little power as possible. No switching computer circuit acts instantaneously. One may wonder what it means in practice. It means that there is a brief delay between the instant incoming signals appear on the input leads and the instant an outgoing signal appears on the output lead. In the days of vacuum-tube circuitry the delay was about 10 microseconds (millionths of a second). Some of today's circuits have a delay of the nanosecond (a billionth of a second). Large or small switching delay is a factor that affects the speed of a computation. Called delay time, it is represented by 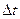. One may inquire how fast modern computers can add. Today they can add at a rate of 10 million calculations per second; it is not a limit of course. In a current electronic computer virtually all the switches are transistors, and even the fastest transistors now in use cannot be made to change states in less than about a nanosecond, or a billionth of a second. An optical device analogous to the transistor that has recently been developed can switch from one transmission state to the other in about a picosecond or a thousandth of a billionth of a second.

The three basic functions of a computer – arithmetic operations, logical operations and the storage of information or memory – are all done by devices that have two stable states. In arithmetic operations the two states represent the numerals 0 and 1 of the binary number system. In the evaluations of logical propositions the two states stand for true of false. The memory of the computer stores the results of arithmetic and logical operations in devices that occupy one of the two states. With the binary algebraic system a computer can evaluate the truth of propositions by making use of just three logical functions, which are usually referred to as the ANDfunction, the ORfunction and the NOTfunction. In the ANDfunction a statement is taken as true if all its components are true. In the ORfunction a statement is taken as true if any of its components is true. In the NOTfunction the truth value of a statement is reversed. More elaborate logical operations can be built out of the three basic functions, and so can arithmetic operations such as addition. Thus, a computer requires a device that can represent the values 0 and 1, or true or false in physical form that can be assembled into large-scale devices that perform the three logical functions. By combining transistors and other circuit elements, structures that carry out the AND, OR, or NOT functions can be assembled.

Reasonable operations are logical and math operations. Math operations include addition, subtraction, multiplication, division, taking square root, etc., and also more advanced math operations such as raising to a power, finding derivatives and integrating. Logical operations include comparing, selecting, sorting, matching, determining, the next instruction which is to be performed, etc.

4.	1. Artificial Intelligence. It is Possible?
2. Turing’s Test.
3. To be One with the Computer.
4. Modal Verbs[5].

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Writing	\|

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.002 сек.