Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Text 2. The Insolubility of Hilbert's Problem

Internet Assignment:

Use the Internet and provide answers to these questions:

1. What directions and tendencies in the 19^th century maths gave implications and led D.Hilbert to formulating those particular problems?

2. How do the 20^th century mathematicians estimate the solution of any problem in D.Hilbert’s list?

3. Who solved D.Hilbert’s 10^th problem? When?

4. What is the contribution of the Ukrainian mathematicians to the solution of the problems under study?

5. Are the unsolved problems the very essence of maths?

We now come to the purpose for which Turing originally put forward his ideas, the resolution of Hilbert's broad-ranging Entscheidungsproblem: is there some mechanical procedure for answering all mathematical problems, belonging to some broad, but well-defined class? Turing found that he could phrase his version of the question in terms of the problem of deciding whether or not the 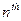Turing machine would actually ever stop when acting on the number 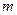. This problem was referred to as the halting problem. It is an easy matter to construct an instruction list for which the machine will not stop for any number m (for example, 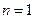or 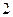, as given above, or any other case where there are no stop instructions whatever). Also there are many instruction lists for which the machine would always stop, whatever number it is given (e.g. 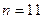); and some machines would stop for some numbers but not for others. One could fairly say that a putative algorithm is not much use when it runs forever without stopping. That is no algorithm at all. So an important question is to be able to decide whether or not T_n applied to m actually ever gives any answer! If it does not (i.e. if the calculation does not stop), then I shall write □.

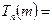(Included in this notation would be those situations where the Turing machine runs into a problem at some stage because it finds no appropriate instruction to tell it what to do – as with the dud machines such as 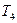and 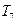considered above. Also, unfortunately, our seemingly successful machine 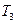, must now also be considered a dud: 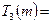, because the result of the action of 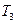is always just blank tape, whereas we need at least one 1 in the output in order that the result of the calculation be assigned a number! The machine 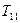is, however, legitimate since it produces a single 1. This output is the tape numbered 0, so we have 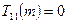for all m.)

It would be an important issue in mathematics to be able to decide when Turing machines stop. For example, consider the equation:

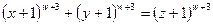(If technical mathematical equations are things that worry you, don't be put off! This equation is being used only as an example, and there is no need to understand it in detail.) This particular equation relates to a famous unsolved problem in mathematics – perhaps the most famous of all. The problem is this: is there any set of natural numbers w, x, y, z for which this equation is satisfied? The famous statement known as 'Fermat's last theorem', made in the margin of Diophantus's Arithmetica, by the great seventeenth century French mathematician Pierre de Fermat (1601-1665), is the assertion that the equation is never satisfied.[12] Though a lawyer by profession (and a contemporary of Descartes), Fermat was the finest mathematician of his time. He claimed to have a truly wonderful proof of his assertion, which the margin was too small to contain; but to this day no-one has been able to reconstruct such a proof nor, on the other hand, to find any counter-example to Fermat's assertion!

It is clear that given the quadruple of numbers (w, x, y, z), it is a mere matter of computation to decide whether or not the equation holds. Thus we could imagine a computer algorithm which runs through all the quadruples of numbers one after the other, and stops only when the equation is satisfied. (We have seen that there are ways of coding finite sets of numbers, in a computable way, on a single tape, i.e. simply as single numbers, so we can 'run through' all the quadruples by just following the natural ordering of these single numbers.) If we could establish that this algorithm does not stop, then we would have a proof of the Fermat assertion.

In a similar way it is possible to phrase many other unsolved mathematical problems in terms of the Turing machine halting problem. Such an example is the 'Goldbach conjecture', which asserts that every even number greater than 2 is the sum of two prime numbers.[13] It is an algorithmic process to decide whether or not a given natural number is prime since one needs only to test its divisibility by numbers less than itself, a matter of only finite calculation. We could devise a Turing machine which runs through the even numbers 6, 8,10, 12, 14, ... trying all the different ways of splitting them into pairs of odd numbers

, , ,

, , …

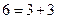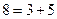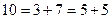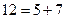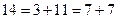and testing to make sure that, for each such even number, it splits to some pair for which both members are prime. (Clearly we need not test pairs of even summands, except 2 + 2, since all primes except 2 are odd.) Our machine is to stop only when it reaches an even number for which none of the pairs into which that number splits consists of two primes. In that case we should have a counter-example to the Goldbach conjecture, namely an even number (greater than 2) which is not the sum of two primes. Thus if we could decide whether or not this Turing machine ever stops, we should have a way of deciding the truth of the Goldbach conjecture also.

A natural question arises: how are we to decide whether or not any particular Turing machine (when fed with some specific input) will ever stop? For many Turing machines this might not be hard to answer; but occasionally, as we have seen above, the answer could involve the solution of an outstanding mathematical problem. So, is there some algorithmic procedure for answering the general question – the halting problem – completely automatically? Turing showed that indeed there is not.

His argument was essentially the following. We first suppose that, on the contrary, there is such an algorithm.[14] Then there must be some Turing machine H which 'decides' whether or not the 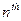Turing machine, when acting on the number m, eventually stops. Let us say that it outputs the tape numbered 0 if it does not stop and 1 if it does:

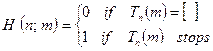Here, one might take the coding of the pair 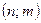to follow the same rule as we adopted for the universal machine 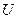. However this could run into the technical problem that for some number 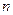(e.g. 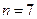), T_n is not correctly specified; and the marker 111110 would be inadequate to separate n from m on the tape. To obviate this problem, let us assume that n is coded using the expanded binary notation rather than just the binary notation, with m in ordinary binary, as before. Then the marker 110 will actually be sufficient to separate n from m. The use of the semicolon in , as distinct from the comma in 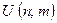, is to indicate this change.

Now let us imagine an infinite array, which lists all the outputs of all possible Turing machines acting on all the possible different inputs. The 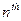row of the array displays the output of the 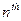Turing machine, as applied to the various inputs 0,1, 2, 3,4, … :

m →										…
n ↓
	□	□	□	□	□	□	□	□	□	…
										…
										…
										…
										…
		□		□		□		□		…
		□		□		□		□		…
										…
	□		□	□		□	□	□		…
.	.				.				.	…
.	.				.				.
.	.				.				.
										…
.	.				.				.
.	.				.				.
.	.				.				.

In the above table I have cheated a little, and not listed the Turing machines as they are actually numbered. To have done so would have yielded a list that looks much too boring to begin with, since all the machines for which n is less than 11 yield nothing but Ds, and for 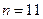itself we get nothing but 0s. In order to make the list look initially more interesting, I have assumed that some much more efficient coding has been achieved. In fact I have simply made up the entries fairly randomly, just to give some kind of impression as to what its general appearance could be like.

I am not asking that we have actually calculated this array, say by some algorithm. (In fact, there is no such algorithm, as we shall see in a moment.) We are just supposed to imagine that the true list has somehow been laid out before us, perhaps by God! It is the occurrence of the Ds which would cause the difficulties if we were to attempt to calculate the array, for we might not know for sure when to place a Din some position since those calculations simply run on forever!

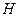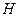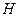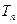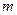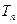However, we could provide a calculational procedure for generating the table if we were allowed to use our putative , for would tell us where the □s actually occur. But instead, let us use to eliminate every □ by replacing each occurrence with 0. This is achieved by preceding the action of on by the calculation ; then we allow to act on m only if (i.e. only if the calculation 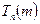actually gives an answer), and simply write 0 if 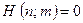(i.e. if 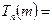□ ). We can write our new procedure (i.e. that obtained by preceding 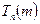by the action of 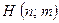)as

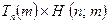(Here I am using a common mathematical convention about the ordering of mathematical operations: the one on the right is to be performed first. Note that, symbolically, we have □ x 0 = 0.) The table for this now reads:

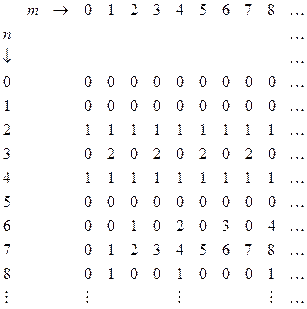
Note that, assuming H exists, the rows of this table consist of computable sequences. (By a computable sequence I mean an infinite sequence whose successive values can be generated by an algorithm; i.e. there is some Turing machine which, when applied to the natural numbers m = 0,1, 2, 3, 4, 5, … in turn, yields the successive members of the sequence.) Now, we take note of two facts about this table. In the first place, every computable sequence of natural numbers must appear somewhere (perhaps many times over) amongst its rows. This property was already true of the original table with its Ds. We have simply added some rows to replace the 'dud' Turing machines (i.e. the ones which produce at least one D). In the second place, the assumption having been made that the Turing machine H actually exists, the table has been computably generated (i.e. generated by some definite algorithm), namely by the procedure 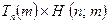. That is to say, there is some Turing machine 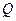which, when acting on the pair of numbers 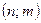produces the appropriate entry in the table. 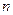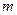For this, we may code and on 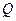's tape in the same way as for 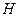, and we have

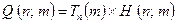We now apply a variant of an ingenious and powerful device, the 'diagonal slash' of Georg Cantor. Consider the elements of the main diagonal, marked now with bold figures:

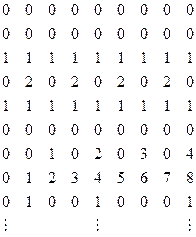
These elements provide some sequence 0, 0, 1, 2, 1,0, 3, 7, 1, … to each of whose terms we now add 1:

1, 1, 2, 3, 2, 1, 4, 8, 2, … .

This is clearly a computable procedure and, given that our table was computably generated, it provides us with some new computable sequence, in fact with the sequence 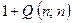, i.e.

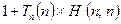
(since the diagonal is given by making m equal to n). But our table contains every computable sequence, so our new sequence must be somewhere in the list. Yet this cannot be so! For our new sequence differs from the first row in the first entry, from the second row in the second entry, from the third row in the third entry, and so on. This is manifestly a contradiction. It is the contradiction which establishes what we have been trying to prove, namely that the Turing machine H does not in fact exist! There is no universal algorithm for deciding whether or not a Turing machine is going to stop.

Another way of phrasing this argument is to note that, on the assumption that H exists, there is some Turing machine number, say k, for the algorithm (diagonal process!) 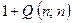, so we have

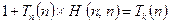But if we substitute 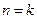in this relation we get

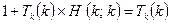This is a contradiction because if 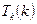stops we get the impossible relation

(since 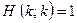), whereas if 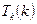does not stop (so 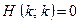) we have the equally inconsistent

□.

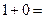The question of whether or not a particular Turing machine stops is a perfectly well-defined piece of mathematics (and we have already seen that, conversely, various significant mathematical questions can be phrased as the stopping of Turing machines). Thus, by showing that no algorithm exists for deciding the question of the stopping of Turing machines, Turing showed (as had Church, using his own rather different type of approach) that there can be no general algorithm for deciding mathematical questions. Hilbert's Entscheidungsproblem has no solution!

This is not to say that in any individual case we may not be able to decide the truth, or otherwise, of some particular mathematical question; or decide whether or not some given Turing machine will stop. By the exercise of ingenuity, or even of just common sense, we may be able to decide such a question in a given case. (For example, if a Turing machine's instruction list contains no stop order, or contains only stop orders, then common sense alone is sufficient to tell us whether or not it will stop!) But there is no one algorithm that works for all mathematical questions, nor for all Turing machines and all numbers on which they might act.

It might seem that we have now established that there are at least some undecidable mathematical questions. However, we have done nothing of the kind! We have not shown that there is some especially awkward Turing machine table for which, in some absolute sense, it is impossible to decide whether or not the machine stops when it is fed with some especially awkward number – indeed, quite the reverse, as we shall see in a moment. We have said nothing whatever about the insolubility of single problems, but only about the algorithmic insolubility of families of problems. In any single case the answer is either 'yes' or 'no', so there certainly is an algorithm for deciding that particular case, namely the algorithm that simply says 'yes', when presented with the problem, or the one that simply says 'no', as the case may be! The difficulty is, of course, that we may not know which of these algorithms to use. That is a question of deciding the mathematical truth of a single statement, not the systematic decision problem for a family of statements. It is important to realize that algorithms do not, in themselves, decide mathematical truth. The validity of an algorithm must always be established by external means.

<== попередня сторінка	\|	наступна сторінка ==>
Professionally oriented texts for individual	\|	Text 3. Construction of the Mandelbrot Set

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.008 сек.